Loss Models: From Data to Decisions, 4th Edition

9.1 Introduction

An insurance enterprise exists because of its ability to pool risks. By insuring many people, the individual risks are combined into an aggregate risk that is manageable and can be priced at a level that will attract customers. Consider the following simple example.

EXAMPLE 9.1

An insurable event has a 10% probability of occurring and when it occurs results in a loss of 5,000. Market research has indicated that consumers will pay at most 550 to purchase insurance against this event. How many policies must a company sell in order to have a 95% chance of making money (ignoring expenses)?

Let n be the number of policies sold. A reasonable model for the number of claims, C is a binomial distribution with m = n and q = 0.1 and the total paid will be 5,000C.

To achieve the desired outcome,

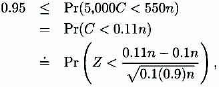
where the approximation uses the Central Limit Theorem, With the normal distribution

which gives the answer n = 3,457.44, and so at least 3,458 policies must be sold.

The goal of this chapter is to build a model for the total payments by an insurance system (which may be the entire company, a line of business, those covered by a group insurance contract, or even a single policy). The ...