Below, is our basic composition operation.
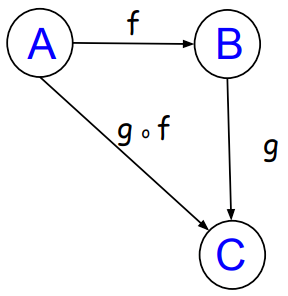
The composition operation is g o f, g after f applies arg x (from A) to give us g applied to f applied to x: (g o f)(x) = g(f(x)).
If f(g(x)) = g(f(x)) for all x, then we can say that f and g commute under composition.
However, that's not typical. Function composition is generally not commutative.
Let's take an example. Remember when we composed f(x) = x + 2 with g(x) = x2 + 1 earlier in the chapter? We solved g(f(1)) = 10, but what about f(g(1))? Does that also equal 10? Let's see now:
g(1) = 12 + 1 = 2 and f(2) = 4
So, no, our functions f and g are not associative: g(f(1)) ...
