Künstliche Intelligenz im Finanzwesen

Kapitel 1. Künstliche Intelligenz

Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: [e-mail]

Es ist das erste Mal, dass ein Computerprogramm einen menschlichen Profispieler in einem Go-Spiel in voller Größe besiegt hat - eine Leistung, von der man bisher dachte, dass sie mindestens ein Jahrzehnt entfernt ist.

David Silver et al. (2016)

In diesem Kapitel werden allgemeine Begriffe, Ideen und Definitionen aus dem Bereich der künstlichen Intelligenz (KI) für die Zwecke dieses Buches eingeführt. Außerdem enthält es ausgearbeitete Beispiele für verschiedene Arten von wichtigen Lernalgorithmen. Das Kapitel "Algorithmen" nimmt eine breite Perspektive ein und kategorisiert Datenarten, Lerntypen und Problemtypen, die typischerweise in einem KI-Kontext auftreten. In diesem Kapitel werden auch Beispiele für unüberwachtes und verstärkendes Lernen vorgestellt. " Neuronale Netze" führt direkt in die Welt der neuronalen Netze ein, die nicht nur für die folgenden Kapitel des Buches von zentraler Bedeutung sind, sondern sich auch als einer der leistungsstärksten Algorithmen erwiesen haben, die die KI heutzutage zu bieten hat. In "Die Bedeutung von Daten" geht es um die Bedeutung von Datenvolumen und -vielfalt im Zusammenhang mit KI.

Algorithmen

In diesem Abschnitt werden grundlegende Begriffe aus dem Bereich der KI vorgestellt, die für dieses Buch relevant sind. Es werden die verschiedenen Arten von Daten, Lernen, Problemen und Ansätzen erörtert, die unter dem allgemeinen Begriff KI subsumiert werden können. Alpaydin (2016) bietet eine informelle Einführung und einen Überblick über viele der Themen, die in diesem Abschnitt nur kurz behandelt werden, sowie viele Beispiele.

Arten von Daten

Daten haben im Allgemeinen zwei Hauptkomponenten:

Eigenschaften

Merkmalsdaten (oder Eingabedaten) sind Daten, die als Eingabe für einen Algorithmus dienen. In einem finanziellen Kontext könnten das zum Beispiel das Einkommen und die Ersparnisse eines potenziellen Schuldners sein.

Etiketten

Markierungsdaten (oder Ausgabedaten) sind Daten, die als relevante Ausgabe angegeben werden, die z. B. von einem überwachten Lernalgorithmus gelernt werden soll. In einem finanziellen Kontext könnte dies die Kreditwürdigkeit eines potenziellen Schuldners sein.

Arten des Lernens

Es gibt drei Haupttypen von Lernalgorithmen:

Überwachtes Lernen (SL)

Das sind Algorithmen, die aus einem gegebenen Musterdatensatz von Merkmalen (Eingabe) und Kennzeichnungen (Ausgabe) lernen. Im nächsten Abschnitt werden Beispiele für solche Algorithmen vorgestellt, wie die gewöhnliche Kleinstquadrat-Regression (OLS) und neuronale Netze. Das Ziel des überwachten Lernens ist es, die Beziehung zwischen den Eingabe- und Ausgabewerten zu lernen. Im Finanzwesen könnten solche Algorithmen trainiert werden, um vorherzusagen, ob ein potenzieller Schuldner kreditwürdig ist oder nicht. Für die Zwecke dieses Buches sind dies die wichtigsten Arten von Algorithmen.

Unüberwachtes Lernen (UL)

Das sind Algorithmen, die nur aus einem bestimmten Musterdatensatz von Merkmalen (Eingabewerten) lernen, oft mit dem Ziel, eine Struktur in den Daten zu finden. Sie sollen etwas über den Eingabedatensatz lernen, wenn sie z. B. einige Leitparameter haben. Clustering-Algorithmen fallen in diese Kategorie. Im Finanzkontext können solche Algorithmen Aktien in bestimmte Gruppen einteilen.

Verstärkungslernen (RL)

Das sind Algorithmen, die durch Versuch und Irrtum lernen, indem sie eine Belohnung für eine Aktion erhalten. Je nachdem, welche Belohnungen und Bestrafungen sie erhalten, aktualisieren sie eine optimale Handlungsstrategie. Solche Algorithmen werden z. B. in Umgebungen eingesetzt, in denen ständig Aktionen ausgeführt werden müssen und Belohnungen sofort erhalten werden, wie z. B. in einem Computerspiel.

Da das überwachte Lernen im folgenden Abschnitt detailliert behandelt wird, werden kurze Beispiele das unüberwachte Lernen und das Verstärkungslernen veranschaulichen.

Unüberwachtes Lernen

Einfach ausgedrückt, sortiert ein k-means Clustering-Algorithmus $n$ Beobachtungen in $k$ Jede Beobachtung gehört zu dem Cluster, zu dem ihr Mittelwert (Zentrum) am nächsten liegt. Der folgende Python-Code erzeugt Beispieldaten, für die die Merkmalsdaten geclustert werden. Abbildung 1-1 visualisiert die geclusterten Beispieldaten und zeigt auch, dass der hier verwendete scikit-learn KMeans Algorithmus die Cluster perfekt identifiziert hat. Die Färbung der Punkte basiert auf dem, was der Algorithmus gelernt hat.¹

In [1]: import numpy as np
        import pandas as pd
        from pylab import plt, mpl
        plt.style.use('seaborn')
        mpl.rcParams['savefig.dpi'] = 300
        mpl.rcParams['font.family'] = 'serif'
        np.set_printoptions(precision=4, suppress=True)

In [2]: from sklearn.cluster import KMeans
        from sklearn.datasets import make_blobs

In [3]: x, y = make_blobs(n_samples=100, centers=4,
                          random_state=500, cluster_std=1.25)  

In [4]: model = KMeans(n_clusters=4, random_state=0)  

In [5]: model.fit(x)  
Out[5]: KMeans(n_clusters=4, random_state=0)

In [6]: y_ = model.predict(x)  

In [7]: y_  
Out[7]: array([3, 3, 1, 2, 1, 1, 3, 2, 1, 2, 2, 3, 2, 0, 0, 3, 2, 0, 2, 0, 0, 3,
               1, 2, 1, 1, 0, 0, 1, 3, 2, 1, 1, 0, 1, 3, 1, 3, 2, 2, 2, 1, 0, 0,
               3, 1, 2, 0, 2, 0, 3, 0, 1, 0, 1, 3, 1, 2, 0, 3, 1, 0, 3, 2, 3, 0,
               1, 1, 1, 2, 3, 1, 2, 0, 2, 3, 2, 0, 2, 2, 1, 3, 1, 3, 2, 2, 3, 2,
               0, 0, 0, 3, 3, 3, 3, 0, 3, 1, 0, 0], dtype=int32)

In [8]: plt.figure(figsize=(10, 6))
        plt.scatter(x[:, 0], x[:, 1], c=y_,  cmap='coolwarm');

Es wird ein Beispieldatensatz mit geclusterten Merkmalsdaten erstellt.

Ein KMeans Modellobjekt wird instanziiert und die Anzahl der Cluster festgelegt.

Das Modell wird an die Merkmalsdaten angepasst.

Die Vorhersagen werden anhand des angepassten Modells erstellt.

Die Vorhersagen sind Zahlen von 0 bis 3, die jeweils für ein Cluster stehen.

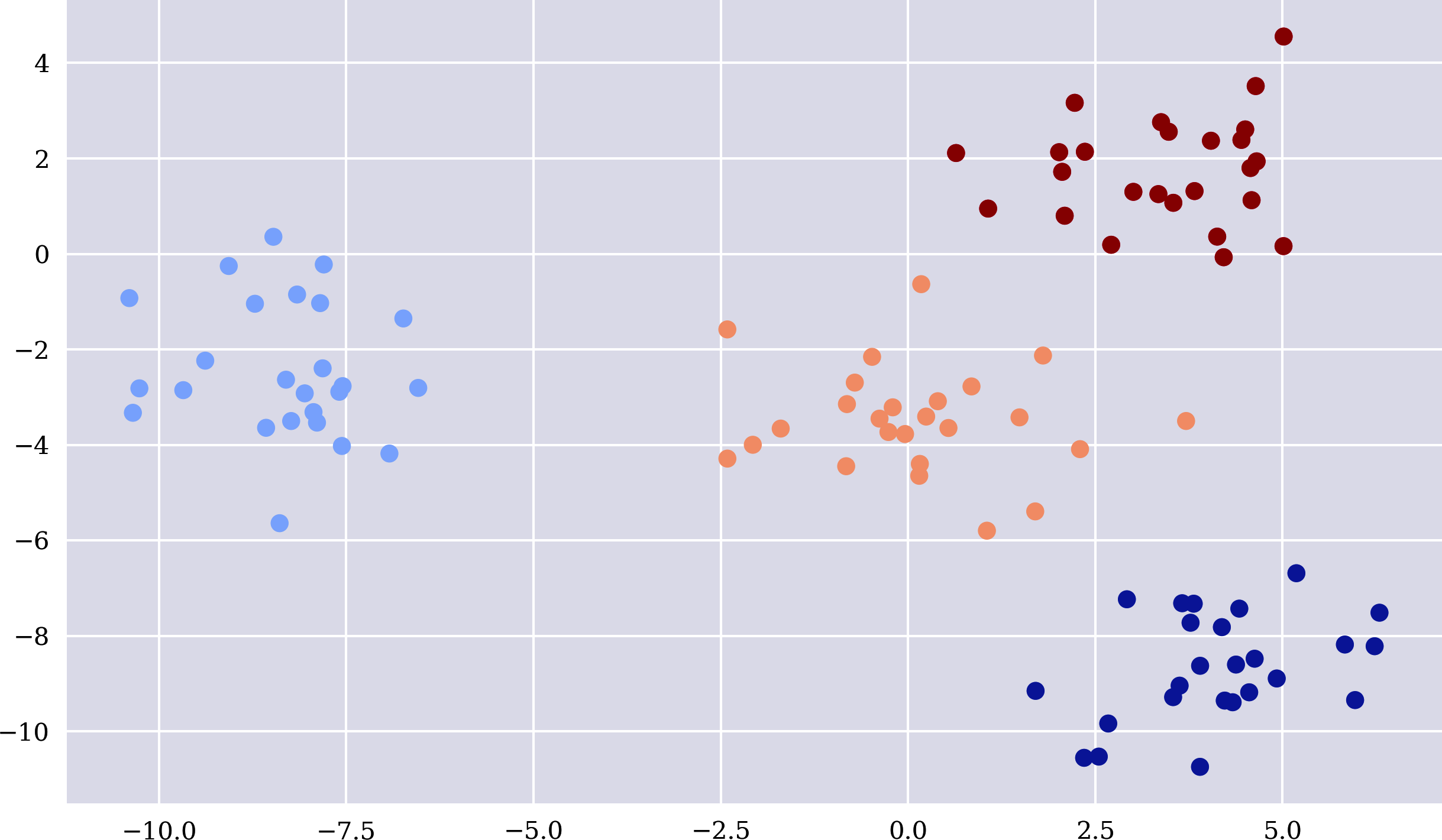
Abbildung 1-1. Unüberwachtes Lernen von Clustern

Sobald ein Algorithmus wie KMeans trainiert ist, kann er zum Beispiel das Cluster für eine neue (noch nicht gesehene) Kombination von Merkmalswerten vorhersagen. Nehmen wir an, ein solcher Algorithmus wird auf Merkmalsdaten trainiert, die potenzielle und tatsächliche Schuldner einer Bank beschreiben. Er könnte durch die Bildung von zwei Clustern etwas über die Kreditwürdigkeit potenzieller Schuldner lernen. Neue potenzielle Schuldner können dann in ein bestimmtes Cluster einsortiert werden: "kreditwürdig" versus "nicht kreditwürdig".

Verstärkungslernen

Das folgende Beispiel basiert auf einem Münzwurfspiel, das mit einer Münze gespielt wird, die in 80 % der Fälle auf Kopf und in 20 % der Fälle auf Zahl fällt. Das Münzwurfspiel ist stark verzerrt, um die Vorteile des Lernens im Vergleich zu einem uninformierten Basisalgorithmus hervorzuheben. Der Basisalgorithmus, der nach dem Zufallsprinzip wettet und gleichmäßig auf Kopf und Zahl verteilt, erzielt pro Epoche von 100 gespielten Wetten im Durchschnitt eine Gesamtbelohnung von etwa 50:

In [9]: ssp = [1, 1, 1, 1, 0]  

In [10]: asp = [1, 0]  

In [11]: def epoch():
             tr = 0
             for _ in range(100):
                 a = np.random.choice(asp)  
                 s = np.random.choice(ssp)  
                 if a == s:
                     tr += 1  
             return tr

In [12]: rl = np.array([epoch() for _ in range(15)])  
         rl
Out[12]: array([53, 55, 50, 48, 46, 41, 51, 49, 50, 52, 46, 47, 43, 51, 52])

In [13]: rl.mean()  
Out[13]: 48.93333333333333

Der Zustandsraum (1 = Kopf, 0 = Zahl).

Der Aktionsraum (1 = Wette auf Kopf, 0 = Wette auf Zahl).

Eine Aktion wird zufällig aus dem Aktionsraum ausgewählt.

Ein Zustand wird zufällig aus dem Zustandsraum ausgewählt.

Der Gesamtgewinn tr wird um eins erhöht, wenn die Wette richtig ist.

Das Spiel wird über eine Anzahl von Epochen gespielt; jede Epoche umfasst 100 Einsätze.

Die durchschnittliche Gesamtbelohnung der gespielten Epochen wird berechnet.

Beim Verstärkungslernen wird versucht, aus dem zu lernen, was nach der Ausführung einer Handlung beobachtet wird, in der Regel auf der Grundlage einer Belohnung. Der Einfachheit halber merkt sich der folgende Lernalgorithmus die Zustände, die in jeder Runde beobachtet werden, nur insofern, als sie an das Objekt des Aktionsraums list angehängt werden. Auf diese Weise lernt der Algorithmus die Verzerrungen im Spiel, wenn auch vielleicht nicht perfekt. Durch die zufällige Auswahl aus dem aktualisierten Aktionsraum wird die Voreingenommenheit widergespiegelt, da die Wette natürlich häufiger Kopf sein wird. Im Laufe der Zeit wird im Durchschnitt in etwa 80 % der Fälle Kopf gewählt. Die durchschnittliche Gesamtbelohnung von etwa 65 spiegelt die Verbesserung des Lernalgorithmus im Vergleich zum uninformierten Basisalgorithmus wider:

In [14]: ssp = [1, 1, 1, 1, 0]

In [15]: def epoch():
             tr = 0
             asp = [0, 1]  
             for _ in range(100):
                 a = np.random.choice(asp)
                 s = np.random.choice(ssp)
                 if a == s:
                     tr += 1
                 asp.append(s)  
             return tr


In [16]: rl = np.array([epoch() for _ in range(15)])
         rl
Out[16]: array([64, 65, 77, 65, 54, 64, 71, 64, 57, 62, 69, 63, 61, 66, 75])

In [17]: rl.mean()
Out[17]: 65.13333333333334

Setzt den Aktionsraum vor dem Start zurück (over)

Fügt den beobachteten Zustand zum Aktionsraum hinzu

Arten von Aufgaben

Je nach Art der Etikettendaten und der Aufgabenstellung sind zwei Arten von Aufgaben wichtig, die gelernt werden müssen:

Schätzung

Schätzung (oder Annäherung, Regression) bezieht sich auf die Fälle, in denen die Beschriftungsdaten reellwertig (kontinuierlich) sind, d.h. sie werden technisch als Fließkommazahlen dargestellt.

Klassifizierung

Klassifizierung bezieht sich auf die Fälle, in denen die Kennzeichnungsdaten aus einer endlichen Anzahl von Klassen oder Kategorien bestehen, die in der Regel durch diskrete Werte (positive natürliche Zahlen) dargestellt werden, die ihrerseits technisch als ganze Zahlen dargestellt werden.

Im folgenden Abschnitt findest du Beispiele für beide Arten von Aufgaben.

Arten von Ansätzen

Bevor wir diesen Abschnitt abschließen, sollten wir noch einige Definitionen vornehmen. Dieses Buch folgt der gängigen Unterscheidung zwischen den folgenden drei Hauptbegriffen:

Künstliche Intelligenz (KI)

KI umfasst alle Arten des Lernens (Algorithmen), wie zuvor definiert, und einige mehr (zum Beispiel Expertensysteme).

Maschinelles Lernen (ML)

ML ist die Disziplin des Lernens von Zusammenhängen und anderen Informationen über gegebene Datensätze auf der Grundlage eines Algorithmus und eines Erfolgsmaßes. Ein Erfolgsmaß könnte zum Beispiel der mittlere quadratische Fehler (MSE) sein, der sich aus den zu schätzenden Werten der Labels und der Ausgabewerte sowie den vom Algorithmus vorhergesagten Werten ergibt. ML ist ein Teilbereich der KI.

Deep Learning (DL)

DL umfasst alle Algorithmen, die auf neuronalen Netzen basieren. Der Begriff "deep" wird normalerweise nur verwendet, wenn das neuronale Netz mehr als eine versteckte Schicht hat. DL ist ein Teilbereich des maschinellen Lernens und damit auch ein Teilbereich der KI.

DL hat sich für eine Reihe von Problembereichen als nützlich erwiesen. Sie eignet sich sowohl für Schätz- und Klassifizierungsaufgaben als auch für RL. In vielen Fällenschneiden DL-basierte Ansätze besserab als alternative Algorithmen wie die logistische Regression oder kernelbasierte Algorithmen wie Support Vector Machines.² Deshalb konzentriert sich dieses Buch hauptsächlich auf DL. Zu den verwendeten DL-Ansätzen gehören dichte neuronale Netze (DNNs), rekurrente neuronale Netze (RNNs) und Faltungsneuronale Netze (CNNs). Mehr Details dazu findest du in späteren Kapiteln, insbesondere in Teil III.

Neuronale Netze

Die vorherigen Abschnitte geben einen Überblick über die Algorithmen in der KI. Dieser Abschnitt zeigt, wie sich neuronale Netze einfügen. Ein einfaches Beispiel soll veranschaulichen, was neuronale Netze im Vergleich zu traditionellen statistischen Methoden wie der gewöhnlichen Kleinstquadratregression (OLS) auszeichnet. Das Beispiel beginnt mit Mathematik und verwendet dann die lineare Regression zur Schätzung (oder Funktionsannäherung) und wendet schließlich neuronale Netze an, um die Schätzung durchzuführen. Der hier gewählte Ansatz ist ein überwachtes Lernen, bei dem die Aufgabe darin besteht, Bezeichnungen anhand von Merkmalsdaten zu schätzen. Dieser Abschnitt veranschaulicht auch die Verwendung neuronaler Netze im Zusammenhang mitKlassifizierungsproblemen.

OLS-Regression

Angenommen, eine mathematische Funktion ist wie folgt gegeben:

$$f:ℝ\to ℝ,y=2x^2-\frac{1}{3}{x}^3$$

Eine solche Funktion wandelt einen Eingabewert $x$ in einen Ausgangswert $y$. Oder sie wandelt eine Reihe von Eingabewerten um $x_1,x_2,...,x_N$ in eine Reihe von Ausgangswerten $y_1,y_2,...,y_N$. Der folgende Python-Code implementiert die mathematische Funktion als Python-Funktion und erzeugt eine Reihe von Eingabe- und Ausgabewerten. In Abbildung 1-2 werden die Ausgabewerte gegen die Eingabewerte aufgetragen:

In [18]: def f(x):
             return 2 * x ** 2 - x ** 3 / 3  

In [19]: x = np.linspace(-2, 4, 25)  
         x  
Out[19]: array([-2.  , -1.75, -1.5 , -1.25, -1.  , -0.75, -0.5 , -0.25,  0.  ,
                 0.25,  0.5 ,  0.75,  1.  ,  1.25,  1.5 ,  1.75,  2.  ,  2.25,
                 2.5 ,  2.75,  3.  ,  3.25,  3.5 ,  3.75,  4.  ])

In [20]: y = f(x)  
         y  
Out[20]: array([10.6667,  7.9115,  5.625 ,  3.776 ,  2.3333,  1.2656,  0.5417,
                 0.1302,  0.    ,  0.1198,  0.4583,  0.9844,  1.6667,  2.474 ,
                 3.375 ,  4.3385,  5.3333,  6.3281,  7.2917,  8.1927,  9.    ,
                 9.6823, 10.2083, 10.5469, 10.6667])

In [21]: plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro');

Die mathematische Funktion als Python-Funktion

Die Eingabewerte

Die Ausgangswerte

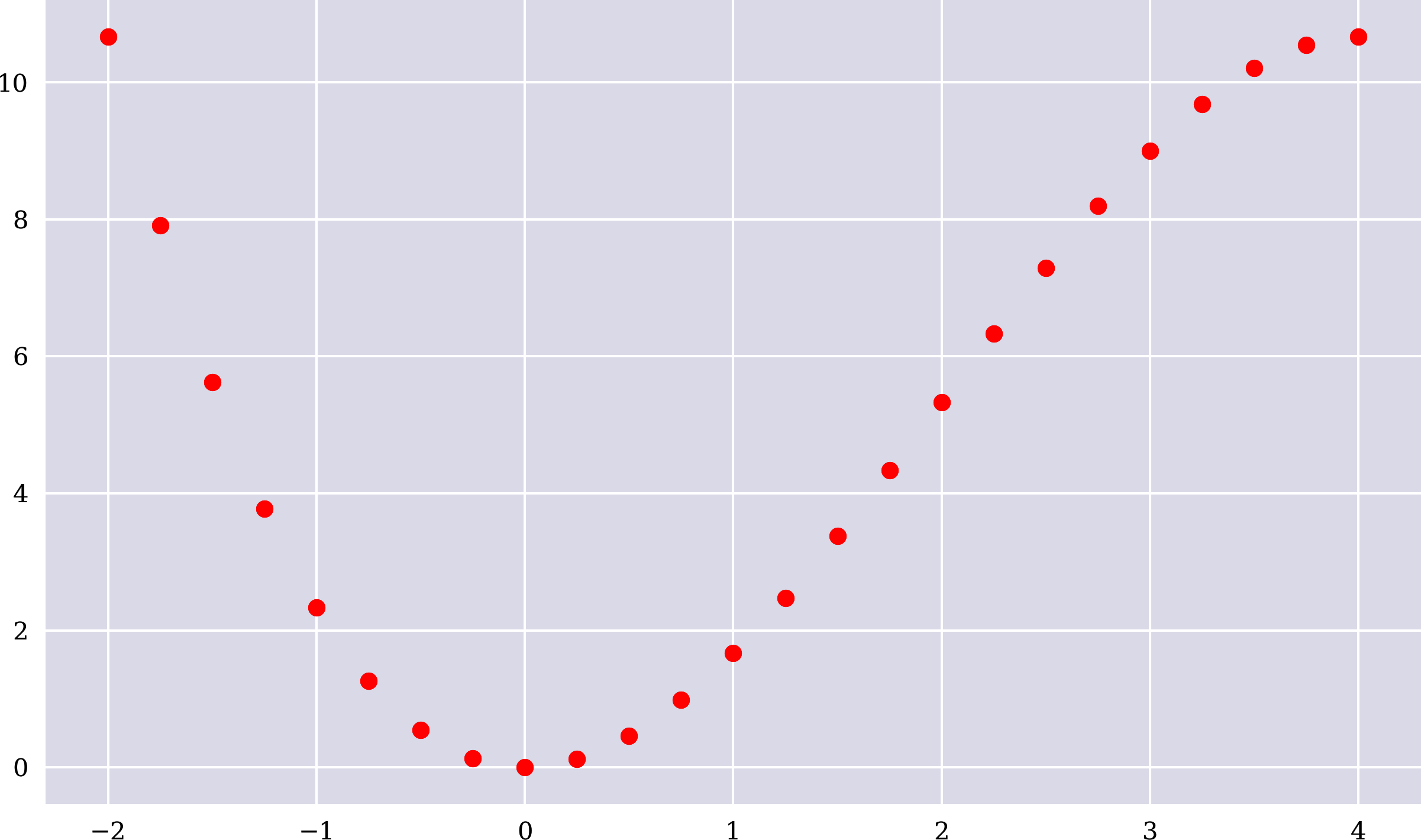
Abbildung 1-2. Ausgangswerte gegen Eingangswerte

Während im mathematischen Beispiel die Funktion an erster Stelle steht, die Eingabedaten an zweiter und die Ausgabedaten an dritter Stelle, ist die Reihenfolge beimstatistischen Lernen anders. Nehmen wir an, dass die vorherigen Eingabewerte und Ausgabewerte gegeben sind. Sie stellen die Stichprobe (Daten) dar. Das Problem bei der statistischen Regression besteht darin, eine Funktion zu finden, die die funktionale Beziehung zwischen den Eingabewerten (auch unabhängige Werte genannt) und den Ausgabewerten (auch abhängige Werte genannt) so gut wie möglich annähert.

Nehmen wir eine einfache lineare OLS-Regression an. In diesem Fall wird angenommen, dass die funktionale Beziehung zwischen den Eingangs- und Ausgangswerten linear ist, und das Problem besteht darin, optimale Parameter zu finden $\alpha$ und $\beta$ für die folgende lineare Gleichung zu finden:

$$\widehat{f}:ℝ\to ℝ,\widehat{y}=\alpha +\beta x$$

Für gegebene Eingabewerte $x_1,x_2,...,x_N$ und Ausgangswerte $y_1,y_2,...,y_N$optimal bedeutet in diesem Fall, dass sie den mittleren quadratischen Fehler (MSE) zwischen den realen Ausgangswerten und den approximierten Ausgangswerten minimieren:

$$\underset{\alpha ,\beta }{min}\frac{1}{N}\sum _n^N{\left(y_n-\widehat{f}\left(x_n\right)\right)}^2$$

Für den Fall einer einfachen linearen Regression ist die Lösung $({\alpha }^{*},{\beta }^{*})$ ist in geschlossener Form bekannt, wie in der folgenden Gleichung dargestellt. Die Balken auf den Variablen geben die Mittelwerte der Stichprobe an:

$$\begin{array}{ccc}{\beta }^{*}& =& \frac{Cov(x,y)}{Var\left(x\right)}\\ {\alpha }^{*}& =& \overline{y}-\beta \overline{x}\end{array}$$

Der folgende Python-Code berechnet die optimalen Parameterwerte, schätzt (approximiert) die Ausgangswerte linear und stellt die lineare Regressionslinie neben den Beispieldaten dar (siehe Abbildung 1-3). Der Ansatz der linearen Regression funktioniert hier bei der Annäherung an die funktionale Beziehung nicht besonders gut. Dies wird durch den relativ hohen MSE-Wert bestätigt:

In [22]: beta = np.cov(x, y, ddof=0)[0, 1] / np.var(x)  
         beta  
Out[22]: 1.0541666666666667

In [23]: alpha = y.mean() - beta * x.mean()  
         alpha  
Out[23]: 3.8625000000000003

In [24]: y_ = alpha + beta * x  

In [25]: MSE = ((y - y_) ** 2).mean()  
         MSE  
Out[25]: 10.721953125

In [26]: plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro', label='sample data')
         plt.plot(x, y_, lw=3.0, label='linear regression')
         plt.legend();

Berechnung der optimalen $\beta$

Berechnung der optimalen $\alpha$

Berechnung der geschätzten Ausgangswerte

Berechnung des MSE bei der Approximation

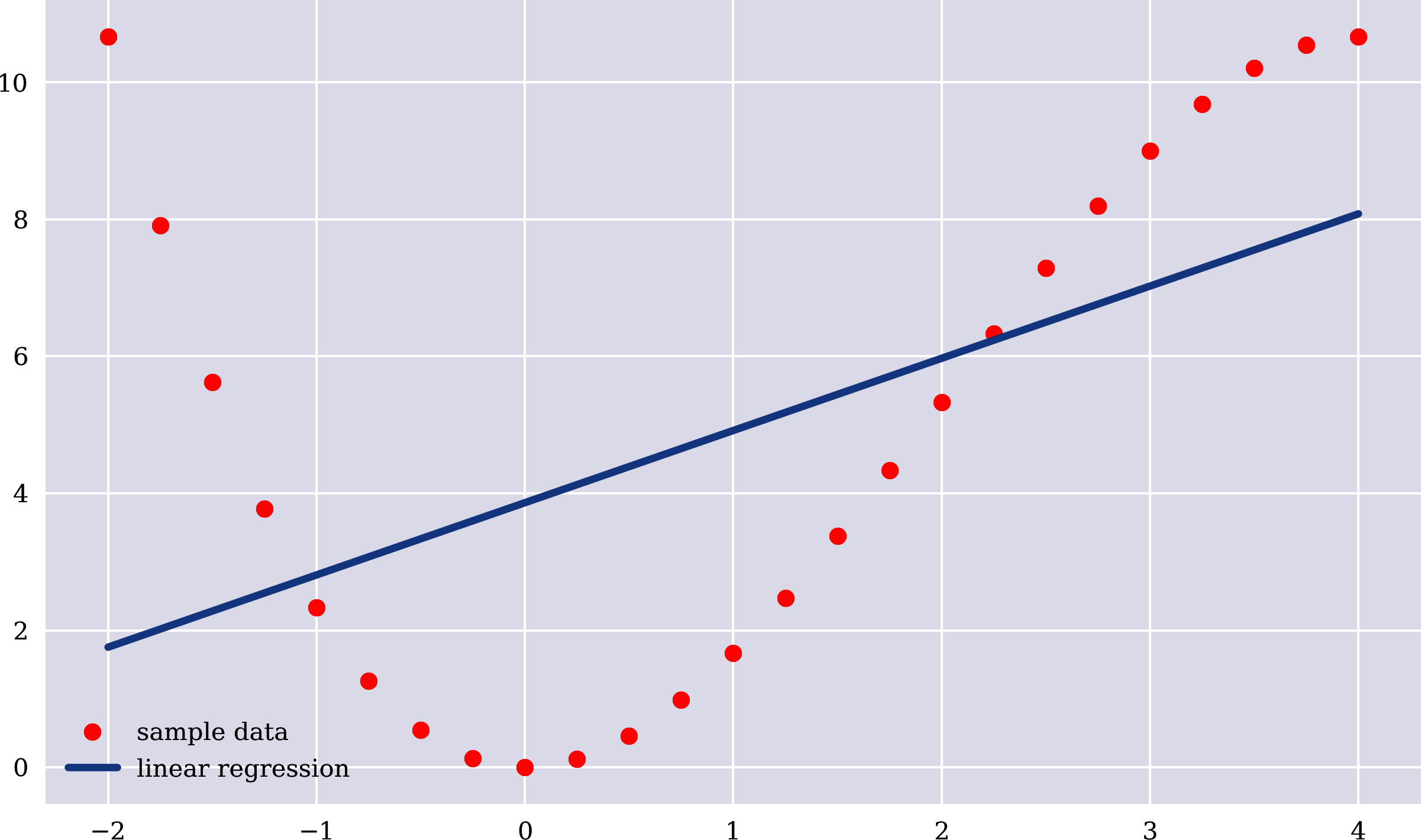
Abbildung 1-3. Beispieldaten und lineare Regressionslinie

Wie kann der MSE-Wert verbessert (verringert) werden - vielleicht sogar auf 0, d. h. auf eine "perfekte Schätzung"? Natürlich ist die OLS-Regression nicht auf eine einfache lineare Beziehung beschränkt. Zusätzlich zu den konstanten und linearen Termen können z. B. auch Monome höherer Ordnung als Basisfunktionen hinzugefügt werden. Vergleiche dazu die Regressionsergebnisse in Abbildung 1-4 und den folgenden Code, der die Abbildung erstellt. Die Verbesserungen, die sich durch die Verwendung quadratischer und kubischer Monome als Basisfunktionen ergeben, sind offensichtlich und werden durch die berechneten MSE-Werte auch numerisch bestätigt. Für Basisfunktionen bis einschließlich des kubischen Monoms ist die Schätzung perfekt und die funktionale Beziehung wird perfekt wiederhergestellt:

In [27]: plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro', label='sample data')
         for deg in [1, 2, 3]:
             reg = np.polyfit(x, y, deg=deg)  
             y_ = np.polyval(reg, x)  
             MSE = ((y - y_) ** 2).mean()  
             print(f'deg={deg} | MSE={MSE:.5f}')
             plt.plot(x, np.polyval(reg, x), label=f'deg={deg}')
         plt.legend();
         deg=1 | MSE=10.72195
         deg=2 | MSE=2.31258
         deg=3 | MSE=0.00000

In [28]: reg  
Out[28]: array([-0.3333,  2.    ,  0.    , -0.    ])

Regressionsschritt

Annäherungsschritt

MSE-Berechnung

Optimale ("perfekte") Parameterwerte

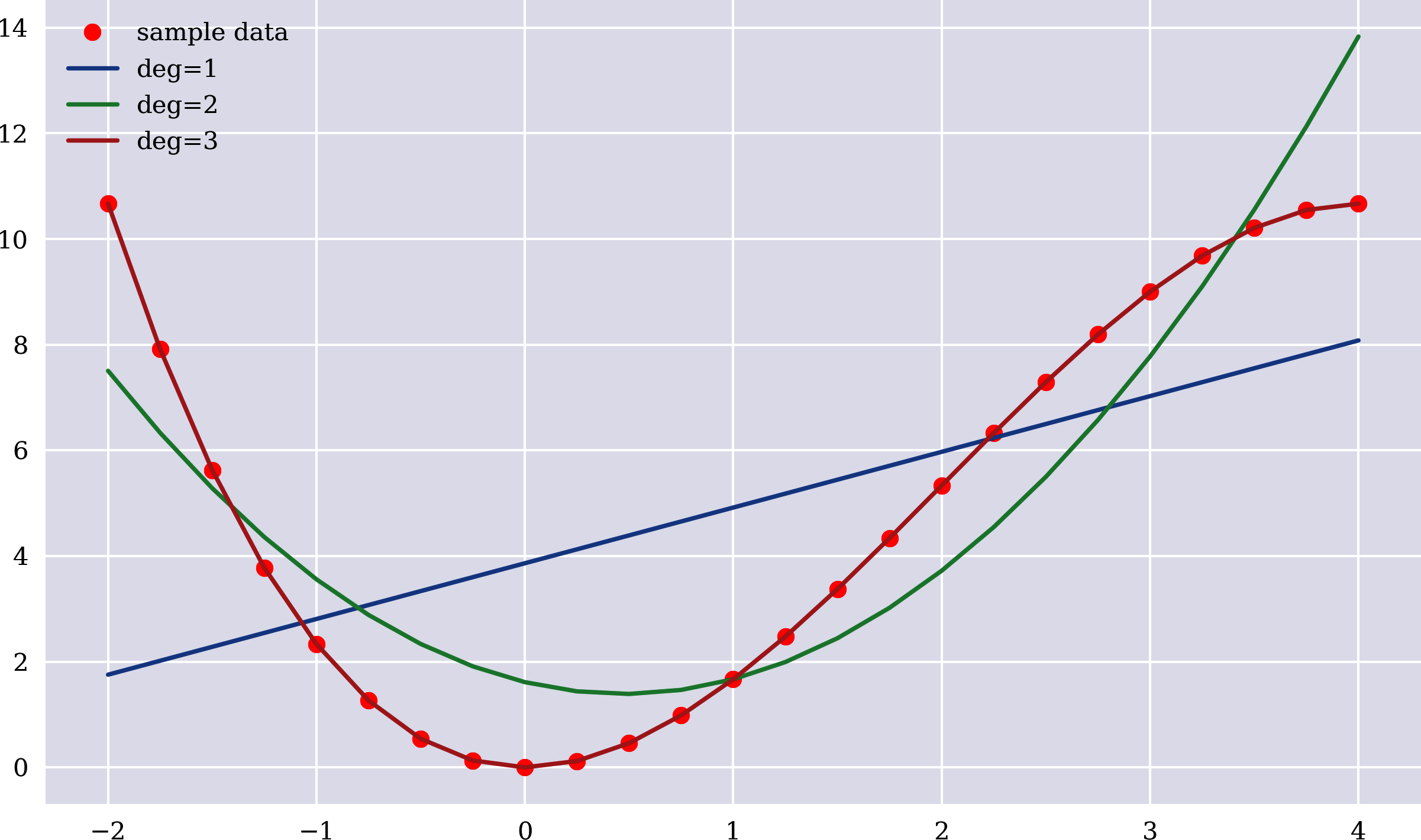
Abbildung 1-4. Beispieldaten und OLS-Regressionslinien

Wenn man das Wissen über die Form der zu approximierenden mathematischen Funktion nutzt und entsprechend mehr Basisfunktionen zur Regression hinzufügt, führt dies zu einer "perfekten Approximation". Das bedeutet, dass die OLS-Regression die genauen Faktoren des quadratischen bzw. kubischen Teils der ursprünglichen Funktion wiederherstellt.

Schätzung mit neuronalen Netzen

Aber nicht alle Beziehungen sind von dieser Art. Hier können z. B. neuronale Netze helfen. Ohne ins Detail zu gehen, können neuronale Netze eine Vielzahl von funktionalen Beziehungen annähern. Das Wissen über die Form der Beziehung ist in der Regel nicht erforderlich.

Scikit-learn

Der folgende Python-Code verwendet die Klasse MLPRegressor von scikit-learn, die ein DNN zur Schätzung implementiert. DNNs werden manchmal auch als Multi-Layer Perceptron (MLP) bezeichnet.³ Die Ergebnisse sind nicht perfekt, wie Abbildung 1-5 und der MSE zeigen. Allerdings sind sie für die verwendete einfache Konfiguration schon recht gut:

In [29]: from sklearn.neural_network import MLPRegressor

In [30]: model = MLPRegressor(hidden_layer_sizes=3 * [256],
                              learning_rate_init=0.03,
                              max_iter=5000)  

In [31]: model.fit(x.reshape(-1, 1), y)  
Out[31]: MLPRegressor(hidden_layer_sizes=[256, 256, 256], learning_rate_init=0.03,
                      max_iter=5000)

In [32]: y_ = model.predict(x.reshape(-1, 1))  

In [33]: MSE = ((y - y_) ** 2).mean()
         MSE
Out[33]: 0.021662355744355866

In [34]: plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro', label='sample data')
         plt.plot(x, y_, lw=3.0, label='dnn estimation')
         plt.legend();

Instanziiert das MLPRegressor Objekt

Führt den Anpassungs- oder Lernschritt durch

Implementiert den Schritt der Vorhersage

Wenn man sich die Ergebnisse in Abbildung 1-4 und Abbildung 1-5 ansieht, könnte man annehmen, dass sich die Methoden und Ansätze gar nicht so sehr unterscheiden. Es gibt jedoch einen grundlegenden Unterschied, der hervorzuheben ist. Während der OLS-Regressionsansatz, wie er explizit für die einfache lineare Regression gezeigt wird, auf der Berechnung bestimmter, genau festgelegter Größen und Parameter beruht, stützt sich der Ansatz des neuronalen Netzes auf inkrementelles Lernen. Das wiederum bedeutet, dass eine Reihe von Parametern, die Gewichte innerhalb des neuronalen Netzes, zunächst nach dem Zufallsprinzip initialisiert und dann schrittweise anhand der Unterschiede zwischen dem Ausgang des neuronalen Netzes und den Ausgangswerten der Stichprobe angepasst werden. Mit diesem Ansatz kannst du ein neuronales Netz schrittweise neu trainieren (aktualisieren).

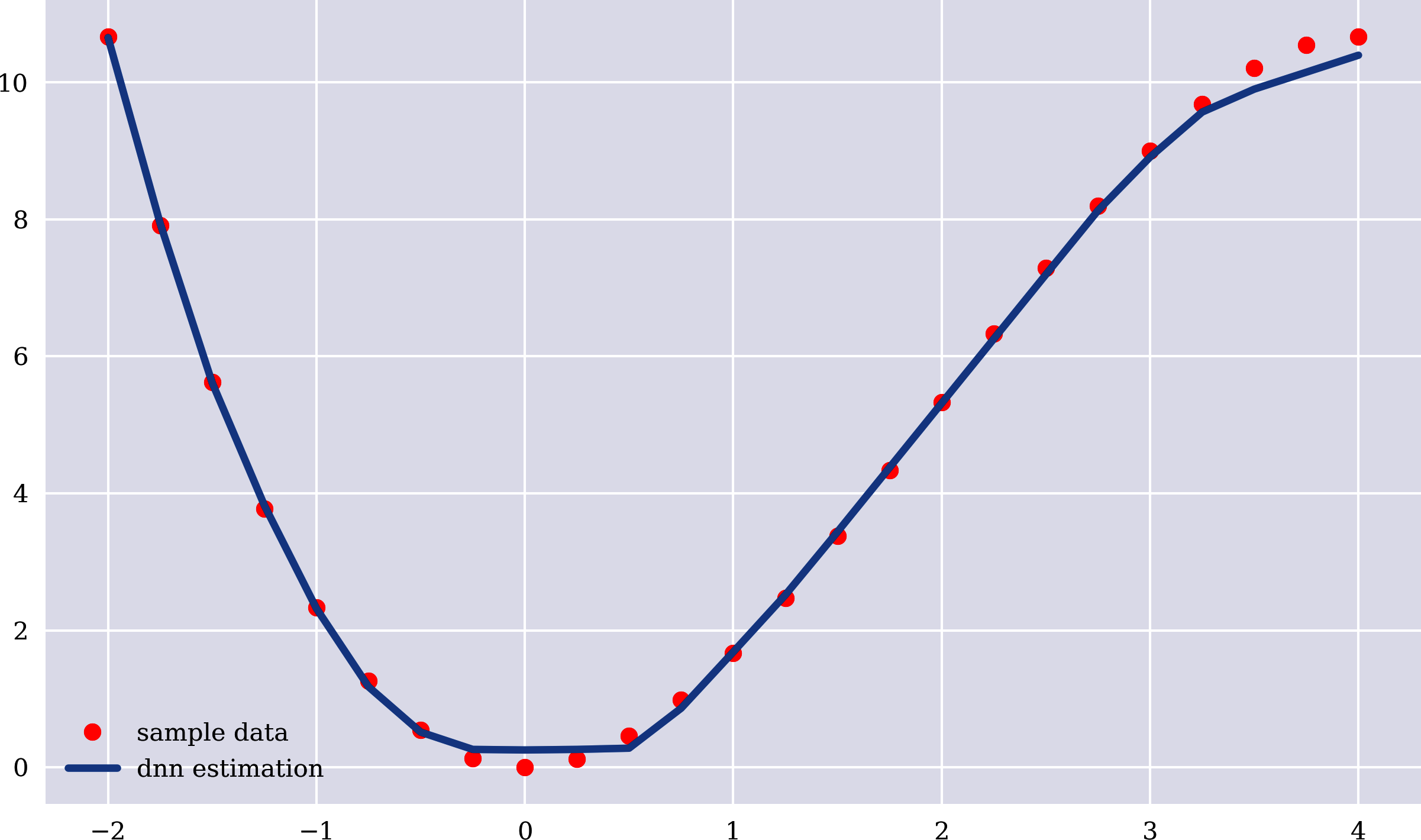
Abbildung 1-5. Beispieldaten und auf dem neuronalen Netz basierende Schätzungen

Keras

Das nächste Beispiel verwendet ein sequentielles Modell mit dem Deep-Learning-Paket Keras.⁴ Das Modell wird für 100 Epochen angepasst bzw. trainiert. Das Verfahren wird für fünf Runden wiederholt. Nach jeder dieser Runden wird die Annäherung durch das neuronale Netz aktualisiert und aufgezeichnet. Abbildung 1-6 zeigt, wie sich die Annäherung mit jeder Runde allmählich verbessert. Das spiegelt sich auch in den sinkenden MSE-Werten wider. Das Endergebnis ist zwar nicht perfekt, aber angesichts der Einfachheit des Modells ist es recht gut:

In [35]: import tensorflow as tf
         tf.random.set_seed(100)

In [36]: from keras.layers import Dense
         from keras.models import Sequential
         Using TensorFlow backend.

In [37]: model = Sequential()  
         model.add(Dense(256, activation='relu', input_dim=1)) 
         model.add(Dense(1, activation='linear'))  
         model.compile(loss='mse', optimizer='rmsprop')  

In [38]: ((y - y_) ** 2).mean()
Out[38]: 0.021662355744355866

In [39]: plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro', label='sample data')
         for _ in range(1, 6):
             model.fit(x, y, epochs=100, verbose=False)  
             y_ =  model.predict(x)  
             MSE = ((y - y_.flatten()) ** 2).mean()  
             print(f'round={_} | MSE={MSE:.5f}')
             plt.plot(x, y_, '--', label=f'round={_}')  
         plt.legend();
         round=1 | MSE=3.09714
         round=2 | MSE=0.75603
         round=3 | MSE=0.22814
         round=4 | MSE=0.11861
         round=5 | MSE=0.09029

Instanziiert das Sequential Modellobjekt

Fügt eine dicht verknüpfte versteckte Schicht mit gleichgerichteter linearer Einheit (ReLU ) hinzu⁵

Fügt die Ausgabeschicht mit linearer Aktivierung hinzu

Kompiliert das Modell für die Verwendung

Trainiert das neuronale Netz für eine feste Anzahl von Epochen

Implementiert den Schritt der Annäherung

Berechnet den aktuellen MSE

Stellt die aktuellen Näherungsergebnisse dar

Grob gesagt, kann man sagen, dass das neuronale Netz bei der Schätzung fast genauso gut abschneidet wie die OLS-Regression, die ein perfektes Ergebnis liefert. Warum also überhaupt neuronale Netze verwenden? Eine umfassendere Antwort wird vielleicht später in diesem Buch gegeben, aber ein etwas anderes Beispiel könnte einen Hinweis darauf geben.

Betrachte stattdessen den vorherigen Beispieldatensatz, der aus einer wohldefinierten mathematischen Funktion generiert wurde, nun als einen zufälligen Beispieldatensatz, für den sowohl die Merkmale als auch die Bezeichnungen zufällig ausgewählt werden. Natürlich dient dieses Beispiel nur der Veranschaulichung und lässt keine tiefgreifende Interpretation zu.

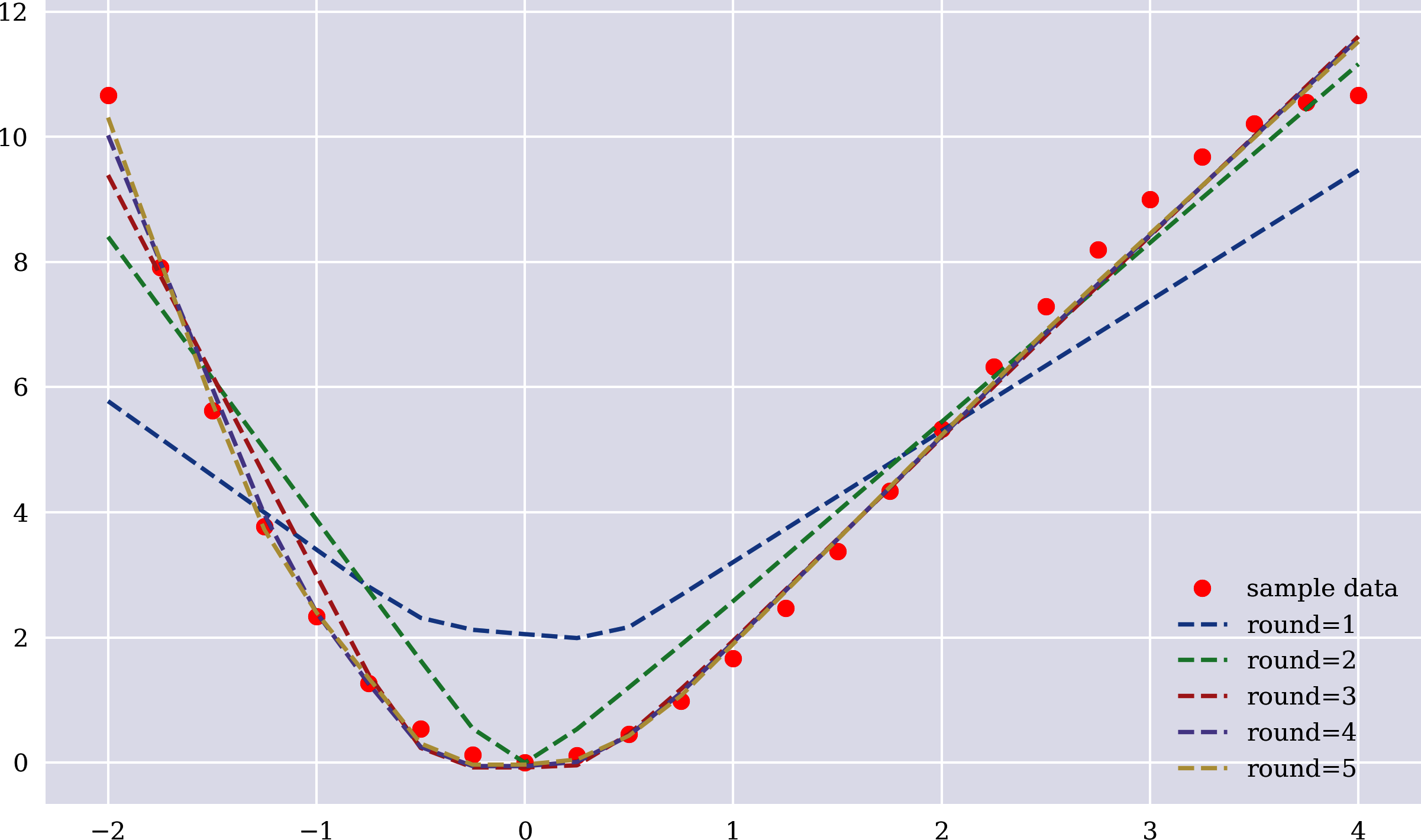
Abbildung 1-6. Beispieldaten und Schätzungen nach mehreren Trainingsrunden

Der folgende Code erzeugt den Zufallsstichproben-Datensatz und erstellt die OLS-Regressionsschätzung auf der Grundlage einer variierenden Anzahl von monomialen Basisfunktionen. Abbildung 1-7 veranschaulicht die Ergebnisse. Selbst für die höchste Anzahl von Monomialfunktionen im Beispiel sind die Schätzergebnisse nicht allzu gut. Der MSE-Wert ist entsprechend relativ hoch:

In [40]: np.random.seed(0)
         x = np.linspace(-1, 1)
         y = np.random.random(len(x)) * 2 - 1

In [41]: plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro', label='sample data')
         for deg in [1, 5, 9, 11, 13, 15]:
             reg = np.polyfit(x, y, deg=deg)
             y_ = np.polyval(reg, x)
             MSE = ((y - y_) ** 2).mean()
             print(f'deg={deg:2d} | MSE={MSE:.5f}')
             plt.plot(x, np.polyval(reg, x), label=f'deg={deg}')
         plt.legend();
         deg= 1 | MSE=0.28153
         deg= 5 | MSE=0.27331
         deg= 9 | MSE=0.25442
         deg=11 | MSE=0.23458
         deg=13 | MSE=0.22989
         deg=15 | MSE=0.21672

Die Ergebnisse für die OLS-Regression sind nicht allzu überraschend. Die OLS-Regression geht in diesem Fall davon aus, dass die Annäherung durch eine geeignete Kombination aus einer endlichen Anzahl von Basisfunktionen erreicht werden kann. Da der Stichprobendatensatz zufällig generiert wurde, schneidet die OLS-Regression in diesem Fall nicht gut ab.

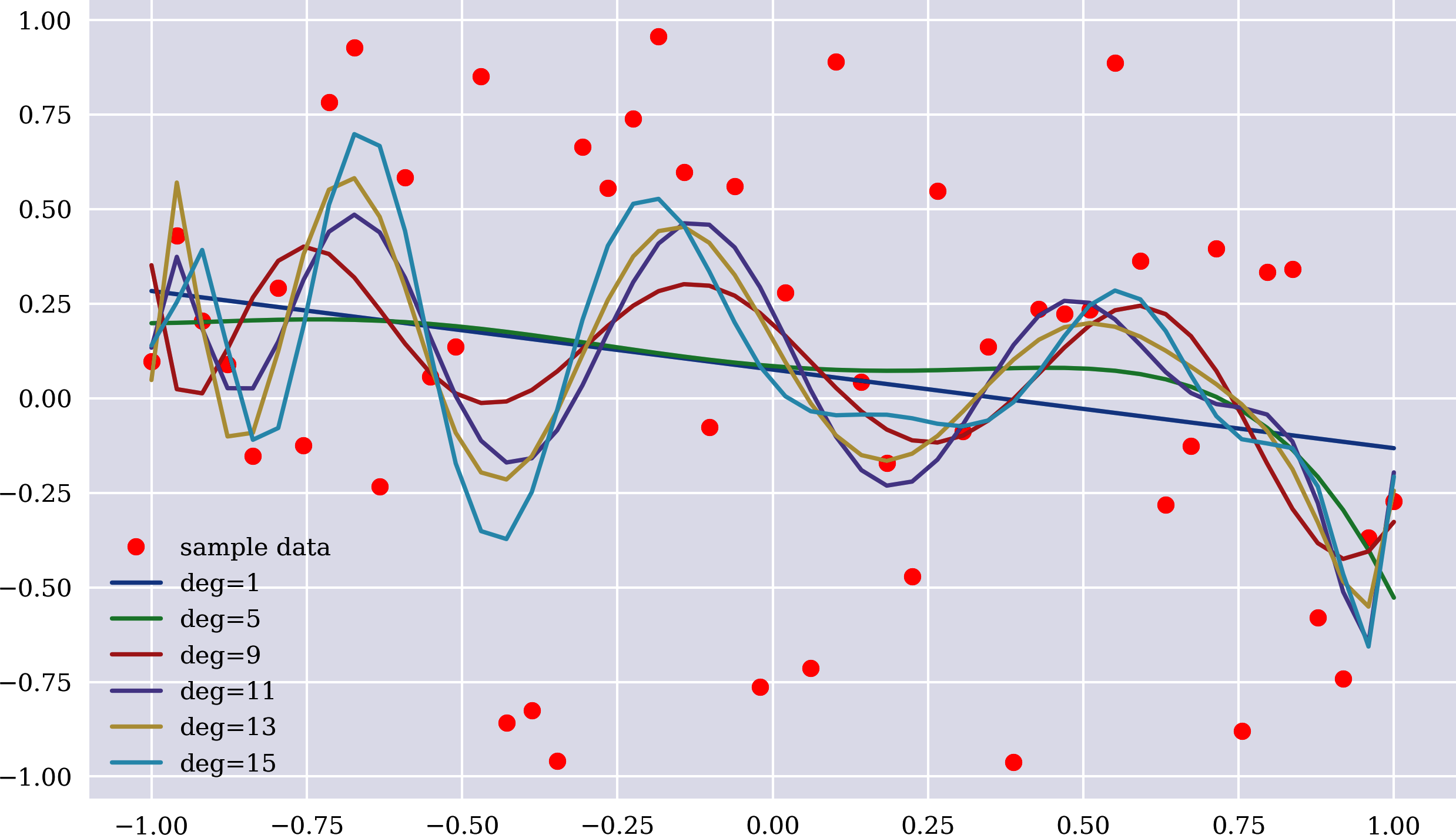
Abbildung 1-7. Daten der Zufallsstichprobe und OLS-Regressionslinien

Was ist mit neuronalen Netzen? Die Anwendung ist genauso einfach wie zuvor und führt zu Schätzungen wie in Abbildung 1-8 dargestellt. Das Endergebnis ist zwar nicht perfekt, aber es ist offensichtlich, dass das neuronale Netz bei der Schätzung der zufälligen Labelwerte aus den zufälligen Merkmalswerten besser abschneidet als die OLS-Regression. Aufgrund seiner Architektur verfügt das neuronale Netz jedoch über fast 200.000 trainierbare Parameter (Gewichte), was eine relativ hohe Flexibilität bietet, insbesondere im Vergleich zur OLS-Regression, bei der maximal 15 + 1 Parameter verwendet werden:

In [42]: model = Sequential()
         model.add(Dense(256, activation='relu', input_dim=1))
         for _ in range(3):
             model.add(Dense(256, activation='relu'))  
         model.add(Dense(1, activation='linear'))
         model.compile(loss='mse', optimizer='rmsprop')

In [43]: model.summary()  
         Model: "sequential_2"
         _________________________________________________________________
         Layer (type)                 Output Shape              Param #
         =================================================================
         dense_3 (Dense)              (None, 256)               512
         _________________________________________________________________
         dense_4 (Dense)              (None, 256)               65792
         _________________________________________________________________
         dense_5 (Dense)              (None, 256)               65792
         _________________________________________________________________
         dense_6 (Dense)              (None, 256)               65792
         _________________________________________________________________
         dense_7 (Dense)              (None, 1)                 257
         =================================================================
         Total params: 198,145
         Trainable params: 198,145
         Non-trainable params: 0
         _________________________________________________________________

In [44]: %%time
         plt.figure(figsize=(10, 6))
         plt.plot(x, y, 'ro', label='sample data')
         for _ in range(1, 8):
             model.fit(x, y, epochs=500, verbose=False)
             y_ =  model.predict(x)
             MSE = ((y - y_.flatten()) ** 2).mean()
             print(f'round={_} | MSE={MSE:.5f}')
             plt.plot(x, y_, '--', label=f'round={_}')
         plt.legend();
         round=1 | MSE=0.13560
         round=2 | MSE=0.08337
         round=3 | MSE=0.06281
         round=4 | MSE=0.04419
         round=5 | MSE=0.03329
         round=6 | MSE=0.07676
         round=7 | MSE=0.00431
         CPU times: user 30.4 s, sys: 4.7 s, total: 35.1 s
         Wall time: 13.6 s

Es werden mehrere versteckte Schichten hinzugefügt.

Die Architektur des Netzwerks und die Anzahl der trainierbaren Parameter werden angezeigt.

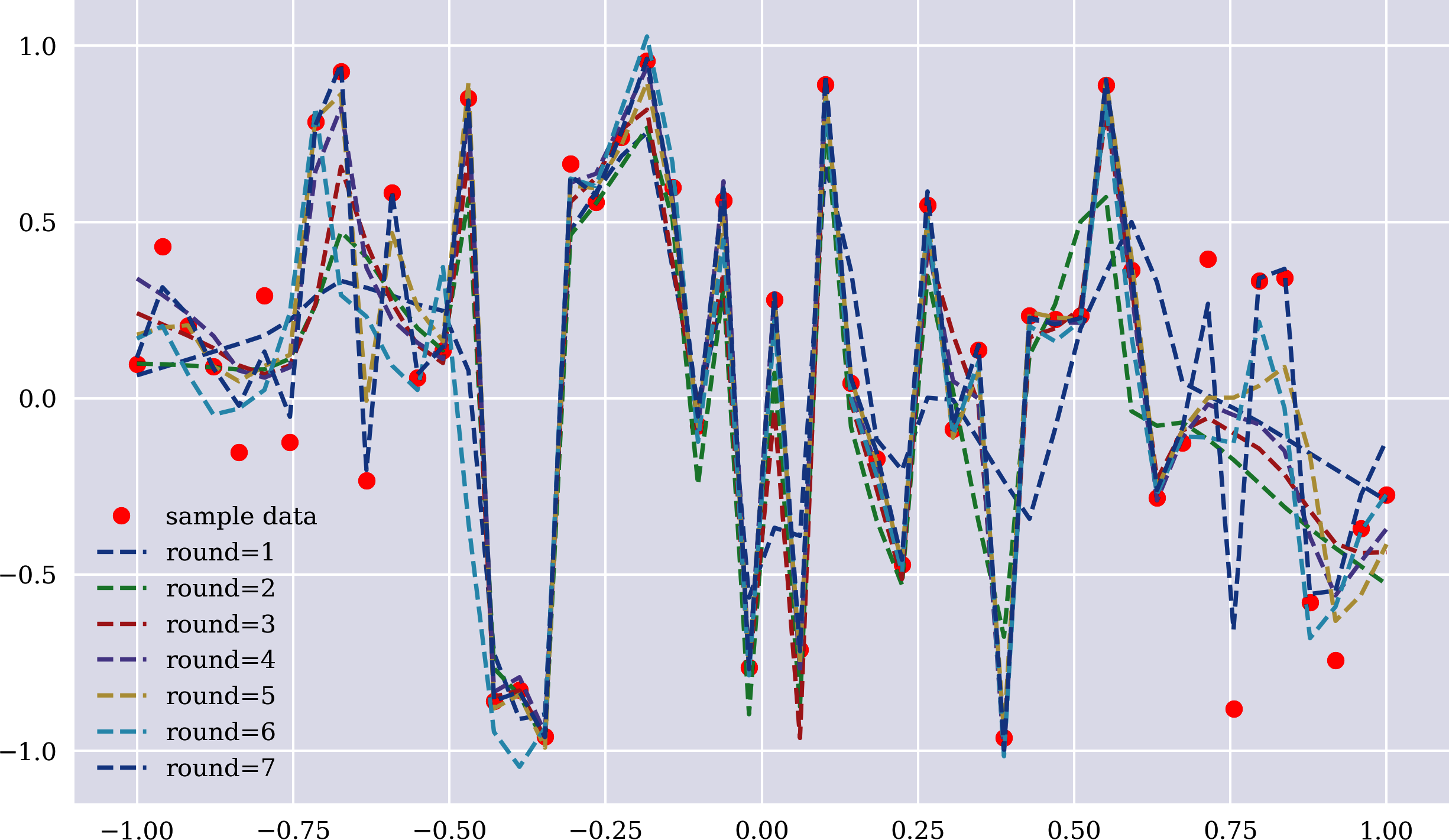
Abbildung 1-8. Zufallsstichprobendaten und Schätzungen des neuronalen Netzes

Klassifizierung mit neuronalen Netzen

Ein weiterer Vorteil von neuronalen Netzen ist, dass sie auch für Klassifizierungsaufgaben verwendet werden können. Betrachte den folgenden Python-Code, der eine Klassifizierung mit einem neuronalen Netz auf der Grundlage von Keras implementiert. Die binären Merkmalsdaten und die Beschriftungsdaten werden nach dem Zufallsprinzip erzeugt. Die wichtigste Anpassung, die bei der Modellierung vorgenommen werden muss, ist die Änderung der Aktivierungsfunktion der Ausgabeschicht von linear auf sigmoid. Weitere Einzelheiten dazu werden in späteren Kapiteln beschrieben. Die Klassifizierung ist nicht perfekt. Sie erreicht jedochein hohes Maß an Genauigkeit. Abbildung 1-9 zeigt, wie sich die Genauigkeit, ausgedrückt als das Verhältnis zwischenrichtigen Ergebnissen und allen Kennzeichnungswerten, mit der Anzahl der Trainingsepochen verändert. Die Genauigkeit fängt niedrig an und verbessert sich dann schrittweise, wenn auch nichtunbedingt mit jedem Schritt:

In [45]: f = 5
         n = 10

In [46]: np.random.seed(100)

In [47]: x = np.random.randint(0, 2, (n, f))  
         x  
Out[47]: array([[0, 0, 1, 1, 1],
                [1, 0, 0, 0, 0],
                [0, 1, 0, 0, 0],
                [0, 1, 0, 0, 1],
                [0, 1, 0, 0, 0],
                [1, 1, 1, 0, 0],
                [1, 0, 0, 1, 1],
                [1, 1, 1, 0, 0],
                [1, 1, 1, 1, 1],
                [1, 1, 1, 0, 1]])

In [48]: y = np.random.randint(0, 2, n)  
         y  
Out[48]: array([1, 1, 0, 0, 1, 1, 0, 1, 0, 1])

In [49]: model = Sequential()
         model.add(Dense(256, activation='relu', input_dim=f))
         model.add(Dense(1, activation='sigmoid'))  
         model.compile(loss='binary_crossentropy', optimizer='rmsprop',
                      metrics=['acc'])  

In [50]: h = model.fit(x, y, epochs=50, verbose=False)
Out[50]: <keras.callbacks.callbacks.History at 0x7fde09dd1cd0>

In [51]: y_ = np.where(model.predict(x).flatten() > 0.5, 1, 0)
         y_
Out[51]: array([1, 1, 0, 0, 0, 1, 0, 1, 0, 1], dtype=int32)




In [52]: y == y_  
Out[52]: array([ True,  True,  True,  True, False,  True,  True,  True,  True,
                 True])

In [53]: res = pd.DataFrame(h.history)  

In [54]: res.plot(figsize=(10, 6));  

Erzeugt zufällige Merkmalsdaten

Erzeugt zufällige Etikettendaten

Definiert die Aktivierungsfunktion für die Ausgabeschicht als sigmoid

Definiert die Verlustfunktion als binary_crossentropy⁶

Vergleicht die vorhergesagten Werte mit den Beschriftungsdaten

Stellt die Verlustfunktion und die Genauigkeitswerte für jeden Trainingsschritt dar

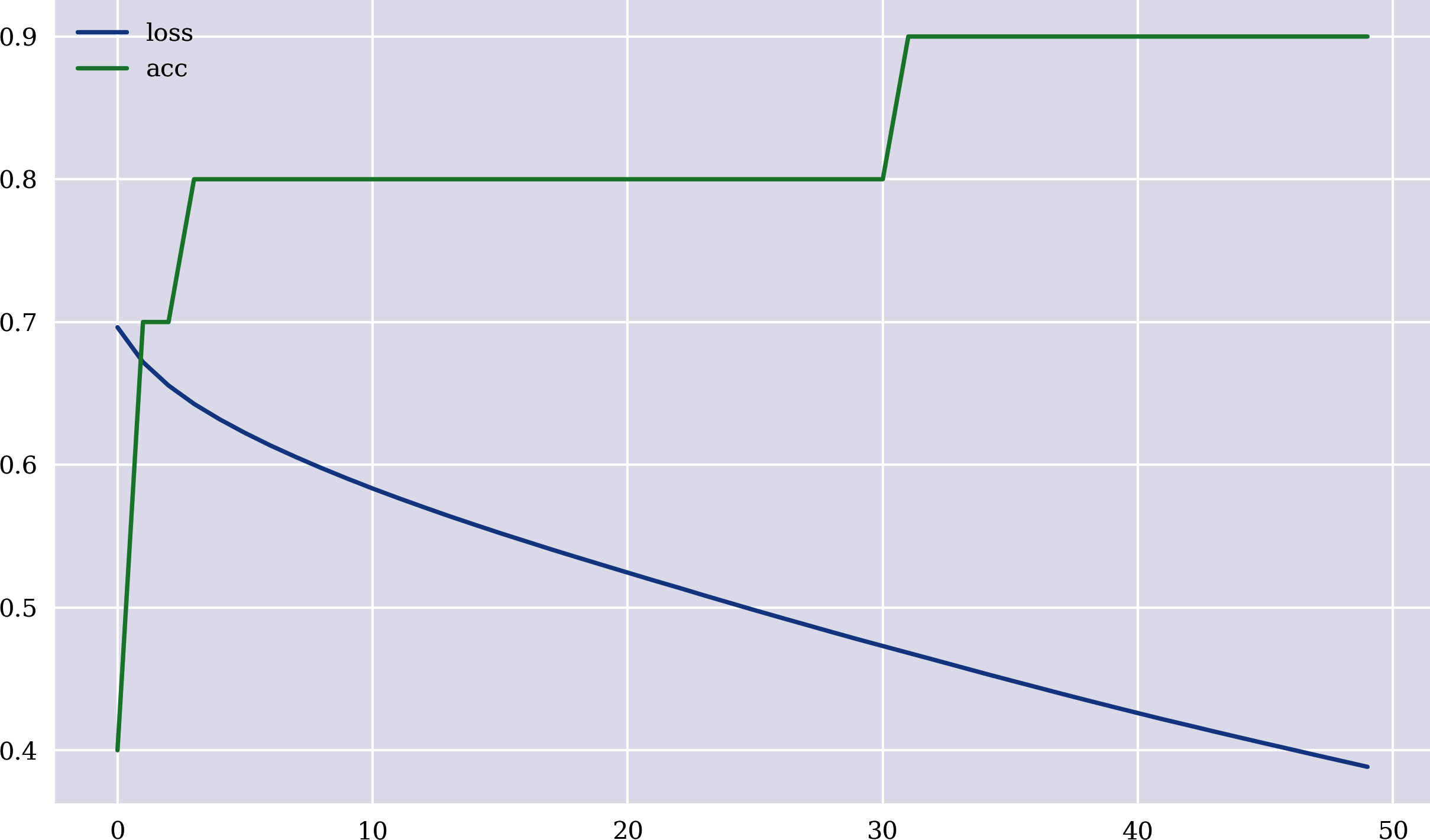
Abbildung 1-9. Klassifizierungsgenauigkeit und Verlust in Abhängigkeit von der Anzahl der Epochen

Die Beispiele in diesem Abschnitt veranschaulichen einige grundlegende Eigenschaften von neuronalen Netzen im Vergleich zur OLS-Regression:

Problemdiagnostisch

Der Ansatz des neuronalen Netzes ist unabhängig, wenn es um die Schätzung und Klassifizierung von Kennzeichnungswerten bei einer Reihe von Merkmalswerten geht. Statistische Methoden, wie die OLS-Regression, können bei einer kleinen Anzahl von Problemen gut funktionieren, bei anderen jedoch nicht so gut oder gar nicht.

Inkrementelles Lernen

Die optimalen Gewichte innerhalb eines neuronalen Netzes werden bei einem angestrebten Erfolgsmaßstab auf der Grundlage einer zufälligen Initialisierung und inkrementeller Verbesserungen schrittweise erlernt. Diese inkrementellen Verbesserungen werden erreicht, indem die Unterschiede zwischen den vorhergesagten Werten und den Werten der Probenkennzeichnung berücksichtigt werden und die Gewichte im neuronalen Netz aktualisiert werden (Backpropagation).

Universelle Angleichung

Es gibt starke mathematische Theoreme, die zeigen, dass neuronale Netze (auch mit nur einer versteckten Schicht) fast jede Funktion annähern können.⁷

Diese Eigenschaften könnten rechtfertigen, warum dieses Buch neuronale Netze in Bezug auf die verwendeten Algorithmen in den Mittelpunkt stellt. In Kapitel 2 werden weitere gute Gründe genannt.

Neuronale Netze

Neuronale Netze sind gut darin, Beziehungen zwischen Eingabe- und Ausgabedaten zu lernen. Sie können für eine Reihe von Problemen eingesetzt werden, z. B. für Schätzungen bei komplexen Zusammenhängen oder für Klassifizierungen, für die herkömmliche statistische Methoden nicht gut geeignet sind.

Die Bedeutung von Daten

Das Beispiel am Ende des vorherigen Abschnitts zeigt, dass neuronale Netze in der Lage sind, Klassifizierungsprobleme recht gut zu lösen. Das neuronale Netz mit einer versteckten Schicht erreicht eine hohe Genauigkeit für den gegebenen Datensatz, oder in-sample. Doch wie steht es um die Vorhersagekraft eines neuronalen Netzes? Diese hängt maßgeblich von der Menge und Vielfalt der Daten ab, die zum Trainieren des neuronalen Netzes zur Verfügung stehen. Ein weiteres Zahlenbeispiel, das auf größeren Datensätzen basiert, soll diesen Punkt verdeutlichen.

Kleiner Datensatz

Betrachte einen Stichproben-Datensatz, der dem zuvor im Klassifizierungsbeispiel verwendeten ähnlich ist, aber mehr Merkmale und mehr Stichproben enthält. Bei den meisten Algorithmen, die in der KI verwendet werden, geht es um Mustererkennung. Im folgenden Python-Code definiert die Anzahl der binären Merkmale die Anzahl der möglichen Muster, über die der Algorithmus etwas lernen kann. Da die Daten der Labels ebenfalls binär sind, versucht der Algorithmus zu lernen, ob ein 0 oder 1 wahrscheinlicher ist, wenn ein bestimmtes Muster vorliegt, z. B. [0, 0, 1, 1, 1, 1, 0, 0, 0, 0]. Da alle Zahlen nach dem Zufallsprinzip mit gleicher Wahrscheinlichkeit ausgewählt werden, gibt es nicht viel zu lernen, abgesehen von der Tatsache, dass die Bezeichnungen 0 und 1 gleich wahrscheinlich sind, egal welches (zufällige) Muster beobachtet wird. Daher sollte ein Basisvorhersagealgorithmus in etwa 50 % der Fälle richtig liegen, unabhängig davon, welches (zufällige) Muster ihmvorgelegt wird:

In [55]: f = 10
         n = 250

In [56]: np.random.seed(100)

In [57]: x = np.random.randint(0, 2, (n, f))  
         x[:4]  
Out[57]: array([[0, 0, 1, 1, 1, 1, 0, 0, 0, 0],
                [0, 1, 0, 0, 0, 0, 1, 0, 0, 1],
                [0, 1, 0, 0, 0, 1, 1, 1, 0, 0],
                [1, 0, 0, 1, 1, 1, 1, 1, 0, 0]])

In [58]: y = np.random.randint(0, 2, n)  
         y[:4]  
Out[58]: array([0, 1, 0, 0])

In [59]: 2 ** f  
Out[59]: 1024

Merkmale Daten

Etiketten Daten

Anzahl der Muster

Um fortzufahren, werden die Rohdaten in ein pandas DataFrame Objekt eingefügt, das bestimmte Operationen und Analysen vereinfacht:

In [60]: fcols = [f'f{_}' for _ in range(f)]  
         fcols  
Out[60]: ['f0', 'f1', 'f2', 'f3', 'f4', 'f5', 'f6', 'f7', 'f8', 'f9']

In [61]: data = pd.DataFrame(x, columns=fcols)  
         data['l'] = y  

In [62]: data.info()  
         <class 'pandas.core.frame.DataFrame'>
         RangeIndex: 250 entries, 0 to 249
         Data columns (total 11 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   f0      250 non-null    int64
          1   f1      250 non-null    int64
          2   f2      250 non-null    int64
          3   f3      250 non-null    int64
          4   f4      250 non-null    int64
          5   f5      250 non-null    int64
          6   f6      250 non-null    int64
          7   f7      250 non-null    int64
          8   f8      250 non-null    int64
          9   f9      250 non-null    int64
          10  l       250 non-null    int64
         dtypes: int64(11)
         memory usage: 21.6 KB

Definiert Spaltennamen für die Merkmalsdaten

Fügt die Merkmalsdaten in ein DataFrame Objekt ein

Fügt die Beschriftungsdaten in das gleiche DataFrame Objekt ein

Zeigt die Metainformationen für den Datensatz an

Anhand der Ergebnisse der Ausführung des folgenden Python-Codes lassen sich zwei große Probleme erkennen. Erstens sind nicht alle Muster im Beispieldatensatz enthalten. Zweitens ist die Stichprobengröße pro beobachtetem Muster viel zu klein. Auch ohne tiefer zu graben, ist klar, dass kein Klassifizierungsalgorithmus wirklich alle möglichen Muster aufsinnvolle Weise kennenlernen kann:

In [63]: grouped = data.groupby(list(data.columns))  

In [64]: freq = grouped['l'].size().unstack(fill_value=0)  

In [65]: freq['sum'] = freq[0] + freq[1]  

In [66]: freq.head(10)  
Out[66]: l                              0  1  sum
         f0 f1 f2 f3 f4 f5 f6 f7 f8 f9
         0  0  0  0  0  0  0  1  1  1   0  1    1
                           1  0  1  0   1  1    2
                                    1   0  1    1
                        1  0  0  0  0   1  0    1
                                    1   0  1    1
                              1  1  1   0  1    1
                           1  0  0  0   0  1    1
                                 1  0   0  1    1
                     1  0  0  0  1  1   1  0    1
                           1  1  0  0   1  0    1

In [67]: freq['sum'].describe().astype(int)  
Out[67]: count    227
         mean       1
         std        0
         min        1
         25%        1
         50%        1
         75%        1
         max        2
         Name: sum, dtype: int64

Gruppiert die Daten entlang aller Spalten

Entstapelt die gruppierten Daten für die Beschriftungsspalte

Addiert die Frequenz für eine 0 und eine 1

Zeigt die Frequenzen für ein 0 und ein 1 für ein bestimmtes Muster

Liefert Statistiken für die Summe der Häufigkeiten

Der folgende Python-Code verwendet das Modell MLPClassifier von scikit-learn.⁸ Das Modell wird mit dem gesamten Datensatz trainiert. Wie sieht es mit der Fähigkeit eines neuronalen Netzwerks aus, über die Beziehungen innerhalb eines bestimmten Datensatzeszu lernen? Die Fähigkeit ist ziemlich hoch, wie die In-Sample-Genauigkeit zeigt. Sie liegt sogar bei fast 100 %, was zu einem großen Teil auf die relativ hohe Kapazität des neuronalen Netzes angesichts des relativ kleinenDatensatzes zurückzuführen ist:

In [68]: from sklearn.neural_network import MLPClassifier
         from sklearn.metrics import accuracy_score

In [69]: model = MLPClassifier(hidden_layer_sizes=[128, 128, 128],
                               max_iter=1000, random_state=100)

In [70]: model.fit(data[fcols], data['l'])
Out[70]: MLPClassifier(hidden_layer_sizes=[128, 128, 128], max_iter=1000,
                       random_state=100)

In [71]: accuracy_score(data['l'], model.predict(data[fcols]))
Out[71]: 0.952

Aber wie sieht es mit der Vorhersagekraft eines trainierten neuronalen Netzes aus? Zu diesem Zweck kann der gegebene Datensatz in einen Trainings- und einen Testdatensatz unterteilt werden. Das Modell wird nur auf dem Trainingsdatensatz trainiert und dann auf seine Vorhersagekraft im Testdatensatz getestet. Wie zuvor ist die Genauigkeit des trainierten neuronalen Netzwerks in der Stichprobe (d. h. auf dem Trainingsdatensatz) ziemlich hoch. Im Testdatensatz ist es jedoch um mehr als 10 Prozentpunkte schlechter als ein uninformierter Basisalgorithmus:

In [72]: split = int(len(data) * 0.7)  

In [73]: train = data[:split]  
         test = data[split:]  

In [74]: model.fit(train[fcols], train['l'])  
Out[74]: MLPClassifier(hidden_layer_sizes=[128, 128, 128], max_iter=1000,
                       random_state=100)

In [75]: accuracy_score(train['l'], model.predict(train[fcols]))  
Out[75]: 0.9714285714285714

In [76]: accuracy_score(test['l'], model.predict(test[fcols]))  
Out[76]: 0.38666666666666666

Teilt die Daten in die Teilmengen train und test auf.

Trainiert das Modell nur auf dem Trainingsdatensatz

Meldet die Genauigkeit in der Stichprobe (Trainingsdatensatz)

Meldet die Genauigkeit außerhalb der Stichprobe (Testdatensatz)

Grob gesagt, lernt das neuronale Netz, das nur auf einem kleinen Datensatz trainiert wurde, aufgrund der beiden identifizierten Hauptprobleme falsche Beziehungen. Die Probleme sind im Zusammenhang mit dem Lernen von Beziehungen in der Stichprobe nicht wirklich relevant. Im Gegenteil: Je kleiner ein Datensatz ist, desto leichter lassen sich Beziehungen in der Stichprobe lernen. Die Problembereiche sind jedoch von großer Bedeutung, wenn das trainierte neuronale Netz zur Erstellung von Vorhersagen außerhalb der Stichprobe verwendet wird.

Größerer Datensatz

Zum Glück gibt es oft einen klaren Ausweg aus dieser problematischen Situation: einen größeren Datensatz. Bei realen Problemen könnte diese theoretische Einsicht ebenso richtig sein. Aus praktischer Sicht sind solche größeren Datensätze jedoch nicht immer verfügbar und lassen sich auch nicht immer so leicht erzeugen. Im Kontext des Beispiels in diesem Abschnitt lässt sich ein größerer Datensatz jedoch tatsächlich leicht erstellen.

Der folgende Python-Code erhöht die Anzahl der Stichproben im anfänglichen Beispieldatensatz erheblich. Das Ergebnis ist, dass die Vorhersagegenauigkeit des trainierten neuronalenNetzes um mehr als 10 Prozentpunkte auf etwa 50 % ansteigt, was angesichts der Beschaffenheit der Etikettendaten zu erwarten ist. Sie entspricht nun der eines uninformierten Basisalgorithmus:

In [77]: factor = 50

In [78]: big = pd.DataFrame(np.random.randint(0, 2, (factor * n, f)),
                            columns=fcols)

In [79]: big['l'] = np.random.randint(0, 2, factor * n)

In [80]: train = big[:split]
         test = big[split:]

In [81]: model.fit(train[fcols], train['l'])
Out[81]: MLPClassifier(hidden_layer_sizes=[128, 128, 128], max_iter=1000,
                       random_state=100)

In [82]: accuracy_score(train['l'], model.predict(train[fcols]))  
Out[82]: 0.9657142857142857

In [83]: accuracy_score(test['l'], model.predict(test[fcols]))  
Out[83]: 0.5043407707910751

Vorhersagegenauigkeit in der Stichprobe (Trainingsdatensatz)

Vorhersagegenauigkeit außerhalb der Stichprobe (Testdatensatz)

Eine schnelle Analyse der verfügbaren Daten, wie sie im Folgenden gezeigt wird, erklärt den Anstieg der Vorhersagegenauigkeit. Erstens sind nun alle möglichen Muster im Datensatz vertreten. Zweitens haben alle Muster eine durchschnittliche Häufigkeit von über 10 im Datensatz. Mit anderen Worten: Das neuronale Netz sieht praktisch alle Muster mehrfach. So kann das neuronale Netz "lernen", dass die Bezeichnungen 0 und 1 für alle möglichen Muster gleich wahrscheinlich sind. Das ist natürlich eine ziemlich umständliche Art, dies zu lernen, aber es ist ein gutes Beispiel dafür, dass ein relativ kleiner Datensatz im Zusammenhang mit neuronalen Netzen oft zu klein sein kann:

In [84]: grouped = big.groupby(list(data.columns))

In [85]: freq = grouped['l'].size().unstack(fill_value=0)

In [86]: freq['sum'] = freq[0] + freq[1]  

In [87]: freq.head(6)
Out[87]: l                               0  1  sum
         f0 f1 f2 f3 f4 f5 f6 f7 f8 f9
         0  0  0  0  0  0  0  0  0  0   10  9   19
                                    1    5  4    9
                                 1  0    2  5    7
                                    1    6  6   12
                              1  0  0    9  8   17
                                    1    7  4   11

In [88]: freq['sum'].describe().astype(int)  
Out[88]: count    1024
         mean       12
         std         3
         min         2
         25%        10
         50%        12
         75%        15
         max        26
         Name: sum, dtype: int64

Fügt die Frequenz für die Werte 0 und 1 hinzu

Zeigt eine zusammenfassende Statistik für die Summenwerte

Volumen und Vielfalt

Bei neuronalen Netzen, die Vorhersageaufgaben erfüllen, sind der Umfang und die Vielfalt der verfügbaren Daten, die zum Training des neuronalen Netzes verwendet werden, entscheidend für seine Vorhersageleistung. Die numerischen, hypothetischen Beispiele in diesem Abschnitt zeigen, dass dasselbe neuronale Netz, das auf einem relativ kleinen und nicht so vielfältigen Datensatz trainiert wurde, um mehr als 10 Prozentpunkte schlechter abschneidet als sein Gegenstück, das auf einem relativ großen und vielfältigen Datensatz trainiert wurde. Dieser Unterschied kann als gewaltig angesehen werden, wenn man bedenkt, dass KI-Praktiker und Unternehmen oft um Verbesserungen kämpfen, die nur einen Zehntelprozentpunkt ausmachen.

Big Data

Was ist der Unterschied zwischen einem größeren Datensatz und einem großen Datensatz? Der Begriff "Big Data" wird seit mehr als einem Jahrzehnt für eine Reihe von Dingen verwendet. Für die Zwecke dieses Buches könnte man sagen, dass ein großer Datensatz groß genug ist - in Bezug auf Volumen, Vielfalt und vielleicht auch Geschwindigkeit -, um einen KI-Algorithmus so zu trainieren, dass er bei einer Vorhersageaufgabe besser abschneidet als ein Basisalgorithmus.

Der zuvor verwendete größere Datensatz ist in der Praxis immer noch klein. Er ist jedoch groß genug, um das vorgegebene Ziel zu erreichen. Der erforderliche Umfang und die Vielfalt des Datensatzes hängen vor allem von der Struktur und den Merkmalen der Merkmals- und Kennzeichnungsdaten ab.

Nehmen wir an, dass eine Privatkundenbank einen auf einem neuronalen Netzwerk basierenden Klassifizierungsansatz für die Kreditwürdigkeitsprüfung einführt. Ausgehend von den internen Daten entwickelt der zuständige Datenwissenschaftler 25 kategoriale Merkmale, von denen jedes 8 verschiedene Werte annehmen kann. Die daraus resultierende Anzahl von Mustern ist astronomisch groß:

In [89]: 8 ** 25
Out[89]: 37778931862957161709568

Es ist klar, dass kein einziger Datensatz ein neuronales Netz mit jedem einzelnen dieser Muster vertraut machen kann.⁹ Glücklicherweise ist dies in der Praxis nicht notwendig, damit das neuronale Netz anhand von Daten über reguläre, säumige und/oder abgelehnte Schuldner etwas über die Kreditwürdigkeit lernen kann. Es ist auch nicht notwendig, generell "gute" Vorhersagen über die Kreditwürdigkeit jedes potenziellen Schuldners zu treffen.

Dafür gibt es eine Reihe von Gründen. Um nur einige zu nennen: Erstens wird nicht jedes Muster in der Praxis relevant sein - manche Muster gibt es vielleicht gar nicht, sind unmöglich usw. Zweitens sind vielleicht nicht alle Merkmale gleich wichtig, was die Anzahl der relevanten Merkmale und damit die Anzahl der möglichen Muster reduziert. Drittens kann es sein, dass ein Wert von 4 oder 5 für die Merkmalsnummer 7 überhaupt keinen Unterschied macht, was die Zahl der relevanten Muster weiter reduziert.

Schlussfolgerungen

In diesem Buch umfasst Künstliche Intelligenz (KI) Methoden, Techniken, Algorithmen und so weiter, die in der Lage sind, Beziehungen, Regeln, Wahrscheinlichkeiten und mehr aus Daten zu lernen. Der Schwerpunkt liegt auf überwachten Lernalgorithmen, z. B. für Schätzungen und Klassifizierungen. Bei den Algorithmen stehen neuronale Netze und Deep Learning-Ansätze im Mittelpunkt.

Das zentrale Thema dieses Buches ist die Anwendung neuronaler Netze auf eines der Kernprobleme im Finanzwesen: die Vorhersage zukünftiger Marktbewegungen. Genauer gesagt geht es um die Vorhersage der Bewegungsrichtung eines Aktienindexes oder des Wechselkurses eines Währungspaares. Die Vorhersage der zukünftigen Marktrichtung (d. h. ob ein Zielwert oder ein Preis nach oben oder unten geht) ist ein Problem, das sich leicht in eine Klassifizierungsumgebung übertragen lässt.

Bevor wir tiefer in das eigentliche Thema eintauchen, werden im nächsten Kapitel zunächst ausgewählte Themen im Zusammenhang mit der sogenannten Superintelligenz und der technologischen Singularität erörtert. Diese Diskussion liefert nützliche Hintergrundinformationen für die folgenden Kapitel, die sich mit Finanzen und der Anwendung von KI im Finanzbereich beschäftigen.

Referenzen

In diesem Kapitel zitierte Bücher und Artikel:

• Alpaydin, Ethem. 2016. Maschinelles Lernen. MIT Press, Cambridge.

• Chollet, Francois. 2017. Deep Learning mit Python. Shelter Island: Manning.

• Goodfellow, Ian, Yoshua Bengio, und Aaron Courville. 2016. Deep Learning. Cambridge: MIT Press. http://deeplearningbook.org.

• Kratsios, Anastasis. 2019. "Universal Approximation Theorems. " https://oreil.ly/COOdI.

• Silver, David et al. 2016. "Das Go-Spiel mit tiefen neuronalen Netzen und Baumsuche meistern". Nature 529 (Januar): 484-489.

• Shanahan, Murray. 2015. Die technologische Singularität. Cambridge: MIT Press.

• Tegmark, Max. 2017. Leben 3.0: Menschsein im Zeitalter der künstlichen Intelligenz. Vereinigtes Königreich: Penguin Random House.

• VanderPlas, Jake. 2017. Python Data Science Handbook. Sebastopol: O'Reilly.

¹ Für Details siehe sklearn.cluster.KMeans und VanderPlas (2017, Kap. 5).

² Für Details siehe VanderPlas (2017, Kap. 5).

³ Für Details, siehe sklearn.neural_network.MLPRegressor. Für weitere Hintergrundinformationen siehe Goodfellow et al. (2016, Kap. 6).

⁴ Für Details siehe Chollet (2017, Kap. 3).

⁵ Einzelheiten zu Aktivierungsfunktionen mit Keras findest du unter https://keras.io/activations.

⁶ Die Verlustfunktion berechnet den Vorhersagefehler des neuronalen Netzes (oder anderer ML-Algorithmen). Die binäre Kreuzentropie ist eine geeignete Verlustfunktion für binäre Klassifizierungsprobleme, während der mittlere quadratische Fehler (MSE) z. B. für Schätzungsprobleme geeignet ist. Einzelheiten zu Verlustfunktionen mit Keras findest du unter https://keras.io/losses.

⁷ Siehe z. B. Kratsios (2019).

⁸ Für Details, siehe sklearn.neural_network.MLPClassifier.

⁹ Auch wäre es mit der heutigen Rechentechnik nicht möglich, ein neuronales Netz auf der Grundlage eines solchen Datensatzes zu modellieren und zu trainieren, wenn es verfügbar wäre. In diesem Zusammenhang befasst sich das nächste Kapitel mit der Bedeutung von Hardware für KI.