22 Jeffrey-Hamel Flow

The Jeffrey-Hamel flow refers to a two-dimensional flow in the region between two intersecting plane walls. The steady flow between the stationary walls is caused by the presence of a source or sink of fluid at the point of intersection of the walls. This example affords an impressive illustration of the combined effects of convection and diffusion of vorticity generated at a rigid boundary. In addition, it plays a role in the development of viscous flow theory similar to that played by the two-dimensional Ising (1925) model in developing the theory of critical phenomena (Stanley, 1971).

22.1 The Exact Solution

Let us use the cylindrical polar coordinates left-parenthesis r comma theta right-parenthesis with the plane walls located at theta equals plus alpha (Figure 22.1). The equations governing this flow are

(1) rho left-parenthesis u Subscript r Baseline StartFraction partial-differential u Subscript r Baseline Over partial-differential r EndFraction plus u Subscript theta Baseline StartFraction partial-differential u Subscript r Baseline Over r partial-differential theta EndFraction minus StartFraction u Subscript theta Superscript 2 Baseline Over r EndFraction right-parenthesis equals minus StartFraction partial-differential p Over partial-differential r EndFraction plus mu left-parenthesis nabla squared u Subscript r Baseline minus StartFraction u Subscript r Baseline Over r squared EndFraction minus 2 StartFraction partial-differential u Subscript theta Baseline Over r squared partial-differential theta EndFraction right-parenthesis
(2) rho left-parenthesis u Subscript r Baseline StartFraction partial-differential u Subscript theta Baseline Over partial-differential r EndFraction plus u Subscript theta Baseline StartFraction partial-differential u Subscript theta Baseline Over r partial-differential theta EndFraction plus StartFraction u Subscript r Baseline u Subscript theta Baseline Over r EndFraction right-parenthesis equals minus StartFraction partial-differential p Over r partial-differential theta EndFraction plus mu left-parenthesis nabla squared u Subscript theta Baseline minus StartFraction u Subscript theta Baseline Over r squared EndFraction plus 2 StartFraction partial-differential u Subscript r Baseline Over r squared partial-differential theta EndFraction right-parenthesis
(3) StartFraction partial-differential u Subscript r Baseline Over partial-differential r EndFraction plus StartFraction u Subscript r Baseline Over r EndFraction plus StartFraction 1 Over r EndFraction StartFraction partial-differential u Subscript theta Baseline Over partial-differential theta EndFraction equals 0

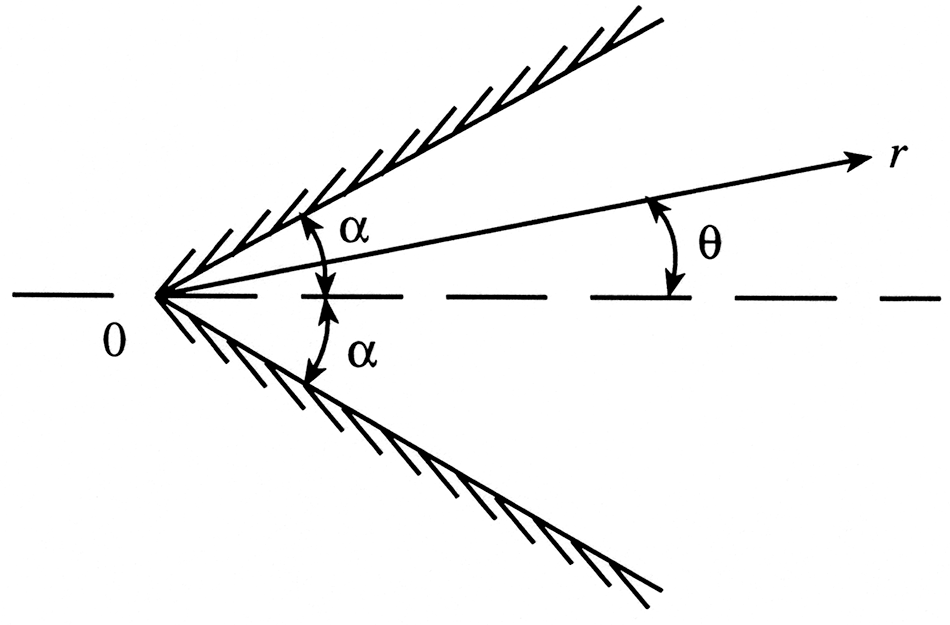
Figure 22.1 The Jeffrey-Hamel flow.

where

Let us consider a purely radial flow, and look for solutions ...

Get Introduction to Theoretical and Mathematical Fluid Dynamics now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial