Chapter 9
Linear Stochastic Differential Equations
9.1. Explicit solution of a linear SDE
DEFINITION 9.1.– A linear stochastic differential equation (LSDE) is an equation of the form
[9.1]![]()
where ai and bi (i = 1, 2) are non-random functions bounded on every finite interval [0, T](e.g. continuous); it is easy to check that the coefficients of an LSDE satisfy the Lipschitz conditions, and thus the equation has a unique solution. If ai and bi are constants, then the LSDE is called autonomous; if a2 = b2 = 0, then it is called homogeneous.
Denote
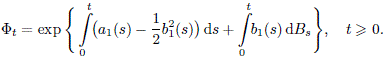
PROPOSITION 9.2.– The random process Φt, t ![]() 0, is a solution of the homogeneous LSDE
0, is a solution of the homogeneous LSDE
[9.2]![]()
with the initial condition Y0 = 1. The process Φ is called the fundamental solution of equation [9.2]
Proof. Denote
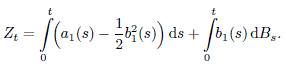
Thus, Φt = eZt, t ![]() 0. Then, using Itô's formula, we get:
0. Then, using Itô's formula, we get:
The initial condition Φ0 = 1 is clearly satisfied.
PROPOSITION 9.3.– The ...
Get Introduction to Stochastic Analysis: Integrals and Differential Equations now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

