Introduction to Probability and Stochastic Processes with Applications

APPENDIX C

TOPICS ON LINEAR ALGEBRA

This appendix presents some of the results from linear algebra used throughout the book. It is assumed that the reader has some knowledge of basic matrix theory. The reader interested in further reading on this topics is referred to Searle (1982).

1. The vectors in ⁿ are considered to be row-vectors. If x = (x₁, … , x_n) and y = (y₁, … , y_n) are vectors in ⁿ, then their inner product is defined as:

   

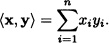
   The Euclidean norm of a vector x = (x₁, … , x_n) of ⁿ is the real number

2. The determinant of a square matrix A is notated det (A).
3. The trace of a square matrix A is written tr (A).
4. The transpose of a matrix A is notated A^T.
5. A square matrix is said to be diagonal if all the off-diagonal elements are equal to zero.
6. A diagonal matrix having only 1’s in its main diagonal is called the identity of order n (n being the size of the matrix) and is written as I_n.
7. A square matrix A is said to be symmetric if it is equal to its transpose.
8. A square matrix of order n is said ...