Chapter 4. Pathfinding and Graph Search Algorithms
Graph search algorithms explore a graph either for general discovery or explicit search. These algorithms carve paths through the graph, but there is no expectation that those paths are computationally optimal. We will cover Breadth First Search and Depth First Search because they are fundamental for traversing a graph and are often a required first step for many other types of analysis.
Pathfinding algorithms build on top of graph search algorithms and explore routes between nodes, starting at one node and traversing through relationships until the destination has been reached. These algorithms are used to identify optimal routes through a graph for uses such as logistics planning, least cost call or IP routing, and gaming simulation.
Specifically, the pathfinding algorithms we’ll cover are:
- Shortest Path, with two useful variations (A* and Yen’s)
-
Finding the shortest path or paths between two chosen nodes
- All Pairs Shortest Path and Single Source Shortest Path
-
For finding the shortest paths between all pairs or from a chosen node to all others
- Minimum Spanning Tree
-
For finding a connected tree structure with the smallest cost for visiting all nodes from a chosen node
- Random Walk
-
Because it’s a useful preprocessing/sampling step for machine learning workflows and other graph algorithms
In this chapter we’ll explain how these algorithms work and show examples in Spark and Neo4j. In cases where an algorithm is only available in one platform, we’ll provide just that one example or illustrate how you can customize our implementation.
Figure 4-1 shows the key differences between these types of algorithms, and Table 4-1 is a quick reference to what each algorithm computes with an example use.
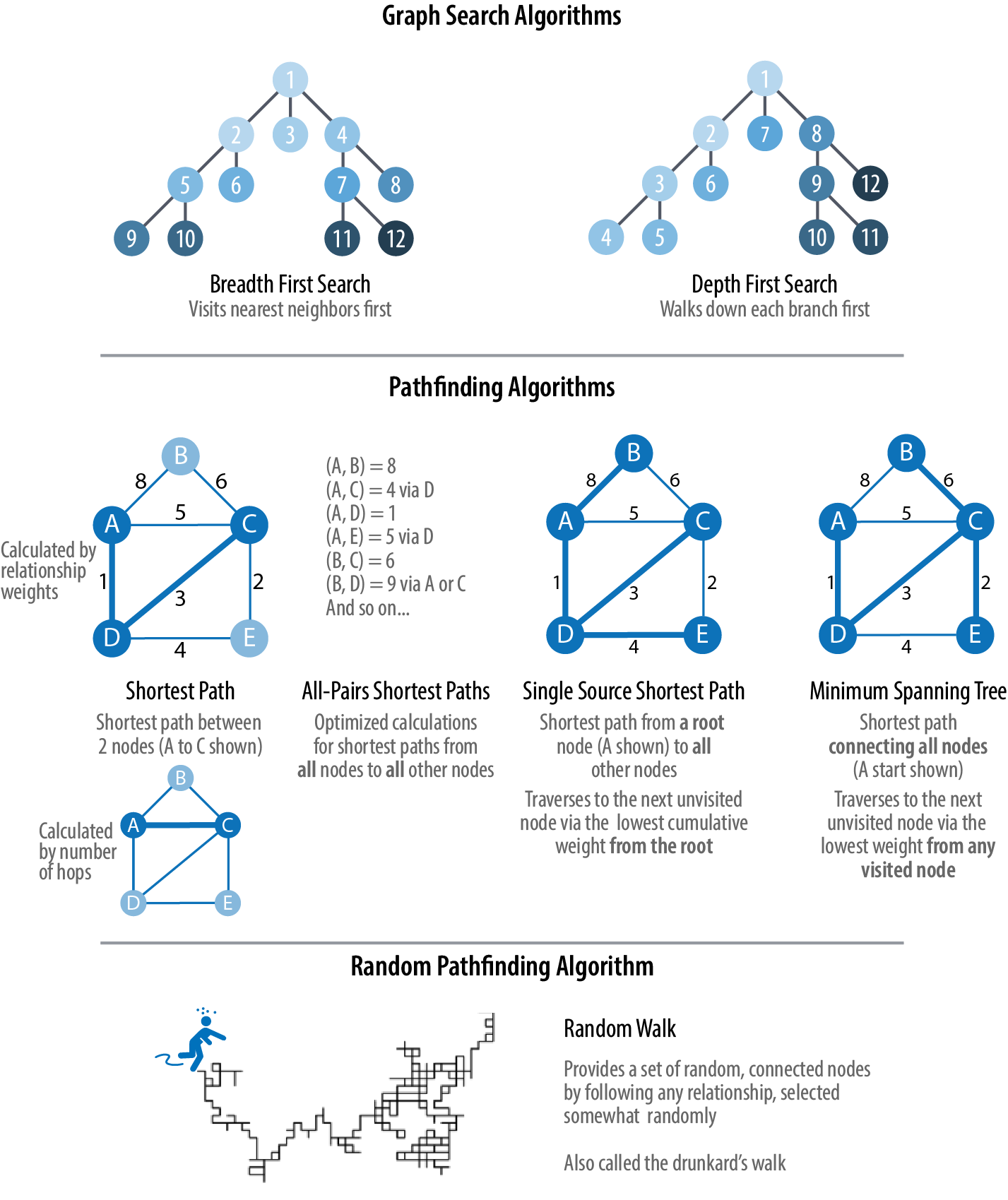
Figure 4-1. Pathfinding and search algorithms
| Algorithm type | What it does | Example use | Spark example | Neo4j example |
|---|---|---|---|---|
Traverses a tree structure by fanning out to explore the nearest neighbors and then their sublevel neighbors |
Locating neighbor nodes in GPS systems to identify nearby places of interest |
Yes |
No |
|
Traverses a tree structure by exploring as far as possible down each branch before backtracking |
Discovering an optimal solution path in gaming simulations with hierarchical choices |
No |
No |
|
Calculates the shortest path between a pair of nodes |
Finding driving directions between two locations |
Yes |
Yes |
|
Calculates the shortest path between all pairs of nodes in the graph |
Evaluating alternate routes around a traffic jam |
Yes |
Yes |
|
Calculates the shorest path between a single root node and all other nodes |
Least cost routing of phone calls |
Yes |
Yes |
|
Calculates the path in a connected tree structure with the smallest cost for visiting all nodes |
Optimizing connected routing, such as laying cable or garbage collection |
No |
Yes |
|
Returns a list of nodes along a path of specified size by randomly choosing relationships to traverse. |
Augmenting training for machine learning or data for graph algorithms. |
No |
Yes |
First we’ll take a look at the dataset for our examples and walk through how to import the data into Apache Spark and Neo4j. For each algorithm, we’ll start with a short description of the algorithm and any pertinent information on how it operates. Most sections also include guidance on when to use related algorithms. Finally, we provide working sample code using the sample dataset at the end of each algorithm section.
Let’s get started!
Example Data: The Transport Graph
All connected data contains paths between nodes, which is why search and pathfinding are the starting points for graph analytics. Transportation datasets illustrate these relationships in an intuitive and accessible way. The examples in this chapter run against a graph containing a subset of the European road network. You can download the nodes and relationships files from the book’s GitHub repository.
| id | latitude | longitude | population |
|---|---|---|---|
Amsterdam |
52.379189 |
4.899431 |
821752 |
Utrecht |
52.092876 |
5.104480 |
334176 |
Den Haag |
52.078663 |
4.288788 |
514861 |
Immingham |
53.61239 |
-0.22219 |
9642 |
Doncaster |
53.52285 |
-1.13116 |
302400 |
Hoek van Holland |
51.9775 |
4.13333 |
9382 |
Felixstowe |
51.96375 |
1.3511 |
23689 |
Ipswich |
52.05917 |
1.15545 |
133384 |
Colchester |
51.88921 |
0.90421 |
104390 |
London |
51.509865 |
-0.118092 |
8787892 |
Rotterdam |
51.9225 |
4.47917 |
623652 |
Gouda |
52.01667 |
4.70833 |
70939 |
| src | dst | relationship | cost |
|---|---|---|---|
Amsterdam |
Utrecht |
EROAD |
46 |
Amsterdam |
Den Haag |
EROAD |
59 |
Den Haag |
Rotterdam |
EROAD |
26 |
Amsterdam |
Immingham |
EROAD |
369 |
Immingham |
Doncaster |
EROAD |
74 |
Doncaster |
London |
EROAD |
277 |
Hoek van Holland |
Den Haag |
EROAD |
27 |
Felixstowe |
Hoek van Holland |
EROAD |
207 |
Ipswich |
Felixstowe |
EROAD |
22 |
Colchester |
Ipswich |
EROAD |
32 |
London |
Colchester |
EROAD |
106 |
Gouda |
Rotterdam |
EROAD |
25 |
Gouda |
Utrecht |
EROAD |
35 |
Den Haag |
Gouda |
EROAD |
32 |
Hoek van Holland |
Rotterdam |
EROAD |
33 |
Figure 4-2 shows the target graph that we want to construct.

Figure 4-2. The transport graph
For simplicity we consider the graph in Figure 4-2 to be undirected because most roads between cities are bidirectional. We’d get slightly different results if we evaluated the graph as directed because of the small number of one-way streets, but the overall approach remains similar. However, both Spark and Neo4j operate on directed graphs. In cases like this where we want to work with undirected graphs (e.g., bidirectional roads), there is an easy way to accomplish that:
-
For Spark, we’ll create two relationships for each row in transport-relationships.csv—one going from
dsttosrcand one fromsrctodst. -
For Neo4j, we’ll create a single relationship and then ignore the relationship direction when we run the algorithms.
Having understood those little modeling workarounds, we can now get on with loading graphs into Spark and Neo4j from the example CSV files.
Importing the Data into Apache Spark
Starting with Spark, we’ll first import the packages we need from Spark and the GraphFrames package:
frompyspark.sql.typesimport*fromgraphframesimport*
The following function creates a GraphFrame from the example CSV files:
defcreate_transport_graph():node_fields=[StructField("id",StringType(),True),StructField("latitude",FloatType(),True),StructField("longitude",FloatType(),True),StructField("population",IntegerType(),True)]nodes=spark.read.csv("data/transport-nodes.csv",header=True,schema=StructType(node_fields))rels=spark.read.csv("data/transport-relationships.csv",header=True)reversed_rels=(rels.withColumn("newSrc",rels.dst).withColumn("newDst",rels.src).drop("dst","src").withColumnRenamed("newSrc","src").withColumnRenamed("newDst","dst").select("src","dst","relationship","cost"))relationships=rels.union(reversed_rels)returnGraphFrame(nodes,relationships)
Loading the nodes is easy, but for the relationships we need to do a little preprocessing so that we can create each relationship twice.
Now let’s call that function:
g=create_transport_graph()
Importing the Data into Neo4j
Now for Neo4j. We’ll start by creating a database that we’ll use for the examples in this chapter:
:usesystem;CREATEDATABASEchapter4;:usechapter4;

Switch to the system database.

Create a new database with the name
chapter4. This operation is asynchronous so we may have to wait a couple of seconds before switching to the database.
Switch to the
chapter4database.
Now let’s load the nodes:
WITH'https://github.com/neo4j-graph-analytics/book/raw/master/data/'ASbaseWITHbase +'transport-nodes.csv'ASuriLOAD CSVWITHHEADERS FROM uriASrowMERGE (place:Place {id:row.id})SETplace.latitude = toFloat(row.latitude),place.longitude = toFloat(row.longitude),place.population = toInteger(row.population);
And now the relationships:
WITH'https://github.com/neo4j-graph-analytics/book/raw/master/data/'ASbaseWITHbase +'transport-relationships.csv'ASuriLOAD CSVWITHHEADERS FROM uriASrowMATCH(origin:Place {id: row.src})MATCH(destination:Place {id: row.dst})MERGE (origin)-[:EROAD {distance: toInteger(row.cost)}]->(destination);
Although we’re storing directed relationships, we’ll ignore the direction when we execute algorithms later in the chapter.
Breadth First Search
Breadth First Search (BFS) is one of the fundamental graph traversal algorithms. It starts from a chosen node and explores all of its neighbors at one hop away before visiting all the neighbors at two hops away, and so on.
The algorithm was first published in 1959 by Edward F. Moore, who used it to find the shortest path out of a maze. It was then developed into a wire routing algorithm by C. Y. Lee in 1961, as described in “An Algorithm for Path Connections and Its Applications”.
BFS is most commonly used as the basis for other more goal-oriented algorithms. For example, Shortest Path, Connected Components, and Closeness Centrality all use the BFS algorithm. It can also be used to find the shortest path between nodes.
Figure 4-3 shows the order in which we would visit the nodes of our transport graph if we were performing a breadth first search that started from the Dutch city, Den Haag (in English, The Hague). The numbers next to the city name indicate the order in which each node is visited.

Figure 4-3. Breadth First Search starting from Den Haag. Node numbers indicate the order traversed.
We first visit all of Den Haag’s direct neighbors, before visiting their neighbors, and their neighbors’ neighbors, until we’ve run out of relationships to traverse.
Breadth First Search with Apache Spark
Spark’s implementation of the Breadth First Search algorithm finds the shortest path between two nodes by the number of relationships (i.e., hops) between them. You can explicitly name your target node or add criteria to be met.
For example, we can use the bfs function to find the first medium-sized (by European standards) city that has a population of between 100,000 and 300,000 people.
Let’s first check which places have a population matching those criteria:
(g.vertices.filter("population > 100000 and population < 300000").sort("population").show())
This is the output we’ll see:
| id | latitude | longitude | population |
|---|---|---|---|
Colchester |
51.88921 |
0.90421 |
104390 |
Ipswich |
52.05917 |
1.15545 |
133384 |
There are only two places matching our criteria, and we’d expect to reach Ipswich first based on a breadth first search.
The following code finds the shortest path from Den Haag to a medium-sized city:
from_expr="id='Den Haag'"to_expr="population > 100000 and population < 300000 and id <> 'Den Haag'"result=g.bfs(from_expr,to_expr)
result contains columns that describe the nodes and relationships between the two cities.
We can run the following code to see the list of columns returned:
(result.columns)
This is the output we’ll see:
['from', 'e0', 'v1', 'e1', 'v2', 'e2', 'to']
Columns beginning with e represent relationships (edges) and columns beginning with v represent nodes (vertices).
We’re only interested in the nodes, so let’s filter out any columns that begin with e from the resulting DataFrame:
columns=[columnforcolumninresult.columnsifnotcolumn.startswith("e")]result.select(columns).show()
If we run the code in pyspark we’ll see this output:
| from | v1 | v2 | to |
|---|---|---|---|
[Den Haag, 52.078… |
[Hoek van Holland… |
[Felixstowe, 51.9… |
[Ipswich, 52.0591… |
As expected, the bfs algorithm returns Ipswich!
Remember that this function is satisfied when it finds the first match, and as you can see in Figure 4-3, Ipswich is evaluated before Colchester.
Depth First Search
Depth First Search (DFS) is the other fundamental graph traversal algorithm. It starts from a chosen node, picks one of its neighbors, and then traverses as far as it can along that path before backtracking.
DFS was originally invented by French mathematician Charles Pierre Trémaux as a strategy for solving mazes. It provides a useful tool to simulate possible paths for scenario modeling. Figure 4-4 shows the order in which we would visit the nodes of our transport graph if we were performing a DFS that started from Den Haag.

Figure 4-4. Depth First Search starting from Den Haag. Node numbers indicate the order traversed.
Notice how different the node order is compared to BFS. For this DFS, we start by traversing from Den Haag to Amsterdam, and are then able to get to every other node in the graph without needing to backtrack at all!
We can see how search algorithms lay the groundwork for moving through graphs. Now let’s look at the pathfinding algorithms that find the cheapest path in terms of the number of hops or weight. Weights can be anything measured, such as time, distance, capacity, or cost.
Shortest Path
The Shortest Path algorithm calculates the shortest (weighted) path between a pair of nodes. It’s useful for user interactions and dynamic workflows because it works in real time.
Pathfinding has a history dating back to the 19th century and is considered to be a classic graph problem. It gained prominence in the early 1950s in the context of alternate routing; that is, finding the second-shortest route if the shortest route is blocked. In 1956, Edsger Dijkstra created the best-known of these algorithms.
Dijkstra’s Shortest Path algorithm operates by first finding the lowest-weight relationship from the start node to directly connected nodes. It keeps track of those weights and moves to the “closest” node. It then performs the same calculation, but now as a cumulative total from the start node. The algorithm continues to do this, evaluating a “wave” of cumulative weights and always choosing the lowest weighted cumulative path to advance along, until it reaches the destination node.
Note
You’ll notice in graph analytics the use of the terms weight, cost, distance, and hop when describing relationships and paths. “Weight” is the numeric value of a particular property of a relationship. “Cost” is used similarly, but we’ll see it more often when considering the total weight of a path.
“Distance” is often used within an algorithm as the name of the relationship property that indicates the cost of traversing between a pair of nodes. It’s not required that this be an actual physical measure of distance. “Hop” is commonly used to express the number of relationships between two nodes. You may see some of these terms combined, as in “It’s a five-hop distance to London” or “That’s the lowest cost for the distance.”
When Should I Use Shortest Path?
Use Shortest Path to find optimal routes between a pair of nodes, based on either the number of hops or any weighted relationship value. For example, it can provide real-time answers about degrees of separation, the shortest distance between points, or the least expensive route. You can also use this algorithm to simply explore the connections between particular nodes.
Example use cases include:
-
Finding directions between locations. Web-mapping tools such as Google Maps use the Shortest Path algorithm, or a close variant, to provide driving directions.
-
Finding the degrees of separation between people in social networks. For example, when you view someone’s profile on LinkedIn, it will indicate how many people separate you in the graph, as well as listing your mutual connections.
-
Finding the number of degrees of separation between an actor and Kevin Bacon based on the movies they’ve appeared in (the Bacon Number). An example of this can be seen on the Oracle of Bacon website. The Erdös Number Project provides a similar graph analysis based on collaboration with Paul Erdös, one of the most prolific mathematicians of the twentieth century.
Shortest Path with Neo4j
The Neo4j Graph Data Science library has a built-in procedure that we can use to compute both unweighted and weighted shortest paths. Let’s first learn how to compute unweighted shortest paths.
Neo4j’s Shortest Path algorithm takes in a config map with the following keys:
startNode-
The node where our shortest path search begins.
endNode-
The node where our shortest path search ends.
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
relationshipWeightProperty-
The relationship property that indicates the cost of traversing between a pair of nodes. The cost is the number of kilometers between two locations.
To have Neo4j’s Shortest Path algorithm ignore weights we won’t set the relationshipWeightProperty key.
The algorithm will then assume a default weight of 1.0 for each relationship.
The following query computes the unweighted shortest path from Amsterdam to London:
MATCH(source:Place {id:"Amsterdam"}),(destination:Place {id:"London"})CALL gds.alpha.shortestPath.stream({startNode: source,endNode: destination,nodeProjection:"*",relationshipProjection: {all: {type:"*",orientation:"UNDIRECTED"}}})YIELD nodeId, costRETURNgds.util.asNode(nodeId).idASplace, cost;
In this query we are passing nodeProjection: "*", which means that all node labels should be considered.
The relationshipProjection is a bit more complicated.
We’re using the advanced configuration mode, which enables a more flexible definition of the relationship types to consider during the traversal.
Let’s break down the values that we passed in:
type: "*"-
All relationship types should be considered.
orientation: "UNDIRECTED"-
Each relationship in the underlying graph is projected in both directions.
Note
More detailed documentation about node and relationship projections can be found in the Native Projection chapter of the Graph Data Science user manual.
This query returns the following output:
| place | cost |
|---|---|
Amsterdam |
0.0 |
Immingham |
1.0 |
Doncaster |
2.0 |
London |
3.0 |
Here, the cost is the cumulative total for relationships (or hops). This is the same path as we see using Breadth First Search in Spark.
We could even work out the total distance of following this path by writing a bit of postprocessing Cypher. The following procedure calculates the shortest unweighted path and then works out what the actual cost of that path would be:
MATCH(source:Place {id:"Amsterdam"}),(destination:Place {id:"London"})CALL gds.alpha.shortestPath.stream({startNode: source,endNode: destination,nodeProjection:"*",relationshipProjection: {all: {type:"*",orientation:"UNDIRECTED"}}})YIELD nodeId, costWITHcollect(gds.util.asNode(nodeId))ASpathUNWINDrange(0, size(path)-1)ASindexWITHpath[index]AScurrent, path[index+1]ASnextWITHcurrent, next, [(current)-[r:EROAD]-(next) | r.distance][0]ASdistanceWITHcollect({current: current, next:next, distance: distance})ASstopsUNWINDrange(0, size(stops)-1)ASindexWITHstops[index]ASlocation, stops, indexRETURNlocation.current.idASplace,reduce(acc=0.0,distancein[stopinstops[0..index] | stop.distance] |acc + distance)AScost;
If the previous code feels a bit unwieldy, notice that the tricky part is figuring out how to massage the data to include the cost over the whole journey. This is helpful to keep in mind when we need the cumulative path cost.
The query returns the following result:
| place | cost |
|---|---|
Amsterdam |
0.0 |
Immingham |
369.0 |
Doncaster |
443.0 |
London |
720.0 |
Figure 4-6 shows the unweighted shortest path from Amsterdam to London, routing us through the fewest number of cities. It has a total cost of 720 km.

Figure 4-6. The unweighted shortest path between Amsterdam and London
Choosing a route with the fewest number of nodes visited might be very useful in situations such as subway systems, where less stops are highly desirable. However, in a driving scenario, we’re probably more interested in the total cost using the shortest weighted path.
Shortest Path (Weighted) with Neo4j
We can execute the Weighted Shortest Path algorithm to find the shortest path between Amsterdam and London like this:
MATCH(source:Place {id:"Amsterdam"}),(destination:Place {id:"London"})CALL gds.alpha.shortestPath.stream({startNode: source,endNode: destination,nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}},relationshipWeightProperty:"distance"})YIELD nodeId, costRETURNgds.util.asNode(nodeId).idASplace, cost;
We are now passing the optional relationshipWeightProperty, which is the name of the relationship property that indicates the cost of traversing between a pair of nodes.
The cost is the number of kilometers between two locations. The query returns the following result:
| place | cost |
|---|---|
Amsterdam |
0.0 |
Den Haag |
59.0 |
Hoek van Holland |
86.0 |
Felixstowe |
293.0 |
Ipswich |
315.0 |
Colchester |
347.0 |
London |
453.0 |
The quickest route takes us via Den Haag, Hoek van Holland, Felixstowe, Ipswich, and Colchester! The cost shown is the cumulative total as we progress through the cities. First we go from Amsterdam to Den Haag, at a cost of 59. Then we go from Den Haag to Hoek van Holland, at a cumulative cost of 86—and so on. Finally, we arrive in London, from Colchester, for a total cost of 453 km.
Remember that the unweighted shortest path had a total cost of 720 km, so we’ve been able to save 267 km by taking weights into account when computing the shortest path.
Shortest Path (Weighted) with Apache Spark
In the Breadth First Search with Apache Spark section we learned how to find the shortest path between two nodes. That shortest path was based on hops and therefore isn’t the same as the shortest weighted path, which would tell us the shortest total distance between cities.
If we want to find the shortest weighted path (in this case, distance) we need to use the cost property, which is used for various types of weighting.
This option is not available out of the box with GraphFrames, so we need to write our own version of Weighted Shortest Path using its aggregateMessages framework. Most of our algorithm examples for Spark use the simpler process of calling on algorithms from the library, but we have the option of writing our own functions.
More information on aggregateMessages can be found in the “Message passing via AggregateMessages” section of the GraphFrames user guide.
Tip
When available, we recommend leveraging preexisting, tested libraries. Writing our own functions, especially for more complicated algorithms, requires a deeper understanding of our data and calculations.
The following example should be treated as a reference implementation, and would need to be optimized before running on a larger dataset. Those that aren’t interested in writing their own functions can skip this example.
Before we create our function, we’ll import some libraries that we’ll use:
fromgraphframes.libimportAggregateMessagesasAMfrompyspark.sqlimportfunctionsasF
The aggregateMessages module is part of the GraphFrames library and contains some useful helper functions.
Now let’s write our function. We first create a user-defined function that we’ll use to build the paths between our source and destination:
add_path_udf=F.udf(lambdapath,id:path+[id],ArrayType(StringType()))
And now for the main function, which calculates the shortest path starting from an origin and returns as soon as the destination has been visited:
defshortest_path(g,origin,destination,column_name="cost"):ifg.vertices.filter(g.vertices.id==destination).count()==0:return(spark.createDataFrame(sc.emptyRDD(),g.vertices.schema).withColumn("path",F.array()))vertices=(g.vertices.withColumn("visited",F.lit(False)).withColumn("distance",F.when(g.vertices["id"]==origin,0).otherwise(float("inf"))).withColumn("path",F.array()))cached_vertices=AM.getCachedDataFrame(vertices)g2=GraphFrame(cached_vertices,g.edges)whileg2.vertices.filter('visited == False').first():current_node_id=g2.vertices.filter('visited == False').sort("distance").first().idmsg_distance=AM.edge[column_name]+AM.src['distance']msg_path=add_path_udf(AM.src["path"],AM.src["id"])msg_for_dst=F.when(AM.src['id']==current_node_id,F.struct(msg_distance,msg_path))new_distances=g2.aggregateMessages(F.min(AM.msg).alias("aggMess"),sendToDst=msg_for_dst)new_visited_col=F.when(g2.vertices.visited|(g2.vertices.id==current_node_id),True).otherwise(False)new_distance_col=F.when(new_distances["aggMess"].isNotNull()&(new_distances.aggMess["col1"]<g2.vertices.distance),new_distances.aggMess["col1"]).otherwise(g2.vertices.distance)new_path_col=F.when(new_distances["aggMess"].isNotNull()&(new_distances.aggMess["col1"]<g2.vertices.distance),new_distances.aggMess["col2"].cast("array<string>")).otherwise(g2.vertices.path)new_vertices=(g2.vertices.join(new_distances,on="id",how="left_outer").drop(new_distances["id"]).withColumn("visited",new_visited_col).withColumn("newDistance",new_distance_col).withColumn("newPath",new_path_col).drop("aggMess","distance","path").withColumnRenamed('newDistance','distance').withColumnRenamed('newPath','path'))cached_new_vertices=AM.getCachedDataFrame(new_vertices)g2=GraphFrame(cached_new_vertices,g2.edges)ifg2.vertices.filter(g2.vertices.id==destination).first().visited:return(g2.vertices.filter(g2.vertices.id==destination).withColumn("newPath",add_path_udf("path","id")).drop("visited","path").withColumnRenamed("newPath","path"))return(spark.createDataFrame(sc.emptyRDD(),g.vertices.schema).withColumn("path",F.array()))
Warning
If we store references to any DataFrames in our functions, we need to cache them using the AM.getCachedDataFrame function or we’ll encounter a memory leak during execution.
In the shortest_path function we use this function to cache the vertices and new_vertices DataFrames.
If we wanted to find the shortest path between Amsterdam and Colchester we could call that function like so:
result=shortest_path(g,"Amsterdam","Colchester","cost")result.select("id","distance","path").show(truncate=False)
which would return the following result:
| id | distance | path |
|---|---|---|
Colchester |
347.0 |
[Amsterdam, Den Haag, Hoek van Holland, Felixstowe, Ipswich, Colchester] |
The total distance of the shortest path between Amsterdam and Colchester is 347 km and takes us via Den Haag, Hoek van Holland, Felixstowe, and Ipswich. By contrast, the shortest path in terms of number of relationships between the locations, which we worked out with the Breadth First Search algorithm (refer back to Figure 4-4), would take us via Immingham, Doncaster, and London.
Shortest Path Variation: A*
The A* Shortest Path algorithm improves on Dijkstra’s by finding shortest paths more quickly. It does this by allowing the inclusion of extra information that the algorithm can use, as part of a heuristic function, when determining which paths to explore next.
The algorithm was invented by Peter Hart, Nils Nilsson, and Bertram Raphael and described in their 1968 paper “A Formal Basis for the Heuristic Determination of Minimum Cost Paths”.
The A* algorithm operates by determining which of its partial paths to expand at each iteration of its main loop. It does so based on an estimate of the cost (heuristic) still left to reach the goal node.
Warning
Be thoughtful in the heuristic employed to estimate path costs. Underestimating path costs may unnecessarily include some paths that could have been eliminated, but the results will still be accurate. However, if the heuristic overestimates path costs, it may skip over actual shorter paths (incorrectly estimated to be longer) that should have been evaluated, which can lead to inaccurate results.
A* selects the path that minimizes the following function:
`f(n) = g(n) + h(n)`
where:
-
g(n)is the cost of the path from the starting point to noden. -
h(n)is the estimated cost of the path from nodento the destination node, as computed by a heuristic.
Note
In Neo4j’s implementation, geospatial distance is used as the heuristic. In our example transportation dataset we use the latitude and longitude of each location as part of the heuristic function.
A* with Neo4j
Neo4j’s A* algorithm takes in a config map with the following keys:
startNode-
The node where our shortest path search begins.
endNode-
The node where our shortest path search ends.
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
relationshipWeightProperty-
The relationship property that indicates the cost of traversing between a pair of nodes. The cost is the number of kilometers between two locations.
propertyKeyLat-
The name of the node property used to represent the latitude of each node as part of the geospatial heuristic calculation.
propertyKeyLon-
The name of the node property used to represent the longitude of each node as part of the geospatial heuristic calculation.
The following query executes the A* algorithm to find the shortest path between Den Haag and London:
MATCH(source:Place {id:"Den Haag"}),(destination:Place {id:"London"})CALL gds.alpha.shortestPath.astar.stream({startNode: source,endNode: destination,nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}},relationshipWeightProperty:"distance",propertyKeyLat:"latitude",propertyKeyLon:"longitude"})YIELD nodeId, costRETURNgds.util.asNode(nodeId).idASplace, cost;
Running this procedure gives the following result:
| place | cost |
|---|---|
Den Haag |
0.0 |
Hoek van Holland |
27.0 |
Felixstowe |
234.0 |
Ipswich |
256.0 |
Colchester |
288.0 |
London |
394.0 |
We’d get the same result using the Shortest Path algorithm, but on more complex datasets the A* algorithm will be faster as it evaluates fewer paths.
Shortest Path Variation: Yen’s k-Shortest Paths
Yen’s k-Shortest Paths algorithm is similar to the Shortest Path algorithm, but rather than finding just the shortest path between two pairs of nodes, it also calculates the second shortest path, third shortest path, and so on up to k-1 deviations of shortest paths.
Jin Y. Yen invented the algorithm in 1971 and described it in “Finding the K Shortest Loopless Paths in a Network”. This algorithm is useful for getting alternative paths when finding the absolute shortest path isn’t our only goal. It can be particularly helpful when we need more than one backup plan!
Yen’s with Neo4j
The Yen’s algorithm takes in a config map with the following keys:
startNode-
The node where our shortest path search begins.
endNode-
The node where our shortest path search ends.
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
relationshipWeightProperty-
The relationship property that indicates the cost of traversing between a pair of nodes. The cost is the number of kilometers between two locations.
k-
The maximum number of shortest paths to find.
The following query executes Yen’s algorithm to find the shortest paths between Gouda and Felixstowe:
MATCH(start:Place {id:"Gouda"}),(end:Place {id:"Felixstowe"})CALL gds.alpha.kShortestPaths.stream({startNode:start,endNode: end,nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}},relationshipWeightProperty:"distance",k: 5})YIELD index, sourceNodeId, targetNodeId, nodeIds, costs, pathRETURNindex,[node ingds.util.asNodes(nodeIds[1..-1]) |node.id]ASvia,reduce(acc=0.0, costincosts | acc + cost)AStotalCost;
After we get back the shortest paths, we look up the associated node for each node ID using the gds.util.asNodes function, and then filter out the start and end nodes from the resulting collection.
We also calculate the total cost for each path by summing the returned costs.
Running this procedure gives the following result:
| index | via | totalCost |
|---|---|---|
0 |
[Rotterdam, Hoek van Holland] |
265.0 |
1 |
[Den Haag, Hoek van Holland] |
266.0 |
2 |
[Rotterdam, Den Haag, Hoek van Holland] |
285.0 |
3 |
[Den Haag, Rotterdam, Hoek van Holland] |
298.0 |
4 |
[Utrecht, Amsterdam, Den Haag, Hoek van Holland] |
374.0 |
Figure 4-7 shows the shortest path between Gouda and Felixstowe.

Figure 4-7. The shortest path between Gouda and Felixstowe
The shortest path in Figure 4-7 is interesting in comparison to the results ordered by total cost. It illustrates that sometimes you may want to consider several shortest paths or other parameters. In this example, the second-shortest route is only 1 km longer than the shortest one. If we prefer the scenery, we might choose the slightly longer route.
All Pairs Shortest Path
The All Pairs Shortest Path (APSP) algorithm calculates the shortest (weighted) path between all pairs of nodes. It’s more efficient than running the Single Source Shortest Path algorithm for every pair of nodes in the graph.
APSP optimizes operations by keeping track of the distances calculated so far and running on nodes in parallel. Those known distances can then be reused when calculating the shortest path to an unseen node. You can follow the example in the next section to get a better understanding of how the algorithm works.
Note
Some pairs of nodes might not be reachable from each other, which means that there is no shortest path between these nodes. The algorithm doesn’t return distances for these pairs of nodes.
A Closer Look at All Pairs Shortest Path
The calculation for APSP is easiest to understand when you follow a sequence of operations. The diagram in Figure 4-8 walks through the steps for node A.
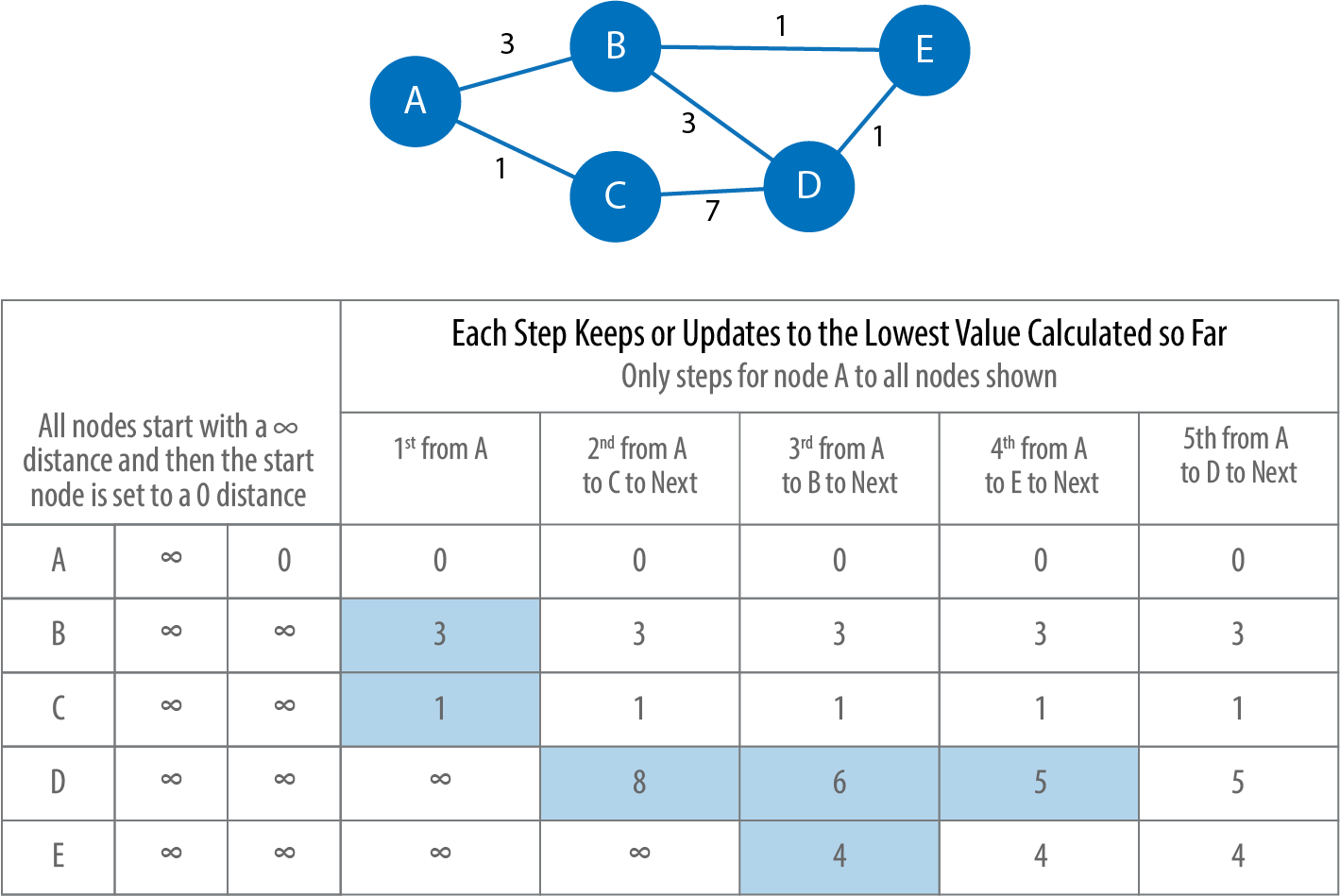
Figure 4-8. The steps to calculate the shortest path from node A to all other nodes, with updates shaded.
Initially the algorithm assumes an infinite distance to all nodes. When a start node is selected, then the distance to that node is set to 0. The calculation then proceeds as follows:
-
From start node A we evaluate the cost of moving to the nodes we can reach and update those values. Looking for the smallest value, we have a choice of B (cost of 3) or C (cost of 1). C is selected for the next phase of traversal.
-
Now from node C, the algorithm updates the cumulative distances from A to nodes that can be reached directly from C. Values are only updated when a lower cost has been found:
A=0, B=3, C=1, D=8, E=∞
-
Then B is selected as the next closest node that hasn’t already been visited. It has relationships to nodes A, D, and E. The algorithm works out the distance to those nodes by summing the distance from A to B with the distance from B to each of those nodes. Note that the lowest cost from the start node A to the current node is always preserved as a sunk cost. The distance (d) calculation results:
d(A,A) = d(A,B) + d(B,A) = 3 + 3 = 6 d(A,D) = d(A,B) + d(B,D) = 3 + 3 = 6 d(A,E) = d(A,B) + d(B,E) = 3 + 1 = 4
-
In this step the distance from node A to B and back to A, shown as d(A,A) = 6, is greater than the shortest distance already computed (0), so its value is not updated.
-
The distances for nodes D (6) and E (4) are less than the previously calculated distances, so their values are updated.
-
-
E is selected next. Only the cumulative total for reaching D (5) is now lower, and therefore it is the only one updated.
-
When D is finally evaluated, there are no new minimum path weights; nothing is updated, and the algorithm terminates.
When Should I Use All Pairs Shortest Path?
All Pairs Shortest Path is commonly used for understanding alternate routing when the shortest route is blocked or becomes suboptimal. For example, this algorithm is used in logical route planning to ensure the best multiple paths for diversity routing. Use All Pairs Shortest Path when you need to consider all possible routes between all or most of your nodes.
Example use cases include:
-
Optimizing the location of urban facilities and the distribution of goods. One example of this is determining the traffic load expected on different segments of a transportation grid. For more information, see R. C. Larson and A. R. Odoni’s book, Urban Operations Research (Prentice-Hall).
-
Finding a network with maximum bandwidth and minimal latency as part of a data center design algorithm. There are more details about this approach in the paper “REWIRE: An Optimization-Based Framework for Data Center Network Design”, by A. R. Curtis et al.
All Pairs Shortest Path with Apache Spark
Spark’s shortestPaths function is designed for finding the shortest paths from all nodes to a set of nodes called landmarks.
If we wanted to find the shortest path from every location to Colchester, Immingham, and Hoek van Holland, we would write the following query:
result=g.shortestPaths(["Colchester","Immingham","Hoek van Holland"])result.sort(["id"]).select("id","distances").show(truncate=False)
If we run that code in pyspark we’ll see this output:
| id | distances |
|---|---|
Amsterdam |
[Immingham → 1, Hoek van Holland → 2, Colchester → 4] |
Colchester |
[Colchester → 0, Hoek van Holland → 3, Immingham → 3] |
Den Haag |
[Hoek van Holland → 1, Immingham → 2, Colchester → 4] |
Doncaster |
[Immingham → 1, Colchester → 2, Hoek van Holland → 4] |
Felixstowe |
[Hoek van Holland → 1, Colchester → 2, Immingham → 4] |
Gouda |
[Hoek van Holland → 2, Immingham → 3, Colchester → 5] |
Hoek van Holland |
[Hoek van Holland → 0, Immingham → 3, Colchester → 3] |
Immingham |
[Immingham → 0, Colchester → 3, Hoek van Holland → 3] |
Ipswich |
[Colchester → 1, Hoek van Holland → 2, Immingham → 4] |
London |
[Colchester → 1, Immingham → 2, Hoek van Holland → 4] |
Rotterdam |
[Hoek van Holland → 1, Immingham → 3, Colchester → 4] |
Utrecht |
[Immingham → 2, Hoek van Holland → 3, Colchester → 5] |
The number next to each location in the distances column is the number of relationships (roads) between cities we need to traverse to get there from the source node. In our example, Colchester is one of our destination cities and you can see it has 0 nodes to traverse to get to itself but 3 hops to make from Immingham and Hoek van Holland. If we were planning a trip, we could use this information to help maximize our time at our chosen destinations.
All Pairs Shortest Path with Neo4j
Neo4j has a parallel implementation of the All Pairs Shortest Path algorithm, which returns the distance between every pair of nodes.
The All Pairs Shortest Path algorithm takes in a config map with the following keys:
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
relationshipWeightProperty-
The relationship property that indicates the cost of traversing between a pair of nodes. The cost is the number of kilometers between two locations.
If we don’t set relationshipWeightProperty then the algorithm will calculate the unweighted shortest paths between all pairs of nodes.
The following query does this:
CALL gds.alpha.allShortestPaths.stream({nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}}})YIELD sourceNodeId, targetNodeId, distanceWHEREsourceNodeId < targetNodeIdRETURNgds.util.asNode(sourceNodeId).idASsource,gds.util.asNode(targetNodeId).idAStarget,distanceORDER BYdistanceDESCLIMIT10;
This algorithm returns the shortest path between every pair of nodes twice—once with each of the nodes as the source node. This would be helpful if you were evaluating a directed graph of one-way streets.
However, we don’t need to see each path twice, so we filter the results to only keep one of them by using the sourceNodeId < targetNodeId predicate.
The query returns the following results:
| source | target | distance |
|---|---|---|
Colchester |
Utrecht |
5.0 |
London |
Rotterdam |
5.0 |
London |
Gouda |
5.0 |
Ipswich |
Utrecht |
5.0 |
Colchester |
Gouda |
5.0 |
Colchester |
Den Haag |
4.0 |
London |
Utrecht |
4.0 |
London |
Den Haag |
4.0 |
Colchester |
Amsterdam |
4.0 |
Ipswich |
Gouda |
4.0 |
This output shows the 10 pairs of locations that have the most relationships between them because we asked for results in descending order (DESC).
If we want to calculate the shortest weighted paths, we should set relationshipWeightProperty to the property name that contains the cost to be used in the shortest path calculation.
This property will then be evaluated to work out the shortest weighted path between each pair of nodes.
The following query does this:
CALL gds.alpha.allShortestPaths.stream({nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}},relationshipWeightProperty:"distance"})YIELD sourceNodeId, targetNodeId, distanceWHEREsourceNodeId < targetNodeIdRETURNgds.util.asNode(sourceNodeId).idASsource,gds.util.asNode(targetNodeId).idAStarget,distanceORDER BYdistanceDESCLIMIT10;
The query returns the following result:
| source | target | distance |
|---|---|---|
Doncaster |
Hoek van Holland |
529.0 |
Rotterdam |
Doncaster |
528.0 |
Gouda |
Doncaster |
524.0 |
Felixstowe |
Immingham |
511.0 |
Den Haag |
Doncaster |
502.0 |
Ipswich |
Immingham |
489.0 |
Utrecht |
Doncaster |
489.0 |
London |
Utrecht |
460.0 |
Colchester |
Immingham |
457.0 |
Immingham |
Hoek van Holland |
455.0 |
Now we’re seeing the 10 pairs of locations furthest from each other in terms of the total distance between them. Notice that Doncaster shows up frequently along with several cities in the Netherlands. It looks like it would be a long drive if we wanted to take a road trip between those areas.
Single Source Shortest Path
The Single Source Shortest Path (SSSP) algorithm, which came into prominence at around the same time as Dijkstra’s Shortest Path algorithm, acts as an implementation for both problems.
The SSSP algorithm calculates the shortest (weighted) path from a root node to all other nodes in the graph, as demonstrated in Figure 4-9.

Figure 4-9. The steps of the Single Source Shortest Path algorithm
It proceeds as follows:
-
It begins with a root node from which all paths will be measured. In Figure 4-9 we’ve selected node A as the root.
-
The relationship with the smallest weight coming from that root node is selected and added to the tree, along with its connected node. In this case, that’s d(A,D)=1.
-
The next relationship with the smallest cumulative weight from our root node to any unvisited node is selected and added to the tree in the same way. Our choices in Figure 4-9 are d(A,B)=8, d(A,C)=5 directly or 4 via A-D-C, and d(A,E)=5. So, the route via A-D-C is chosen and C is added to our tree.
-
The process continues until there are no more nodes to add and we have our single source shortest path.
When Should I Use Single Source Shortest Path?
Use Single Source Shortest Path when you need to evaluate the optimal route from a fixed start point to all other individual nodes. Because the route is chosen based on the total path weight from the root, it’s useful for finding the best path to each node, but not necessarily when all nodes need to be visited in a single trip.
For example, SSSP is helpful for identifying the main routes to use for emergency services where you don’t visit every location on each incident, but not for finding a single route for garbage collection where you need to visit each house in one trip. (In the latter case, you’d use the Minimum Spanning Tree algorithm, covered later.)
Example use cases include:
-
Detecting changes in topology, such as link failures, and suggesting a new routing structure in seconds
-
Using Dijkstra as an IP routing protocol for use in autonomous systems such as a local area network (LAN)
Single Source Shortest Path with Apache Spark
We can adapt the shortest_path function that we wrote to calculate the shortest path between two locations to instead return us the shortest path from one location to all others. Note that we’re using Spark’s aggregateMessages framework again to customize our function.
We’ll first import the same libraries as before:
fromgraphframes.libimportAggregateMessagesasAMfrompyspark.sqlimportfunctionsasF
And we’ll use the same user-defined function to construct paths:
add_path_udf=F.udf(lambdapath,id:path+[id],ArrayType(StringType()))
Now for the main function, which calculates the shortest path starting from an origin:
defsssp(g,origin,column_name="cost"):vertices=g.vertices\.withColumn("visited",F.lit(False))\.withColumn("distance",F.when(g.vertices["id"]==origin,0).otherwise(float("inf")))\.withColumn("path",F.array())cached_vertices=AM.getCachedDataFrame(vertices)g2=GraphFrame(cached_vertices,g.edges)whileg2.vertices.filter('visited == False').first():current_node_id=g2.vertices.filter('visited == False').sort("distance").first().idmsg_distance=AM.edge[column_name]+AM.src['distance']msg_path=add_path_udf(AM.src["path"],AM.src["id"])msg_for_dst=F.when(AM.src['id']==current_node_id,F.struct(msg_distance,msg_path))new_distances=g2.aggregateMessages(F.min(AM.msg).alias("aggMess"),sendToDst=msg_for_dst)new_visited_col=F.when(g2.vertices.visited|(g2.vertices.id==current_node_id),True).otherwise(False)new_distance_col=F.when(new_distances["aggMess"].isNotNull()&(new_distances.aggMess["col1"]<g2.vertices.distance),new_distances.aggMess["col1"])\.otherwise(g2.vertices.distance)new_path_col=F.when(new_distances["aggMess"].isNotNull()&(new_distances.aggMess["col1"]<g2.vertices.distance),new_distances.aggMess["col2"].cast("array<string>"))\.otherwise(g2.vertices.path)new_vertices=g2.vertices.join(new_distances,on="id",how="left_outer")\.drop(new_distances["id"])\.withColumn("visited",new_visited_col)\.withColumn("newDistance",new_distance_col)\.withColumn("newPath",new_path_col)\.drop("aggMess","distance","path")\.withColumnRenamed('newDistance','distance')\.withColumnRenamed('newPath','path')cached_new_vertices=AM.getCachedDataFrame(new_vertices)g2=GraphFrame(cached_new_vertices,g2.edges)returng2.vertices\.withColumn("newPath",add_path_udf("path","id"))\.drop("visited","path")\.withColumnRenamed("newPath","path")
If we want to find the shortest path from Amsterdam to all other locations we can call the function like this:
via_udf=F.udf(lambdapath:path[1:-1],ArrayType(StringType()))
result=sssp(g,"Amsterdam","cost")(result.withColumn("via",via_udf("path")).select("id","distance","via").sort("distance").show(truncate=False))
We define another user-defined function to filter out the start and end nodes from the resulting path. If we run that code we’ll see the following output:
| id | distance | via |
|---|---|---|
Amsterdam |
0.0 |
[] |
Utrecht |
46.0 |
[] |
Den Haag |
59.0 |
[] |
Gouda |
81.0 |
[Utrecht] |
Rotterdam |
85.0 |
[Den Haag] |
Hoek van Holland |
86.0 |
[Den Haag] |
Felixstowe |
293.0 |
[Den Haag, Hoek van Holland] |
Ipswich |
315.0 |
[Den Haag, Hoek van Holland, Felixstowe] |
Colchester |
347.0 |
[Den Haag, Hoek van Holland, Felixstowe, Ipswich] |
Immingham |
369.0 |
[] |
Doncaster |
443.0 |
[Immingham] |
London |
453.0 |
[Den Haag, Hoek van Holland, Felixstowe, Ipswich, Colchester] |
In these results we see the physical distances in kilometers from the root node, Amsterdam, to all other cities in the graph, ordered by shortest distance.
Single Source Shortest Path with Neo4j
Neo4j implements a variation of SSSP, called the Delta-Stepping algorithm that divides Dijkstra’s algorithm into a number of phases that can be executed in parallel.
The Single Source Shortest Path algorithm takes in a config map with the following keys:
startNode-
The node where our shortest path search begins.
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
relationshipWeightProperty-
The relationship property that indicates the cost of traversing between a pair of nodes. The cost is the number of kilometers between two locations.
delta-
The grade of concurrency to use
The following query executes the Delta-Stepping algorithm:
MATCH(n:Place {id:"London"})CALL gds.alpha.shortestPath.deltaStepping.stream({startNode: n,nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}},relationshipWeightProperty:"distance",delta: 1.0})YIELD nodeId, distanceWHEREgds.util.isFinite(distance)RETURNgds.util.asNode(nodeId).idASdestination, distanceORDER BYdistance;
The query returns the following output:
| destination | distance |
|---|---|
London |
0.0 |
Colchester |
106.0 |
Ipswich |
138.0 |
Felixstowe |
160.0 |
Doncaster |
277.0 |
Immingham |
351.0 |
Hoek van Holland |
367.0 |
Den Haag |
394.0 |
Rotterdam |
400.0 |
Gouda |
425.0 |
Amsterdam |
453.0 |
Utrecht |
460.0 |
In these results we see the physical distances in kilometers from the root node, London, to all other cities in the graph, ordered by shortest distance.
Minimum Spanning Tree
The Minimum (Weight) Spanning Tree algorithm starts from a given node and finds all its reachable nodes and the set of relationships that connect the nodes together with the minimum possible weight. It traverses to the next unvisited node with the lowest weight from any visited node, avoiding cycles.
The first known Minimum Weight Spanning Tree algorithm was developed by the Czech scientist Otakar Borůvka in 1926. Prim’s algorithm, invented in 1957, is the simplest and best known.
Prim’s algorithm is similar to Dijkstra’s Shortest Path algorithm, but rather than minimizing the total length of a path ending at each relationship, it minimizes the length of each relationship individually. Unlike Dijkstra’s algorithm, it tolerates negative-weight relationships.
The Minimum Spanning Tree algorithm operates as demonstrated in Figure 4-10.

Figure 4-10. The steps of the Minimum Spanning Tree algorithm
The steps are as follows:
-
It begins with a tree containing only one node. In Figure 4-10 we start with node A.
-
The relationship with smallest weight coming from that node is selected and added to the tree (along with its connected node). In this case, A-D.
-
This process is repeated, always choosing the minimal-weight relationship that joins any node not already in the tree. If you compare our example here to the SSSP example in Figure 4-9 you’ll notice that in the fourth graph the paths become different. This is because SSSP evaluates the shortest path based on cumulative totals from the root, whereas Minimum Spanning Tree only looks at the cost of the next step.
-
When there are no more nodes to add, the tree is a minimum spanning tree.
There are also variants of this algorithm that find the maximum-weight spanning tree (highest-cost tree) and the k-spanning tree (tree size limited).
When Should I Use Minimum Spanning Tree?
Use Minimum Spanning Tree when you need the best route to visit all nodes. Because the route is chosen based on the cost of each next step, it’s useful when you must visit all nodes in a single walk. (Review the previous section on “Single Source Shortest Path” if you don’t need a path for a single trip.)
You can use this algorithm for optimizing paths for connected systems like water pipes and circuit design. It’s also employed to approximate some problems with unknown compute times, such as the Traveling Salesman Problem and certain types of rounding problems. Although it may not always find the absolute optimal solution, this algorithm makes potentially complicated and compute-intensive analysis much more approachable.
Example use cases include:
-
Minimizing the travel cost of exploring a country. “An Application of Minimum Spanning Trees to Travel Planning” describes how the algorithm analyzed airline and sea connections to do this.
-
Visualizing correlations between currency returns. This is described in “Minimum Spanning Tree Application in the Currency Market”.
-
Tracing the history of infection transmission in an outbreak. For more information, see “Use of the Minimum Spanning Tree Model for Molecular Epidemiological Investigation of a Nosocomial Outbreak of Hepatitis C Virus Infection”.
Warning
The Minimum Spanning Tree algorithm only gives meaningful results when run on a graph where the relationships have different weights. If the graph has no weights, or all relationships have the same weight, then any spanning tree is a minimum spanning tree.
Minimum Spanning Tree with Neo4j
Let’s see the Minimum Spanning Tree algorithm in action. The Minimum Spanning Tree algorithm takes in a config map with the following keys:
startNodeId-
The id of the node where our shortest path search begins.
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
relationshipWeightProperty-
The relationship property that indicates the cost of traversing between a pair of nodes. The cost is the number of kilometers between two locations.
writeProperty-
The name of the relationship type written back as a result
weightWriteProperty-
The name of the weight property on the
writePropertyrelationship type written back
The following query finds a spanning tree starting from Amsterdam:
MATCH(n:Place {id:"Amsterdam"})CALL gds.alpha.spanningTree.minimum.write({startNodeId:id(n),nodeProjection:"*",relationshipProjection: {EROAD: {type:"EROAD",properties:"distance",orientation:"UNDIRECTED"}},relationshipWeightProperty:"distance",writeProperty:'MINST',weightWriteProperty:'cost'})YIELD createMillis, computeMillis, writeMillis, effectiveNodeCountRETURNcreateMillis, computeMillis, writeMillis, effectiveNodeCount;
The parameters passed to this algorithm are:
Place-
The node labels to consider when computing the spanning tree
EROAD-
The relationship types to consider when computing the spanning tree
distance-
The name of the relationship property that indicates the cost of traversing between a pair of nodes
id(n)-
The internal node id of the node from which the spanning tree should begin
This query stores its results in the graph. If we want to return the minimum weight spanning tree we can run the following query:
MATCHpath = (n:Place {id:"Amsterdam"})-[:MINST*]-()WITHrelationships(path)ASrelsUNWIND relsAS relWITH DISTINCT rel AS relRETURNstartNode(rel).idASsource,endNode(rel).idASdestination,rel.costAScost;
And this is the output of the query:
| source | destination | cost |
|---|---|---|
Amsterdam |
Utrecht |
46.0 |
Utrecht |
Gouda |
35.0 |
Gouda |
Rotterdam |
25.0 |
Rotterdam |
Den Haag |
26.0 |
Den Haag |
Hoek van Holland |
27.0 |
Hoek van Holland |
Felixstowe |
207.0 |
Felixstowe |
Ipswich |
22.0 |
Ipswich |
Colchester |
32.0 |
Colchester |
London |
106.0 |
London |
Doncaster |
277.0 |
Doncaster |
Immingham |
74.0 |
If we were in Amsterdam and wanted to visit every other place in our dataset during the same trip, Figure 4-11 demonstrates the shortest continuous route to do so.

Figure 4-11. A minimum weight spanning tree from Amsterdam
Random Walk
The Random Walk algorithm provides a set of nodes on a random path in a graph. The term was first mentioned by Karl Pearson in 1905 in a letter to Nature magazine titled “The Problem of the Random Walk”. Although the concept goes back even further, it’s only more recently that random walks have been applied to network science.
A random walk, in general, is sometimes described as being similar to how a drunk person traverses a city. They know what direction or end point they want to reach but may take a very circuitous route to get there.
The algorithm starts at one node and somewhat randomly follows one of the relationships forward or backward to a neighbor node. It then does the same from that node and so on, until it reaches the set path length. (We say somewhat randomly because the number of relationships a node has, and its neighbors have, influences the probability a node will be walked through.)
When Should I Use Random Walk?
Use the Random Walk algorithm as part of other algorithms or data pipelines when you need to generate a mostly random set of connected nodes.
Example use cases include:
-
As part of the node2vec and graph2vec algorithms, that create node embeddings. These node embeddings could then be used as the input to a neural network.
-
As part of the Walktrap and Infomap community detection. If a random walk returns a small set of nodes repeatedly, then it indicates that node set may have a community structure.
-
As part of the training process of machine learning models. This is described further in David Mack’s article “Review Prediction with Neo4j and TensorFlow”.
You can read about more use cases in a paper by N. Masuda, M. A. Porter, and R. Lambiotte, “Random Walks and Diffusion on Networks”.
Random Walk with Neo4j
Neo4j has an implementation of the Random Walk algorithm. It supports two modes for choosing the next relationship to follow at each stage of the algorithm:
random-
Randomly chooses a relationship to follow
node2vec-
Chooses relationship to follow based on computing a probability distribution of the previous neighbors
The Random Walk procedure takes in a config map with the following keys:
start-
The id of the node where our shortest path search begins.
nodeProjection-
Enables the mapping of specific kinds of nodes into the in-memory graph. We can declare one or more node labels.
relationshipProjection-
Enables the mapping of relationship types into the in-memory graph. We can declare one or more relationship types along with direction and properties.
walks-
The number of paths returned ``
The following performs a random walk starting from London:
MATCH(source:Place {id:"London"})CALL gds.alpha.randomWalk.stream({start:id(source),nodeProjection:"*",relationshipProjection: {all: {type:"*",properties:"distance",orientation:"UNDIRECTED"}},steps: 5,walks: 1})YIELD nodeIdsUNWIND gds.util.asNodes(nodeIds)asplaceRETURNplace.idASplace
It returns the following result:
| place |
|---|
London |
Doncaster |
Immingham |
Amsterdam |
Utrecht |
Amsterdam |
At each stage of the random walk the next relationship is chosen randomly. This means that if we rerun the algorithm, even with the same parameters, we likely won’t get the same result. It’s also possible for a walk to go back on itself, as we can see in Figure 4-12 where we go from Amsterdam to Den Haag and back.

Figure 4-12. A random walk starting from London
Summary
Pathfinding algorithms are useful for understanding the way that our data is connected. In this chapter we started out with the fundamental Breadth and Depth First algorithms, before moving onto Dijkstra and other shortest path algorithms. We also looked at variants of the shortest path algorithms optimized for finding the shortest path from one node to all other nodes or between all pairs of nodes in a graph. We finished with the Random Walk algorithm, which can be used to find arbitrary sets of paths.
Next we’ll learn about Centrality algorithms that can be used to find influential nodes in a graph.
Get Graph Algorithms now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

