Fundamentos de la calidad de datos

Capítulo 4. Monitoreo y detección de anomalías para tus conductos de datos

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

Con Ryan Kearns

Imagina que acabas de comprar un coche nuevo. Según la comprobación rutinaria previa a la compra, todos los sistemas funcionan según el manual, los depósitos de aceite y líquido de frenos están llenos casi hasta el borde y las piezas están como nuevas, porque, bueno, lo están.

Después de coger las llaves del concesionario, te pones en marcha. "No hay nada como el olor a coche nuevo", piensas mientras entras en la autopista. Todo va bien hasta que oyes un fuerte estallido. ¡Caramba! Y tu coche empieza a tambalearse. Te detienes en el arcén, enciendes las luces de emergencia y saltas del coche. Tras una breve investigación, has identificado al presunto culpable del fuerte sonido: un neumático pinchado. Por muchas pruebas o comprobaciones que haya podido hacer el concesionario para validar la salud de tu coche, no se pueden tener en cuenta incógnitas desconocidas (por ejemplo, clavos o escombros en la carretera) que puedan afectar a tu vehículo.

Del mismo modo, en los datos, todas las pruebas y comprobaciones de calidad de datos bajo el sol no pueden protegerte totalmente del tiempo de inactividad de los datos, que puede manifestarse en todas las etapas del proceso y surgir por diversas razones que a menudo no están relacionadas con los propios datos.

Cuando se trata de comprender cuándo se rompen los datos, lo mejor que puedes hacer es apoyarte en el monitoreo, concretamente en técnicas de detección de anomalías que identifiquen cuándo tus umbrales previstos de volumen, frescura, distribución y otros valores no cumplen las expectativas.

La detección de anomalías se refiere a la identificación de sucesos u observaciones que se desvían de la norma: por ejemplo, un comportamiento fraudulento con una tarjeta de crédito o un fallo técnico, como la caída de un sitio web. Suponiendo que tu sitio web funcione normalmente, claro.

Existen varias técnicas, algoritmos y marcos de trabajo que utilizan (y desarrollan) gigantes del sector como Meta, Google, Uber y otros. Para una profundización técnica, recomendamos el informe de Preetam Jinka y Baron Schwartz Anomaly Detection for Monitoring (O'Reilly).

Hasta hace poco, la detección de anomalías se consideraba un "nice-to-have" -no una necesidad- para muchos equipos de datos. Ahora, a medida que los sistemas de datos se hacen cada vez más complejos y las empresas facultan a los empleados de todas las funciones para utilizar los datos, es imperativo que los equipos adopten enfoques tanto proactivos como reactivos para resolver la calidad de los datos.

Aunque los automóviles son muy diferentes de las tuberías de datos, los coches y otros sistemas mecánicos también tienen sus propias capacidades de monitoreo y detección de anomalías. La mayoría de los vehículos actuales te avisan cuando el aceite, el líquido de frenos, la gasolina, la presión de los neumáticos y otras entidades vitales están más bajos de lo que deberían y te animan a actuar. El monitoreo de datos y la detección de anomalías funcionan de forma muy parecida.

En este capítulo, veremos cómo construir tus propios monitores de calidad de datos para un entorno de almacén de datos, con el fin de monitorizar y alertar sobre los pilares de la observabilidad de los datos: frescura, volumen, distribución y esquema. En el proceso, introduciremos conceptos y términos importantes, necesarios para aumentar tu comprensión de importantes técnicas de detección de anomalías.

Conocer tus incógnitas conocidas y tus incógnitas desconocidas

En este mundo hay dos tipos de problemas de calidad de datos: los que puedes predecir (desconocidos conocidos) y los que no (desconocidos desconocidos). Los desconocidos conocidos son problemas que puedes predecir fácilmente, es decir, valores nulos, problemas específicos de frescura o cambios de esquema provocados por un sistema que se actualiza con regularidad. Puede que estos problemas no se produzcan, pero con una buena dosis de pruebas, a menudo puedes tenerlos en cuenta antes de que causen problemas aguas abajo. En la Figura 4-1, destacamos ejemplos populares de ambas cosas.

Las incógnitas desconocidas se refieren al tiempo de inactividad de los datos que ni siquiera las pruebas más exhaustivas pueden tener en cuenta, problemas que surgen en toda tu cadena de datos, no sólo en las secciones cubiertas por pruebas específicas. Los desconocidos pueden ser:

• Una anomalía de distribución en un campo crítico que hace que tu panel de Tableau funcione mal

• Un cambio en el esquema JSON realizado por otro equipo que convierte 6 columnas en 600

• Un cambio involuntario en el ETL (o en el ETL inverso, si te apetece) que hace que las pruebas no se ejecuten y se pierdan datos erróneos

• Datos incompletos o anticuados que pasan desapercibidos hasta varias semanas después, afectando a las métricas clave de marketing

• Un cambio de código que hace que una API deje de recoger datos que alimentan un nuevo producto importante

• Desviación de los datos a lo largo del tiempo, que puede ser difícil de detectar, sobre todo si tus pruebas sólo tienen en cuenta los datos que se están escribiendo en el momento de tus trabajos ETL, que normalmente no tienen en cuenta los datos que ya están en una tabla determinada.

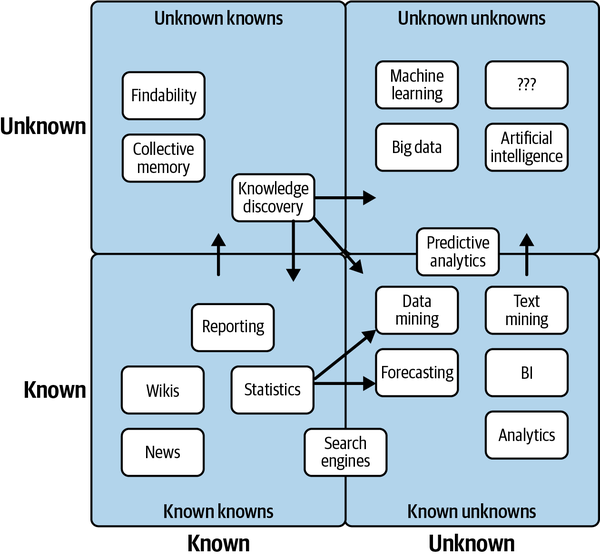
Figura 4-1. Ejemplos de incógnitas conocidas e incógnitas desconocidas

Mientras que las pruebas y los disyuntores pueden manejar muchas de tus incógnitas conocidas, el monitoreo y la detección de anomalías pueden cubrir tus bases cuando se trata de incógnitas desconocidas.

Con frecuencia, los equipos de datos aprovechan el monitoreo y la detección de anomalías para identificar y alertar sobre el comportamiento de los datos que se desvía de lo que se espera históricamente de una determinada canalización de datos. Al comprender qué aspecto tienen los datos "buenos", es más fácil identificar proactivamente los datos "malos".

Ahora que hemos esbozado las diferencias entre estos dos tipos de problemas de datos, vamos a sumergirnos en cómo es en la práctica la detección de anomalías para desconocidos.

Construir un algoritmo de detección de anomalías

Para cristalizar cómo funciona la detección de anomalías, vamos a recorrer un tutorial del mundo real en la construcción de un detector de anomalías para un conjunto de datos muy anómalos.

Ten en cuenta que puedes utilizar un gran número de tecnologías y enfoques para crear monitores de calidad de datos, y que las opciones que elijas dependerán de tu pila tecnológica. En este ejemplo, utilizamos los siguientes lenguajes y herramientas:

• SQLite y SQL

• Cuadernos Jupyter

• Python

Nuestro ecosistema de datos de muestra utiliza datos astronómicos simulados sobre exoplanetas habitables. A efectos de este ejercicio, hemos generado el conjunto de datos con Python, modelando anomalías de incidentes reales que nos hemos encontrado en entornos de producción. Este conjunto de datos es de uso totalmente gratuito, y la carpetautils del repositorio contiene el código que generó los datos, por si te interesa saber más sobre cómo se ensamblaron.

Utilizaremos SQLite 3.32.3, que debería permitir acceder a la base de datos desde el símbolo del sistema o desde archivos SQL con una configuración mínima. Los conceptos se extienden realmente a cualquier lenguaje de consulta, y estas implementaciones pueden ampliarse a MySQL, Snowflake y otros entornos de bases de datos con cambios mínimos.

A continuación, compartimos información de tablas sobre nuestro conjunto de datos EXOPLANETS, incluidas cinco entradas específicas de la base de datos:

$ sqlite3 EXOPLANETS.db
sqlite> PRAGMA TABLE_INFO(EXOPLANETS);
_id            | TEXT | 0 | | 0  
distance       | REAL | 0 | | 0  
g              | REAL | 0 | | 0  
orbital_period | REAL | 0 | | 0  
avg_temp       | REAL | 0 | | 0  
date_added     | TEXT | 0 | | 0  

Una entrada de la base de datos en EXOPLANETS contiene la siguiente información:

_id: un UUID correspondiente al planeta

distancedistancia a la Tierra, en años luz

ggravedad superficial como múltiplo de g, la constante de la fuerza gravitatoria

orbital_period: duración de un ciclo orbital en días

avg_temptemperatura media de la superficie en grados Kelvin

date_added: la fecha en que nuestro sistema descubrió el planeta y lo añadió automáticamente a nuestras bases de datos

Ten en cuenta que uno o más de distance, g, orbital_period, y avg_temp pueden ser NULL para un planeta determinado como consecuencia de la falta de datos o de datos erróneos.

Si consultamos sqlite> SELECT * FROM EXOPLANETS LIMIT 5;, podemos extraer cinco filas de nuestra base de datos. En el Ejemplo 4-1, compartimos cinco entradas de la base de datos en nuestro conjunto de datos EXOPLANETS, para destacar el formato y la distribución de los datos.

Ejemplo 4-1. Cinco filas del conjunto de datos EXOPLANETS

_id,distance,g,orbital_period,avg_temp,date_added
c168b188-ef0c-4d6a-8cb2-f473d4154bdb,34.6273036348341,,476.480044083599, ...
e7b56e84-41f4-4e62-b078-01b076cea369,110.196919810563,2.52507362359066, ...
a27030a0-e4b4-4bd7-8d24-5435ed86b395,26.6957950454452,10.2764970016067, ...
54f9cf85-eae9-4f29-b665-855357a14375,54.8883521129783,,173.788967912197, ...
4d06ec88-f5c8-4d03-91ef-7493a12cd89e,153.264217159834,0.922874568459221, ...

Ten en cuenta que este ejercicio es retroactivo: estamos analizando datos históricos. En un entorno de datos de producción, la detección de anomalías es en tiempo real y se aplica en cada etapa del ciclo de vida de los datos, por lo que implicará una implementación ligeramente distinta a la que se hace aquí.

A efectos de este ejercicio, construiremos algoritmos de observabilidad de datos para la frescura y la distribución, pero en futuros artículos abordaremos el resto de nuestros cinco pilares, y más.

Monitoreo de la frescura

El primer pilar de la observabilidad de los datos que monitorizamos es la frescura, que puede darnos un fuerte indicador de cuándo se actualizaron por última vez los activos de datos críticos. Si un informe que se actualiza regularmente cada hora de repente parece muy anticuado, este tipo de anomalía debería darnos un fuerte indicio de que algo es inexacto o está mal.

En primer lugar, fíjate en la columna DATE_ADDED. SQL no almacena metadatos sobre cuándo se añaden registros individuales. Así que, para visualizar la frescura en esta configuración retroactiva, tenemos que rastrear esa información nosotros mismos. Agrupar por la columna DATE_ADDED puede darnos una idea de cómo se actualiza diariamente EXOPLANETS. Como se muestra en el Ejemplo 4-2, podemos consultar el número de nuevos ID añadidos al día.

Ejemplo 4-2. Una consulta sobre el número de nuevos exoplanetas añadidos a nuestro conjunto de datos por día

SELECT
  DATE_ADDED,
  COUNT(*) AS ROWS_ADDED
FROM
  EXOPLANETS
GROUP BY
  DATE_ADDED;

Puedes ejecutarlo tú mismo con $ sqlite3 EXOPLANETS.db < queries/freshness/rows-added.sql en el repositorio. Obtendremos de vuelta los datos del Ejemplo 4-3.

Ejemplo 4-3. Datos extraídos del Ejemplo 4-2

date_added     ROWS_ADDED
2020-01-01     84
2020-01-02     92
2020-01-03     101
2020-01-04     102
2020-01-05     100
... ...
2020-07-14     104
2020-07-15     110
2020-07-16     103
2020-07-17     89
2020-07-18     104

Según esta representación gráfica de nuestro conjunto de datos, parece que EXOPLANETS se actualiza constantemente con unas 100 entradas nuevas cada día, aunque hay lagunas en las que no llegan datos durante varios días.

Recuerda que, con la frescura, queremos preguntarnos "¿Están mis datos actualizados?"; por lo tanto, conocer esos vacíos en las actualizaciones de las tablas es esencial para comprender la fiabilidad de nuestros datos. La siguiente consulta, Ejemplo 4-4, operacionaliza la frescura (como se muestra en la Figura 4-2) introduciendo una métrica para DAYS_SINCE_LAST_UPDATE. (Nota: dado que este tutorial utiliza SQLite3, la sintaxis SQL para calcular las diferencias de tiempo será diferente en MySQL, Snowflake y otros entornos).

Ejemplo 4-4. Consulta que extrae el número de días transcurridos desde la actualización del conjunto de datos

WITH UPDATES AS(
  SELECT
    DATE_ADDED,
    COUNT(*) AS ROWS_ADDED
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
)
  
SELECT
  DATE_ADDED,
  JULIANDAY(DATE_ADDED) - JULIANDAY(LAG(DATE_ADDED) OVER(
    ORDER BY DATE_ADDED
  )) AS DAYS_SINCE_LAST_UPDATE
FROM
  UPDATES;

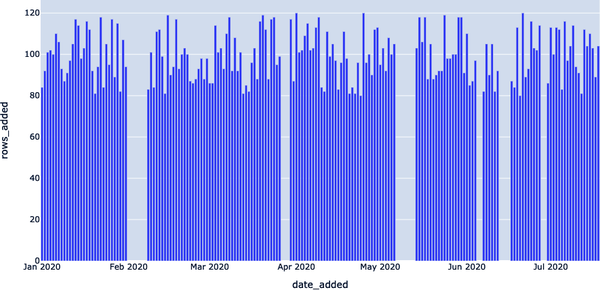
Figura 4-2. Representación de patrones de frescura en nuestro conjunto de datos utilizando un cuaderno Jupyter

La tabla resultante, Ejemplo 4-5, dice: "En la fecha X, los datos más recientes en EXOPLANETS tenían Y días". Se trata de información no disponible explícitamente en la columna DATE_ADDED de la tabla, pero la aplicación de la observabilidad de los datos nos proporciona las herramientas para descubrirla. Esto se visualiza en la Figura 4-3, donde las anomalías de frescura se representan por los altos valores de Y. Esto denota retrasos en la actualización de la tabla, que podemos consultar con un simple detector.

Ejemplo 4-5. Tabla de frescura de datos de exoplanetas a partir de la consulta del Ejemplo 4-4

DATE_ADDED     DAYS_SINCE_LAST_UPDATE
2020–01–01     
2020–01–02     1
2020–01–03     1
2020–01–04     1
2020–01–05     1
...            ...
2020–07–14     1
2020–07–15     1
2020–07–16     1
2020–07–17     1
2020–07–18     1

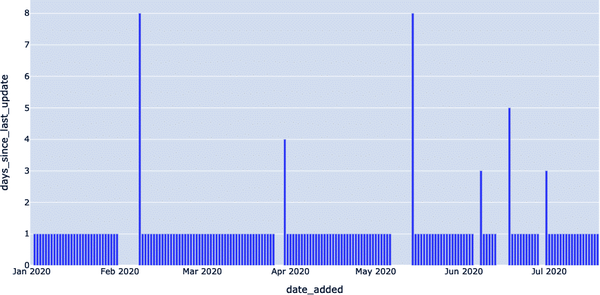
Figura 4-3. Visualización de las anomalías de frescura representadas por valores Y elevados

Ahora tenemos los datos que necesitamos para detectar anomalías de frescura. Sólo nos queda establecer un parámetro de umbral para Y: ¿cuántos días de antigüedad son demasiados? Un parámetro convierte una consulta, Ejemplo 4-6, en un detector, ya que decide lo que cuenta como anómalo (léase: digno de alerta) y lo que no.

Ejemplo 4-6. Consulta modificada para alertar de datos que se sitúan más allá de la frescura esperada para datos de exoplanetas

WITH UPDATES AS(
  SELECT
    DATE_ADDED,
    COUNT(*) AS ROWS_ADDED
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
),
  
NUM_DAYS_UPDATES AS (
  SELECT
    DATE_ADDED,
    JULIANDAY(DATE_ADDED) - JULIANDAY(LAG(DATE_ADDED)
      OVER(
        ORDER BY DATE_ADDED
      )
    ) AS DAYS_SINCE_LAST_UPDATE
  FROM
    UPDATES
)
  
SELECT
  *
FROM
  NUM_DAYS_UPDATES
WHERE
  DAYS_SINCE_LAST_UPDATE > 1;

Los datos que se nos devuelven, Ejemplo 4-7, representan fechas en las que se produjeron incidentes de frescura.

Ejemplo 4-7. Datos obtenidos de la consulta del Ejemplo 4-6

DATE_ADDED     DAYS_SINCE_LAST_UPDATE
2020–02–08     8
2020–03–30     4
2020–05–14     8
2020–06–07     3
2020–06–17     5
2020–06–30     3

En 2020-05-14, ¡los datos más recientes de la tabla tenían 8 días! Una interrupción de este tipo puede representar una rotura en nuestra canalización de datos y sería bueno conocerla si estamos utilizando estos datos para algo de alto impacto (y si estamos utilizando esto en un entorno de producción, lo más probable es que lo estemos haciendo). Como se ilustra en la Figura 4-4, podemos representar anomalías de frescura estableciendo umbrales para lo que es una cantidad aceptable de tiempo desde la última actualización.

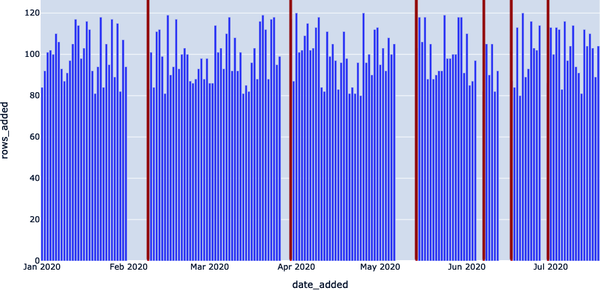
Figura 4-4. Visualización de anomalías de frescura mediante umbrales

Fíjate especialmente en la última línea de la consulta: DAYS_SINCE_LAST_UPDATE > 1;.

Aquí, 1 es un parámetro del modelo: no hay nada "correcto" en este número, aunque cambiarlo influirá en las fechas que consideremos incidentes. Cuanto menor sea el número, más anomalías auténticas detectaremos (alta recuperación), pero lo más probable es que varias de estas "anomalías" no reflejen cortes reales. Cuanto mayor sea el número, mayor será la probabilidad de que todas las anomalías que captemos reflejen anomalías verdaderas (alta precisión), pero es posible que pasemos por alto algunas.

A efectos de este ejemplo, podríamos cambiar 1 por 7 y así capturar sólo las dos peores interrupciones (el 2020-02-08 y el 2020-05-14). Cualquier elección aquí reflejará el caso de uso y los objetivos particulares; es un equilibrio importante que surge una y otra vez al aplicar la observabilidad de datos a escala a entornos de producción .

En la Figura 4-5, utilizamos el mismo detector de frescura, pero con la consulta SQLite DAYS_SINCE_LAST_UPDATE > 3; como umbral. Ahora dos de las interrupciones más pequeñas no se detectan.

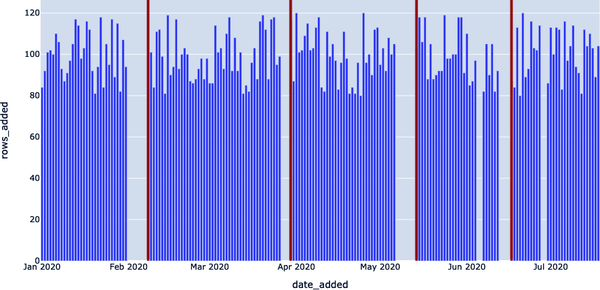
Figura 4-5. Acotar la búsqueda de anomalías (DAYS_SINCE_LAST_UPDATE > 3)

Ahora, visualizamos el mismo detector de frescura, pero con DAYS_SINCE_LAST_UPDATE > 7; sirviendo ahora como umbral. Todas las interrupciones, excepto las dos más grandes, pasan ahora desapercibidas(Figura 4-6).

Al igual que los planetas, los parámetros óptimos de los modelos se sitúan en una "Zona Ricitos de Oro" o "punto dulce" entre los valores considerados demasiado bajos y demasiado altos.

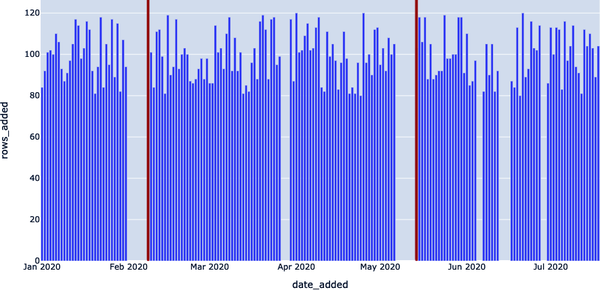
Figura 4-6. Acotar más la búsqueda de anomalías (DAYS_SINCE_LAST_UPDATE > 7 )

Comprender la distribución

A continuación, queremos evaluar la salud distributiva de nuestros datos a nivel de campo. La distribución nos indica todos los valores esperados de nuestros datos, así como la frecuencia con que se produce cada valor. Una de las preguntas más sencillas es: "¿Con qué frecuencia son NULOS mis datos?". En muchos casos, cierto nivel de datos incompletos es aceptable, pero si una tasa de nulos del 10% se convierte en un 90%, querremos saberlo.

En estadística, nos gusta suponer que los conjuntos de observaciones se extraen de distribuciones base que obedecen reglas matemáticas. Llamamos a las primeras "distribuciones muestrales" y a las segundas "distribuciones verdaderas". La estadística tiene una observación sobre los procesos naturales, llamada teorema del límite central, que afirma que las distribuciones de muestras aleatorias generadas independientemente se aproximan a una determinada distribución a medida que el número de muestras aumenta.

Teorema del límite central

El teorema del límite central sugiere que si tienes una muestra suficientemente aleatoria de un conjunto de datos dado con media μ y desviación típica σ, entonces la distribución de las medias muestrales tendrá una distribución aproximadamente normal.

La distribución normal, o distribución gaussiana -la famosa curva de campana que todos conocemos de la clase de estadística, mostrada en la Figura 4-7- puedeindicarnos cuál es el comportamiento normal de un conjunto de datos determinado. Las gaussianas pueden resumirse muy bien con dos variables -su media, μ, y su varianza, σ-, loque las hace potentes y omnipresentes en el análisis estadístico.

Figura 4-7. Una distribución normal (gaussiana) representa la forma más básica de detección de anomalías (ojalá fuera así de fácil)

Aplicar la distribución gaussiana puede dar lugar a un primer enfoque de la detección de anomalías bastante ingenuo, pero sorprendentemente eficaz: calcular la puntuación estándar de cada observación. Es decir, restar μ y luego dividir por σ. Esta puntuación (también llamada puntuación z) proporciona una métrica cuantificable de lo "alejada" (en la curva de campana) que está cada observación. Detección de anomalías: ¡resuelto! Basta con trazar una línea en algún punto fuera del centro de la campana y llamar "anómalo" a todo lo que quede fuera de esa línea. Desde un punto de vista estadístico, estarás en lo cierto. Por desgracia, la teoría estadística no es un enfoque convincente para la detección de anomalías en el campo muy concreto de la calidad de los datos, por dos razones.

En primer lugar, el teorema central del límite establece una característica clave del proceso de generación de datos que mucha gente pasa por alto: las observaciones independientes y aleatorias dan lugar a distribuciones normales en el límite. Se trata de una suposición estupenda para medir el volumen del viento a través de la hierba, o la longitud de la zancada del neoyorquino medio. No lo es tanto para los datos de inteligencia empresarial, donde las observaciones tienden a estar muy correlacionadas y confundidas con otras variables. Por ejemplo, los "clientes diarios" no se distribuirán normalmente en Chick-Fil-A, que cierra los domingos, ya que 1/7 de todas las observaciones serán 0. Estas observaciones no se generan aleatoriamente, sino que se ven afectadas por el día de la semana.

En segundo lugar, existe una distinción entre observaciones "anómalas" e "interesantes" que no puede captarse del todo con el pensamiento puramente estadístico. Para ilustrar esto, considera la puntuación z, como se ha comentado unos párrafos antes. Dijimos (en broma) que la detección de anomalías puede resolverse con una simple puntuación z; por desgracia, rara vez es así.

Si elegimos definir "anomalía" como cualquier cosa, digamos, tres desviaciones estándar de la media de la distribución, podemos tener la garantía de acertar en cualquier dato. Pero no sólo nos dedicamos a identificar métricas simplemente anómalas. Por un lado, nuestras series temporales contienen información contextual importante (¿Qué día de la semana era? ¿Se repite el patrón?). Pero lo más importante es que no todas las observaciones anómalas son interesantes: no nos ayudan a identificar y corregir el tiempo de inactividad de los datos. El ejemplo 4-8 consulta datos con una distribución anómala.

Ejemplo 4-8. Consulta para obtener datos sobre distribuciones anómalas

SELECT
  DATE_ADDED,
  CAST(
    SUM(
      CASE
        WHEN DISTANCE IS NULL THEN 1
        ELSE 0
      END
    ) AS FLOAT) / COUNT(*) AS DISTANCE_NULL_RATE,
  CAST(
    SUM(
      CASE
        WHEN G IS NULL THEN 1
        ELSE 0
      END
    ) AS FLOAT) / COUNT(*) AS G_NULL_RATE,
  CAST(
    SUM(
      CASE
        WHEN ORBITAL_PERIOD IS NULL THEN 1
        ELSE 0
      END
    ) AS FLOAT) / COUNT(*) AS ORBITAL_PERIOD_NULL_RATE,
  CAST(
    SUM(
      CASE
        WHEN AVG_TEMP IS NULL THEN 1
        ELSE 0
      END
    ) AS FLOAT) / COUNT(*) AS AVG_TEMP_NULL_RATE
FROM
  EXOPLANETS
GROUP BY
  DATE_ADDED;

Esta consulta devuelve muchos datos, como se muestra en el Ejemplo 4-9.

Ejemplo 4-9. Datos de la consulta del Ejemplo 4-8

date_added     DISTANCE_NULL_RATE    G_NULL_RATE          ORBITAL_PERIOD_NULL_RATE
2020-01-01     0.0833333333333333    0.178571428571429    0.214285714285714
2020-01-02     0.0                   0.152173913043478    0.326086956521739
2020-01-03     0.0594059405940594    0.188118811881188    0.237623762376238
2020-01-04     0.0490196078431373    0.117647058823529    0.264705882352941
...            ...                   ...                  ...
2020-07-13     0.0892857142857143    0.160714285714286    0.285714285714286
2020-07-14     0.0673076923076923    0.125                0.269230769230769
2020-07-15     0.0636363636363636    0.118181818181818    0.245454545454545
2020-07-16     0.058252427184466     0.145631067961165    0.262135922330097
2020-07-17     0.101123595505618     0.0898876404494382   0.247191011235955
2020-07-18     0.0673076923076923    0.201923076923077    0.317307692307692

La fórmula general CAST(SUM(CASE WHEN SOME_METRIC IS NULL THEN 1 ELSE 0 END) AS FLOAT) / COUNT(*), agrupada por la columna DATE_ADDED, nos está indicando la tasa de valores NULL para SOME_METRIC en los lotes diarios de datos nuevos en EXOPLANETS. Es difícil hacerse una idea mirando la salida en bruto, pero una visualización(Figura 4-8) puede ayudar a iluminar esta anomalía.

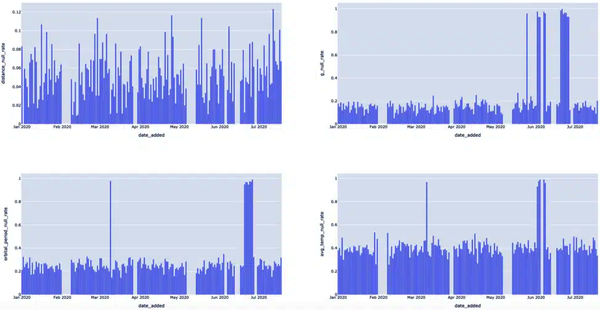
Figura 4-8. Al representar varios eventos provocados por tasas nulas, podemos ver claramente qué fechas eran anómalas

Los visuales dejan claro que hay eventos "pico" de tasa nula que deberíamos detectar. Centrémonos sólo en la última métrica, AVG_TEMP, por ahora. Podemos detectar los picos nulos más básicamente con un simple umbral mediante la consulta del Ejemplo 4-10.

Ejemplo 4-10. Detección de valores nulos en la columna AVG_TEMP del conjunto de datos EXOPLANETS

WITH NULL_RATES AS(
  SELECT
    DATE_ADDED,
    CAST(
      SUM(
        CASE
          WHEN AVG_TEMP IS NULL THEN 1
          ELSE 0
        END
      ) AS FLOAT) / COUNT(*) AS AVG_TEMP_NULL_RATE 
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
)
  
SELECT
  *
FROM
  NULL_RATES
WHERE
  AVG_TEMP_NULL_RATE  > 0.9;

En el Ejemplo 4-11, compartimos los datos correspondientes extraídos en su forma bruta, ilustrando las filas con valores nulos en la columna AVG_TEMP del conjunto de datos.

Ejemplo 4-11. AVG_TEMP filas con valores nulos

DATE_ADDED     AVG_TEMP_NULL_RATE
2020-03-09     0.967391304347826
2020-06-02     0.929411764705882
2020-06-03     0.977011494252874
2020-06-04     0.989690721649485
2020-06-07     0.987804878048781
2020-06-08     0.961904761904762

En la Figura 4-9, resaltamos dónde estaban los picos anómalos, correlacionados con la tasa de valores nulos en la columna de temperatura de nuestro conjunto de datos EXOPLANETS.

En lo que respecta a los algoritmos de detección, este método para identificar valores nulos es una especie de instrumento contundente. A veces, los patrones de nuestros datos serán lo suficientemente sencillos como para que un umbral como éste sirva. En otros casos, sin embargo, los datos serán ruidosos o tendrán otras complicaciones, como la estacionalidad, que nos obligarán a cambiar nuestro enfoque.

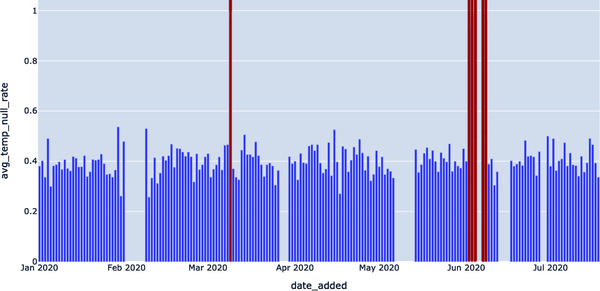
Figura 4-9. Detección de picos nulos en la temperatura media

Nota

La estacionalidad se refiere a la tendencia de una serie temporal a observar fluctuaciones predecibles en determinados intervalos. Por ejemplo, los datos de "asistentes a la iglesia" podrían observar una estacionalidad semanal con un alto sesgo hacia el domingo, y los datos de ventas de abrigos de unos grandes almacenes probablemente observarían una estacionalidad anual con un máximo en otoño y un mínimo en primavera.

Por ejemplo, detectar 2020-06-02, 2020-06-03 y 2020-06-04 parece redundante. Podemos filtrar las fechas que ocurren inmediatamente después de otras alertas para reducir la duplicación mediante la consulta del Ejemplo 4-12.

Ejemplo 4-12. Consulta para filtrar fechas que ocurren inmediatamente después de otras alertas

WITH NULL_RATES AS(
  SELECT
    DATE_ADDED,
    CAST(
      SUM(
        CASE
          WHEN AVG_TEMP IS NULL THEN 1
          ELSE 0
        END
      ) AS FLOAT
    ) / COUNT(*) AS AVG_TEMP_NULL_RATE
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
),
  
ALL_DATES AS (
  SELECT
    *,
    JULIANDAY(DATE_ADDED) - JULIANDAY(LAG(DATE_ADDED)
      OVER(
        ORDER BY DATE_ADDED
      )
    ) AS DAYS_SINCE_LAST_ALERT
  FROM
    NULL_RATES
  WHERE
    AVG_TEMP_NULL_RATE > 0.9
)
  
SELECT
  DATE_ADDED,
  AVG_TEMP_NULL_RATE
FROM
  ALL_DATES
WHERE
  DAYS_SINCE_LAST_ALERT IS NULL OR DAYS_SINCE_LAST_ALERT > 1;

El conjunto de datos correspondiente aparece en el Ejemplo 4-13. Estos resultados destacan las fechas que no es necesario tener en cuenta en nuestro detector de anomalías de valores nulos, según la consulta del Ejemplo 4-12.

Ejemplo 4-13. Resultados de la consulta del Ejemplo 4-12

DATE_ADDED     AVG_TEMP_NULL_RATE
2020-03-09     0.967391304347826
2020-06-02     0.929411764705882
2020-06-07     0.987804878048781

Observa que en ambas consultas, el parámetro clave es 0,9. En realidad estamos diciendo: "Cualquier tasa de nulos superior al 90% es un problema, y necesito saberlo". Visualizamos estos resultados en la Figura 4-10. Esto nos ayuda a reducir el ruido blanco y a generar resultados más precisos.

En este caso, podemos (y debemos) ser un poco más inteligentes aplicando el concepto de media móvil con un parámetro más inteligente utilizando la consulta del Ejemplo 4-14 para mejorar aún más la precisión.

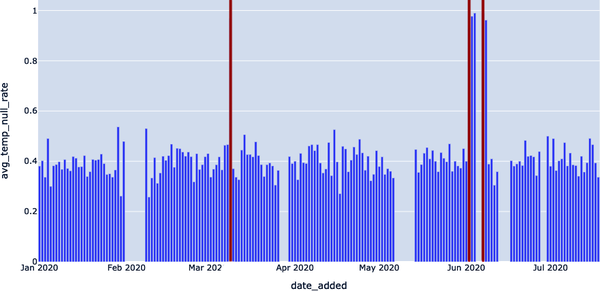
Figura 4-10. Visualizar cualquier tasa nula superior al 90%

Ejemplo 4-14. Consulta para aplicar una media móvil a la tasa nula

WITH NULL_RATES AS(
  SELECT
    DATE_ADDED,
    CAST(SUM(CASE WHEN AVG_TEMP IS NULL THEN 1 ELSE 0 END) AS FLOAT) / 
      COUNT(*) AS AVG_TEMP_NULL_RATE
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
),
  
NULL_WITH_AVG AS(
  SELECT
    *,
    AVG(AVG_TEMP_NULL_RATE) OVER (
      ORDER BY DATE_ADDED ASC
      ROWS BETWEEN 14 PRECEDING AND CURRENT ROW) AS TWO_WEEK_ROLLING_AVG
  FROM
    NULL_RATES
  GROUP BY
    DATE_ADDED
)
  
SELECT
  *
FROM
  NULL_WITH_AVG
WHERE
  AVG_TEMP_NULL_RATE - TWO_WEEK_ROLLING_AVG > 0.3;

Los resultados de la consulta se muestran en el Ejemplo 4-15 y se representan en la Figura 4-11. Vemos valores nulos que podrían hacer saltar alarmas mayores (es decir, con un porcentaje de nulos superior al 90%).

Ejemplo 4-15. Resultados de la consulta del Ejemplo 4-14

DATE_ADDED     AVG_TEMP_NULL_RATE    TWO_WEEK_ROLLING_AVG
2020-03-09     0.967391304347826     0.436077995611105
2020-06-02     0.929411764705882     0.441299602441599
2020-06-03     0.977011494252874     0.47913211475687
2020-06-04     0.989690721649485     0.515566041654715
2020-06-07     0.987804878048781     0.554753033524633
2020-06-08     0.961904761904762     0.594966974173356

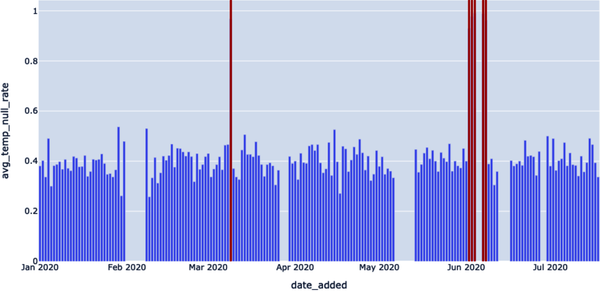
Figura 4-11. Utilizando la consulta AVG_TEMP_NULL_RATE — TWO_WEEK_ROLLING_AVG para ser aún más específico al identificar la tasa de valor nulo

Una aclaración: observa que filtramos utilizando la cantidad AVG_TEMP_NULL_RATE — TWO_WEEK_ROLLING_AVG. En otros casos, es posible que queramos tomar la ABS() de esta cantidad de error, pero no aquí; la razón es que un "pico" de tasa de nulos es mucho más alarmante si representa un aumento respecto a la media anterior. Puede que no merezca la pena monitorear siempre que los nulos disminuyan bruscamente de frecuencia, mientras que el valor de detectar un aumento de la tasa de nulos es claro.

Construir monitores para esquema y linaje

En la sección anterior, examinamos los dos primeros pilares de la observabilidad de los datos, la frescura y la distribución, y mostramos cómo un poco de código SQL puede hacer operativos estos conceptos. Se trata de lo que yo llamaría problemas más "clásicos" de detección de anomalías en los datos: dado un flujo constante de datos, ¿hay algo que parezca fuera de lugar?

Una buena detección de anomalías es sin duda parte del rompecabezas de la observabilidad de los datos, pero no lo es todo. Igualmente importante es el contexto. Si se ha producido una anomalía en los datos, estupendo. Pero, ¿dónde? ¿Qué conductos ascendentes pueden ser la causa? ¿Qué cuadros de mando descendentes se verán afectados por una anomalía de datos? ¿Y ha cambiado la estructura formal de mis datos? Una buena observabilidad de los datos depende de nuestra capacidad de aprovechar adecuadamente los metadatos para responder a estas preguntas sobre anomalías en los datos.

En nuestra siguiente sección, examinaremos los dos pilares de la observabilidad de los datos diseñados para responder a estas preguntas: el esquema y el linaje. Una vez más, utilizaremos herramientas ligeras como Jupyter y SQLite, para que puedas poner en marcha fácilmente nuestro entorno y probar tú mismo estos ejercicios de anomalías de datos. Comencemos.

Detección de anomalías para cambios de esquema y linaje

Como antes, trabajaremos con datos astronómicos simulados sobre exoplanetas habitables. Parece que nuestros datos más antiguos datan de 2020-01-01 (nota: la mayoría de las bases de datos no almacenan marcas de tiempo para registros individuales, así que nuestra columna DATE_ADDED lleva la cuenta por nosotros). Nuestros datos más recientes parecen ser del 2020-07-18:

sqlite> SELECT DATE_ADDED FROM EXOPLANETS ORDER BY DATE_ADDED DESC LIMIT 1; 
    2020-07-18

Por supuesto, se trata de la misma tabla que utilizamos en la sección anterior. Si queremos explorar los pilares más cargados de contexto del esquema y el linaje, tendremos que ampliar nuestro entorno.

Ahora, además de EXOPLANETS, tenemos una tabla llamada EXOPLANETS_EXTENDEDque es un superconjunto de nuestra tabla anterior. Es útil pensar que se trata de la misma tabla en distintos momentos del tiempo. De hecho, EXOPLANETS_EXTENDED tiene datos que se remontan al 2020-01-01:

sqlite> SELECT DATE_ADDED FROM EXOPLANETS_EXTENDED ORDER BY DATE_ADDED ASC 
    LIMIT 1; 2020-01-01

Pero también contiene datos hasta 2020-09-06, más allá de EXOPLANETS:

sqlite> SELECT DATE_ADDED FROM EXOPLANETS_EXTENDED ORDER BY DATE_ADDED DESC 
    LIMIT 1; 2020-09-0

Algo más es diferente entre estas tablas, como se muestra en el Ejemplo 4-16. Hay dos campos adicionales, lo que aumenta aún más la posibilidad de anomalías.

Ejemplo 4-16. Dos campos adicionales en el conjunto de datos EXOPLANETS_EXTENDED

sqlite> PRAGMA TABLE_INFO(EXOPLANETS_EXTENDED);
_ID             | VARCHAR(16777216)  | 1 | | 0
DISTANCE        | FLOAT              | 0 | | 0
G               | FLOAT              | 0 | | 0
ORBITAL_PERIOD  | FLOAT              | 0 | | 0
AVG_TEMP        | FLOAT              | 0 | | 0
DATE_ADDED      | TIMESTAMP_NTZ(6)   | 1 | | 0
ECCENTRICITY    | FLOAT              | 0 | | 0  
ATMOSPHERE      | VARCHAR(16777216)  | 0 | | 0  

Además de los seis campos de EXOPLANETS, la tabla EXOPLANETS_EXTENDED contiene dos campos adicionales:

ECCENTRICITYla excentricidad orbital del planeta alrededor de su estrella anfitriona

ATMOSPHEREla composición química dominante de la atmósfera del planeta

Ten en cuenta que, al igual que DISTANCE, G, ORBITAL_PERIOD, y AVG_TEMP, tanto ECCENTRICITY como ATMOSPHERE pueden ser NULL para un planeta determinado como consecuencia de la falta de datos o de datos erróneos. Por ejemplo, los planetas rebeldes tienen una excentricidad orbital indefinida y muchos planetas no tienen atmósfera.

Observa también que los datos no se rellenan, lo que significa que las entradas de datos del principio de la tabla (datos contenidos también en la tabla EXOPLANETS ) no tendrán información de excentricidad y atmósfera. En el Ejemplo 4-17, compartimos una consulta para resaltar que los datos antiguos no se rellenan; es de esperar que esto muestre el cambio de esquema que se produjo.

Ejemplo 4-17. Consulta que resalta que los datos antiguos no se rellenan

SELECT
 DATE_ADDED,
 ECCENTRICITY,
 ATMOSPHERE
FROM
 EXOPLANETS_EXTENDED
ORDER BY
 DATE_ADDED ASC
LIMIT 10;

Podemos hacer que este archivo sea bonito y que se puedan hacer búsquedas en él si se corrige este error: no se han encontrado comas en este archivo CSV en la línea 0 (representada en el Ejemplo 4-18).

Ejemplo 4-18. Adición de dos nuevas columnas, señal de un cambio de esquema en nuestro EXOPLANETS conjunto de datos

2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |
2020-01-01 | |

La adición de dos campos es un ejemplo de cambio de esquema: se ha modificado el plano formal de nuestros datos. Los cambios de esquema se producen cuando se altera la estructura de tus datos, y es una anomalía de los datos que puede ser frustrante depurar manualmente. Los cambios de esquema pueden indicar cualquier número de cosas sobre tus datos, incluyendo:

• La adición de nuevos puntos finales de la API

• Campos supuestamente obsoletos que aún no lo están

• La suma o resta de columnas, filas o tablas enteras

En un mundo ideal, nos gustaría tener un registro de este cambio, ya que representa un vector de posibles problemas con nuestra tubería. Por desgracia, nuestra base de datos no está configurada de forma natural para hacer un seguimiento de tales cambios. No tiene historial de versiones, como se muestra en el Ejemplo 4-19. Un cambio de esquema nos puede sorprender fácilmente.

Ejemplo 4-19. Sin historial de versiones en el conjunto de datos

sqlite> PRAGMA TABLE_INFO(EXOPLANETS_COLUMNS);
 
DATE    | TEXT | 0 | | 0
 
COLUMNS | TEXT | 0 | | 0

Nos encontramos con este problema al consultar la edad de registros individuales y añadimos la columna DATE_ADDED para solucionarlo. En este caso, haremos algo parecido, pero añadiendo una tabla entera.

La tabla EXOPLANETS_COLUMNS "versiona" nuestro esquema registrando las columnas en EXOPLANETS_EXTENDED en una fecha determinada. Si observamos la primera y la última entrada, vemos que las columnas cambiaron definitivamente en algún momento, como se destaca en el Ejemplo 4-20. Las dos entradas del Ejemplo 4-20 ponen de manifiesto que se han añadido dos nuevas columnas a nuestro conjunto de datos EXOPLANETS, es decir, que se ha producido un cambio de esquema.

Ejemplo 4-20. Dos entradas que destacan un cambio de esquema

sqlite> SELECT * FROM EXOPLANETS_COLUMNS ORDER BY DATE ASC LIMIT 1;
2020-01-01 | [
   (0, '_id', 'TEXT', 0, None, 0),
   (1, 'distance', 'REAL', 0, None, 0),
   (2, 'g', 'REAL', 0, None, 0),
   (3, 'orbital_period', 'REAL', 0, None, 0),
   (4, 'avg_temp', 'REAL', 0, None, 0),
   (5, 'date_added', 'TEXT', 0, None, 0)
 ]
 
sqlite> SELECT * FROM EXOPLANETS_COLUMNS ORDER BY DATE DESC LIMIT 1;
2020-09-06 | [
   (0, '_id', 'TEXT', 0, None, 0),
   (1, 'distance', 'REAL', 0, None, 0),
   (2, 'g', 'REAL', 0, None, 0),
   (3, 'orbital_period', 'REAL', 0, None, 0),
   (4, 'avg_temp', 'REAL', 0, None, 0),
   (5, 'date_added', 'TEXT', 0, None, 0),
   (6, 'eccentricity', 'REAL', 0, None, 0),
   (7, 'atmosphere', 'TEXT', 0, None, 0)
 ]

Ahora, volviendo a nuestra pregunta original: ¿cuándo, exactamente, cambió el esquema? Como nuestras listas de columnas están indexadas por fechas, podemos encontrar la fecha del cambio y una buena pista de dónde se encuentran las anomalías con un rápido script SQL, como se muestra en el Ejemplo 4-21.

Ejemplo 4-21. Una consulta de la tabla EXOPLANETS ampliada para mostrar cuándo cambió el esquema del conjunto de datos

WITH CHANGES AS(
 SELECT
   DATE,
   COLUMNS AS NEW_COLUMNS,
   LAG(COLUMNS) OVER(ORDER BY DATE) AS PAST_COLUMNS
 FROM
   EXOPLANETS_COLUMNS
)
 
SELECT
   *
FROM
   CHANGES
WHERE
   NEW_COLUMNS != PAST_COLUMNS
ORDER BY
   DATE ASC;

El Ejemplo 4-22 incluye los datos devueltos, que hemos reformateado para que sean legibles. Observando los datos, vemos que el esquema cambió el 2022-07-19.

Ejemplo 4-22. Resultados extraídos de la consulta del Ejemplo 4-21

DATE:          2020–07–19
NEW_COLUMNS:  [
               (0, '_id', 'TEXT', 0, None, 0),
               (1, 'distance', 'REAL', 0, None, 0),
               (2, 'g', 'REAL', 0, None, 0),
               (3, 'orbital_period', 'REAL', 0, None, 0),
               (4, 'avg_temp', 'REAL', 0, None, 0),
               (5, 'date_added', 'TEXT', 0, None, 0),
               (6, 'eccentricity', 'REAL', 0, None, 0),
               (7, 'atmosphere', 'TEXT', 0, None, 0)
          ]
PAST_COLUMNS: [
               (0, '_id', 'TEXT', 0, None, 0),
               (1, 'distance', 'REAL', 0, None, 0),
               (2, 'g', 'REAL', 0, None, 0),
               (3, 'orbital_period', 'REAL', 0, None, 0),
               (4, 'avg_temp', 'REAL', 0, None, 0),
               (5, 'date_added', 'TEXT', 0, None, 0)
          ]

Con esta consulta, devolvemos la fecha infractora: 2020-07-19. Al igual que la observabilidad de la frescura y la distribución, la observabilidad del esquema sigue un patrón: identificamos los metadatos útiles que señalan la salud de la tubería, los rastreamos y creamos detectores para alertarnos de posibles problemas. Proporcionar una tabla adicional como EXOPLANETS_COLUMNS es una forma de rastrear el esquema, pero hay muchas otras. Te animamos a que pienses en cómo podrías implementar un detector de cambios de esquema para tu propia canalización de datos.

Visualizar el linaje

Hemos descrito el linaje como el más holístico de los cinco pilares de la observabilidad de los datos, y con razón. El linaje contextualiza los incidentes indicándonos (1) qué fuentes descendentes pueden estar afectadas, y (2) qué fuentes ascendentes pueden ser la causa raíz. Aunque no es intuitivo "visualizar" el linaje con código SQL, un ejemplo rápido puede ilustrar cómo puede ser útil. (En el Capítulo 6, te enseñaremos a construir tu propio sistema de linaje a nivel de campo desde cero utilizando marcos comunes de código abierto).

Para demostrar cómo funciona, vamos a añadir otra tabla a nuestra base de datos. Hasta ahora, hemos estado registrando datos sobre exoplanetas. He aquí una pregunta divertida: ¿cuántos de estos planetas pueden albergar vida?

La tabla HABITABLES toma datos de EXOPLANETS para ayudarnos a responder a esa pregunta, entre otras características, como se muestra en el Ejemplo 4-23.

Ejemplo 4-23. HABITABLES proporciona información sobre si los planetas enumerados en EXOPLANETS son habitables

sqlite> PRAGMA TABLE_INFO(HABITABLES);
_id           | TEXT | 0 | | 0  
perihelion    | REAL | 0 | | 0  
aphelion      | REAL | 0 | | 0  
atmosphere    | TEXT | 0 | | 0  
habitability  | REAL | 0 | | 0  
min_temp      | REAL | 0 | | 0  
max_temp      | REAL | 0 | | 0  
date_added    | TEXT | 0 | | 0  

Una entrada en HABITABLES contiene lo siguiente:

_id: un UUID correspondiente al planeta

perihelion: la distancia más cercana al cuerpo celeste durante un periodo orbital

aphelion: la distancia más lejana al cuerpo celeste durante un periodo orbital

atmospherela composición química dominante de la atmósfera del planeta

habitability: un número real entre 0 y 1, que indica la probabilidad de que el planeta albergue vida

min_templa temperatura mínima en la superficie del planeta

max_temp: la temperatura máxima en la superficie del planeta

date_added: la fecha en que nuestro sistema descubrió el planeta y lo añadió automáticamente a nuestras bases de datos

Al igual que las columnas de EXOPLANETS, se permite que los valores de perihelion, aphelion, atmosphere, min_temp y max_temp sean NULL. De hecho, perihelion y aphelion serán NULL para cualquier _id en EXOPLANETS donde eccentricity sea NULL, ya que se utiliza la excentricidad orbital para calcular estas métricas. Esto explica por qué estos dos campos son siempre NULL en nuestras entradas de datos más antiguas.

Para ver qué exoplanetas son más habitables, podemos utilizar la siguiente consulta para obtener el resultado del Ejemplo 4-24:

sqlite> SELECT * FROM HABITABLES LIMIT 5;

Ejemplo 4-24. Salida de la consulta para obtener una idea de los exoplanetas más habitables

_id,perihelion,aphelion,atmosphere,habitability,min_temp,max_temp,date_added
c168b188-ef0c-4d6a-8cb2-f473d4154bdb,,,,0.291439672855434,,,2020-01-01
e7b56e84-41f4-4e62-b078-01b076cea369,,,,0.835647137991933,,,2020-01-01
a27030a0-e4b4-4bd7-8d24-5435ed86b395,,,,0.894000806332343,,,2020-01-01
54f9cf85-eae9-4f29-b665-855357a14375,,,,0.41590200852556,103.71374885412 ...
4d06ec88-f5c8-4d03-91ef-7493a12cd89e,,,,0.593524201489497,,,2020-01-01

Así, sabemos que HABITABLES depende de los valores de EXOPLANETS (o, lo que es lo mismo, de EXOPLANETS_EXTENDED), y EXOPLANETS_COLUMNS también. En la Figura 4-12 se muestra un gráfico de dependencias de nuestra base de datos.

Figura 4-12. Gráfico de dependencia que muestra el linaje entre los datos de origen y los "productos" posteriores

Información muy simple sobre el linaje, pero ya de por sí útil. Veamos una anomalía de datos en HABITABLES en el contexto de este gráfico, y veamos qué podemos aprender.

Investigar una anomalía en los datos

Cuando tenemos una métrica clave, como habitability en HABITABLES, podemos evaluar la salud de esa métrica de varias maneras. Para empezar, ¿cuál es el valor medio de habitability para los nuevos datos de un día determinado? En el Ejemplo 4-25, consultamos el valor medio de habitabilidad de los nuevos datos sobre exoplanetas.

Ejemplo 4-25. Consulta para obtener el valor medio de habitabilidad de los nuevos datos de exoplanetas

SELECT
  DATE_ADDED,
  AVG(HABITABILITY) AS AVG_HABITABILITY
FROM
  HABITABLES
GROUP BY
  DATE_ADDED;

El ejemplo 4-26 es el archivo CSV generado por la consulta.

Ejemplo 4-26. Resultados de la consulta del Ejemplo 4-25

DATE_ADDED,AVG_HABITABILITY
2020-01-01,0.435641365919993
2020-01-02,0.501288741945045
2020-01-03,0.512285861062438
2020-01-04,0.525461586113648
2020-01-05,0.528935065722722
...,...
2020-09-02,0.234269938329633
2020-09-03,0.26522042788867
2020-09-04,0.267919611991401
2020-09-05,0.298614978406792
2020-09-06,0.276007150628875

Observando estos datos, vemos que algo va mal. Parece que tenemos una anomalía en los datos. El valor medio de la habitabilidad suele estar en torno a 0,5, pero se reduce a la mitad, en torno a 0,25, más adelante en los datos registrados(Figura 4-13).

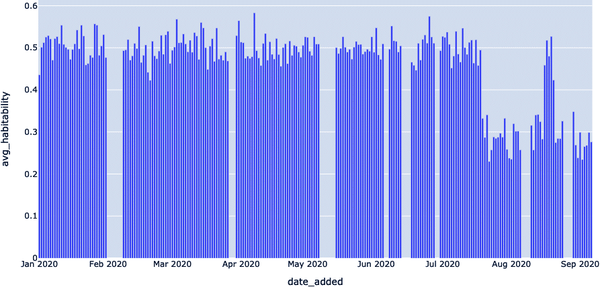
Figura 4-13. Visualizar el archivo CSV para comprender mejor dónde se produjo la anomalía en los datos y por qué

En la Figura 4-13, podemos ver claramente que se trata de una anomalía en la distribución de los datos, pero ¿qué ocurre exactamente? En otras palabras, ¿cuál es la causa de esta anomalía de los datos?

¿Por qué no miramos la tasa de nulos de habitabilidad, como hicimos al detectar anomalías de distribución anteriormente en el capítulo? Podemos hacerlo aprovechando la consulta del Ejemplo 4-27, que extrae la tasa de nulos de nuestro nuevo conjunto de datos ampliado, dándonos pistas sobre posibles anomalías en los datos.

Ejemplo 4-27. Consulta de tasa nula para un nuevo conjunto de datos

SELECT
 DATE_ADDED,
 CAST(
   SUM(
    CASE
    WHEN HABITABILITY IS NULL THEN 1
    ELSE 0
    END
   ) AS FLOAT) / COUNT(*) AS HABITABILITY_NULL_RATE
FROM
 HABITABLES
GROUP BY
 DATE_ADDED;

Afortunadamente, aquí nada parece fuera de lugar, como puedes ver en los resultados, resaltados en el Ejemplo 4-28.

Ejemplo 4-28. Resultados de la consulta del Ejemplo 4-27

DATE_ADDED,HABITABILITY_NULL_RATE
2020-01-01,0.0
2020-01-02,0.0
2020-01-03,0.0
2020-01-04,0.0
2020-01-05,0.0
...,...
2020-09-02,0.0
2020-09-03,0.0
2020-09-04,0.0
2020-09-05,0.0
2020-09-06,0.0

Como puedes ver en el Ejemplo 4-28, esto no parece prometedor como causa de nuestro problema. ¿Y si nos fijamos en otra métrica de salud de la distribución, la tasa de valores cero? Ésta es otra causa potencial de una anomalía en la distribución. Ejecutemos otra consulta, como se muestra en el Ejemplo 4-29, que nos ayude a hacer exactamente eso.

Ejemplo 4-29. Consulta para conocer la tasa de valores cero

SELECT
 DATE_ADDED,
 CAST(
   SUM(
    CASE
    WHEN HABITABILITY IS 0 THEN 1
    ELSE 0
    END
   ) AS FLOAT) / COUNT(*) AS HABITABILITY_ZERO_RATE
FROM
 HABITABLES
GROUP BY
 DATE_ADDED;

Evidentemente, aquí hay algo más que falla, como demuestra el archivo CSV representado en el Ejemplo 4-30. La habitabilidad de varios exoplanetas tiene un índice cero, lo que podría ser la causa de una anomalía en los datos.

Ejemplo 4-30. Resultados de la consulta del Ejemplo 4-29

DATE_ADDED,HABITABILITY_ZERO_RATE
2020-01-01,0.0
2020-01-02,0.0
2020-01-03,0.0
2020-01-04,0.0
2020-01-05,0.0
...,...
2020-09-02,0.442307692307692
2020-09-03,0.441666666666667
2020-09-04,0.466666666666667
2020-09-05,0.46218487394958
2020-09-06,0.391304347826087

En la Figura 4-14, visualizamos los resultados de nuestra consulta de tasa cero utilizando AS FLOAT) / COUNT (*) AS HABITABILITY_ZERO_RATE; esto ilustra los resultados anómalos en agosto y septiembre de 2020.

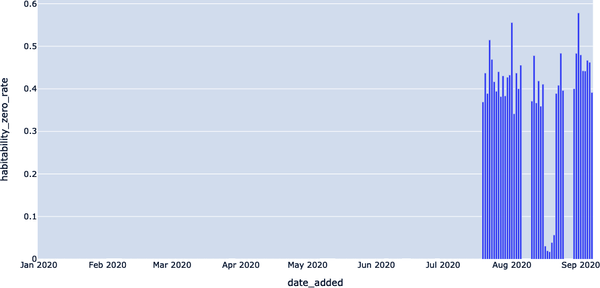
Figura 4-14. Visualización de las tasas de valor cero y la probable causa raíz de la anomalía

Podemos adaptar uno de los detectores de distribución que construimos anteriormente en el capítulo para obtener la primera fecha de tasas cero apreciables en el campo de la habitabilidad, como se muestra en el Ejemplo 4-31.

Ejemplo 4-31. Consulta de la primera fecha de tasas cero en el campo de habitabilidad

WITH HABITABILITY_ZERO_RATES AS(
  SELECT
    DATE_ADDED,
    CAST(
      SUM(
        CASE
          WHEN HABITABILITY IS 0 THEN 1
          ELSE 0
        END
      ) AS FLOAT) / COUNT(*) AS HABITABILITY_ZERO_RATE
  FROM
    HABITABLES
  GROUP BY
    DATE_ADDED
),
  
CONSECUTIVE_DAYS AS(
SELECT
  DATE_ADDED,
  HABITABILITY_ZERO_RATE,
  LAG(HABITABILITY_ZERO_RATE) OVER(ORDER BY DATE_ADDED) 
    AS PREV_HABITABILITY_ZERO_RATE
FROM
  HABITABILITY_ZERO_RATES
)
  
SELECT
  *
FROM
  CONSECUTIVE_DAYS
WHERE
  PREV_HABITABILITY_ZERO_RATE = 0 AND
  HABITABILITY_ZERO_RATE != 0;

A continuación, podemos ejecutar esta consulta a través de la línea de comandos del Ejemplo 4-32, que obtendrá la primera fecha de ceros apreciables en el campo de habitabilidad.

Ejemplo 4-32. Interfaz de línea de comandos que ejecuta la consulta del Ejemplo 4-31

$ sqlite3 EXOPLANETS.db < queries/lineage/habitability-zero-rate-detector.sql
DATE_ADDED | HABITABILITY_ZERO_RATE | PREV_HABITABILITY_ZERO_RATE
2020–07–19 | 0.369047619047619 | 0.0

2020-07-19 fue la primera fecha en que la tasa cero empezó a mostrar resultados anómalos. Recordemos que éste es el mismo día que la detección del cambio de esquema en EXOPLANETS_EXTENDED. EXOPLANETS_EXTENDED está aguas arriba de HABITABLES, por lo que es muy posible que estos dos incidentes estén relacionados.

De este modo, la información sobre el linaje puede ayudarnos a identificar la causa raíz de los incidentes y a avanzar más rápidamente hacia su resolución. Compara las dos explicaciones siguientes de este incidente en HABITABLES:

1. El 2020-07-19, el índice cero de la columna de habitabilidad de la tabla HABITABLES saltó del 0% al 37%.

2. El 2020-07-19, empezamos a rastrear dos campos adicionales, eccentricity y atmosphere, en la tabla EXOPLANETS. Esto tuvo un efecto adverso en la tabla descendente HABITABLES, estableciendo a menudo los campos min_temp y max_temp en valores extremos siempre que eccentricity no fuera NULL. A su vez, esto provocó un pico en la tasa cero del campo habitability, que detectamos como una disminución anómala del valor medio.

Desglosemos estas explicaciones. La explicación 1 utiliza sólo el hecho de que se produjo una anomalía en los datos. La explicación 2 utiliza el linaje, en términos de dependencias entre tablas y campos, para situar el incidente en su contexto y determinar la causa raíz. Todo en la segunda explicación es realmente correcto, y te animamos a que trastees con el entorno para comprender por ti mismo lo que está pasando. Aunque sólo se trata de ejemplos sencillos, un ingeniero equipado con la Explicación 2 sería más rápido en comprender y resolver el problema subyacente, y todo ello se debe a una observabilidad adecuada.

El seguimiento de los cambios de esquema y del linaje puede darte una visibilidad sin precedentes de la salud y los patrones de uso de tus datos, proporcionando información contextual vital sobre quién, qué, dónde, por qué y cómo se utilizaron tus datos. De hecho, el esquema y el linaje son los dos pilares más importantes de la observabilidad de los datos cuando se trata de comprender las implicaciones posteriores (y a menudo reales) del tiempo de inactividad de los datos.

Ampliar la detección de anomalías con Python y aprendizaje automático

A alto nivel, el aprendizaje automático es fundamental para la observabilidad y el monitoreo de datos a escala. Los detectores equipados con aprendizaje automático pueden aplicarse con más flexibilidad a un mayor número de tablas, eliminando la necesidad de comprobaciones y reglas manuales a medida que crece tu almacén o lago de datos. Además, los detectores con aprendizaje automático pueden aprender y adaptarse a los datos en tiempo real y pueden captar patrones estacionales complicados que, de otro modo, serían invisibles a los ojos humanos. Vamos a sumergirnos: no hace falta experiencia previa en aprendizaje automático.

Como recordarás de las dos secciones anteriores de este ejercicio, volvemos a trabajar con datos astronómicos simulados sobre exoplanetas habitables. Ahora, vamos a limitar de nuevo nuestra atención a la tabla EXOPLANETS, como hicimos anteriormente en el capítulo, para comprender mejor cómo escalar la detección de anomalías con aprendizaje automático, representada en el Ejemplo 4-33.

Ejemplo 4-33. Nuestro fiable conjunto de datos EXOPLANETS

$ sqlite3 EXOPLANETS.db
sqlite> PRAGMA TABLE_INFO(EXOPLANETS);
_id             | TEXT | 0 | | 0
distance        | REAL | 0 | | 0
g               | REAL | 0 | | 0
orbital_period  | REAL | 0 | | 0
avg_temp        | REAL | 0 | | 0
date_added      | TEXT | 0 | | 0

Observa que EXOPLANETS está configurado para realizar un seguimiento manual de un importante metadato -la columna date_added - que registra la fecha en que nuestro sistema descubrió el planeta y lo añadió automáticamente a nuestras bases de datos. Para detectar anomalías de frescura y distribución, utilizamos una sencilla consulta SQL para visualizar el número de entradas nuevas añadidas al día, como se muestra en el Ejemplo 4-34.

Ejemplo 4-34. Consulta para obtener el número de nuevas entradas de EXOPLANETS añadidas al día

SELECT
 DATE_ADDED,
 COUNT(*) AS ROWS_ADDED
FROM
 EXOPLANETS
GROUP BY
 DATE_ADDED;

Esta consulta arroja un conjunto de datos aparentemente sanos, como se muestra en el Ejemplo 4-35. Pero, ¿hay algo más que debamos saber?

Ejemplo 4-35. Resultados del Ejemplo 4-34 (que parecen totalmente estándar)

date_added,ROWS_ADDED
2020-01-01,84
2020-01-02,92
2020-01-03,101
2020-01-04,102
2020-01-05,100
...,...
2020-07-14,104
2020-07-15,110
2020-07-16,103
2020-07-17,89
2020-07-18,104

Estos resultados se visualizan en la Figura 4-15.

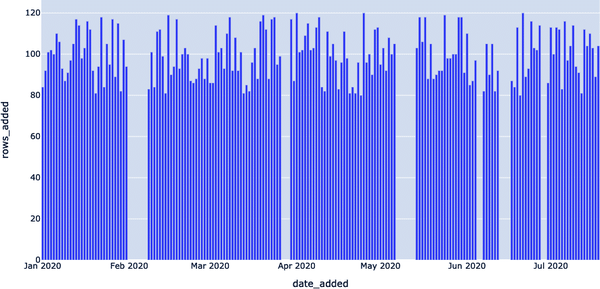
Figura 4-15. Visualización del número de filas añadidas al día en un mes determinado

En otras palabras, la tabla EXOPLANETS se actualiza rutinariamente con unas 100 entradas al día, pero se queda "desconectada" algunos días en los que no se introducen datos, como se muestra en la Figura 4-15. Hemos introducido una métrica llamada DAYS_SINCE_LAST_UPDATE para rastrear este aspecto de la tabla mediante nuestra plantilla de consulta de detección de anomalías, como se muestra en el Ejemplo 4-36. Esto nos dirá cuántos días han pasado desde que se actualizó el conjunto de datos EXOPLANETS, entre entradas distintas.

Ejemplo 4-36. Consulta cuántos días hace que se actualizó el conjunto de datos EXOPLANETS

WITH UPDATES AS(
  SELECT
    DATE_ADDED,
    COUNT(*) AS ROWS_ADDED
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
)
  
SELECT
  DATE_ADDED,
  JULIANDAY(DATE_ADDED) - JULIANDAY(LAG(DATE_ADDED) OVER(
    ORDER BY DATE_ADDED
  )) AS DAYS_SINCE_LAST_UPDATE
FROM
  UPDATES;

Los resultados se listan en un archivo CSV, representado en el Ejemplo 4-37, y se visualizan en la Figura 4-16. Vemos una lista de fechas con nuevas entradas de datos.

Ejemplo 4-37. Resultados del Ejemplo 4-36

DATE_ADDED,DAYS_SINCE_LAST_UPDATE
2020–01–01,
2020–01–02,1
2020–01–03,1
2020–01–04,1
2020–01–05,1
...,...
2020–07–14,1
2020–07–15,1
2020–07–16,1
2020–07–17,1
2020–07–18,1

En la Figura 4-16, podemos ver claramente que hubo algunas fechas de febrero, abril, mayo, junio y julio de 2020 en las que no se añadieron datos a nuestro conjunto de datos EXOPLANETS, lo que indica una anomalía.

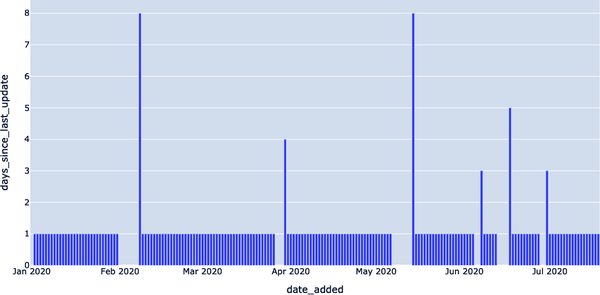
Figura 4-16. Utilizando una consulta de detección de anomalías de frescura, podemos identificar cuándo los datos se "desconectan"

Con una pequeña modificación, introdujimos un parámetro de umbral en nuestra consulta para crear un detector de frescura, que nos permite afinar aún más nuestra detección de anomalías. Nuestro detector devuelve todas las fechas en las que los datos más recientes de EXOPLANETS tenían más de un día, como se muestra en el Ejemplo 4-38.

Ejemplo 4-38. Consulta para identificar cuándo una columna de nuestro conjunto de datos EXOPLANETS no se ha actualizado en más de un día

WITH UPDATES AS(
  SELECT
    DATE_ADDED,
    COUNT(*) AS ROWS_ADDED
  FROM
    EXOPLANETS
  GROUP BY
    DATE_ADDED
),
  
NUM_DAYS_UPDATES AS (
  SELECT
    DATE_ADDED,
    JULIANDAY(DATE_ADDED) - JULIANDAY(LAG(DATE_ADDED)
      OVER(
        ORDER BY DATE_ADDED
      )
    ) AS DAYS_SINCE_LAST_UPDATE
  FROM
    UPDATES
)
  
SELECT
  *
FROM
  NUM_DAYS_UPDATES
WHERE
  DAYS_SINCE_LAST_UPDATE > 1;

El archivo CSV generado por esta consulta se muestra en el Ejemplo 4-39, destacando las anomalías de frescura.

Ejemplo 4-39. Resultados de la consulta del Ejemplo 4-38

DATE_ADDED,DAYS_SINCE_LAST_UPDATE
2020–02–08,8
2020–03–30,4
2020–05–14,8
2020–06–07,3
2020–06–17,5
2020–06–30,3

En la Figura 4-17, podemos visualizar claramente las fechas concretas en las que nuestro conjunto de datos recogía datos obsoletos, probablemente procedentes de un orbitador exoplaneta u otra sonda espacial.

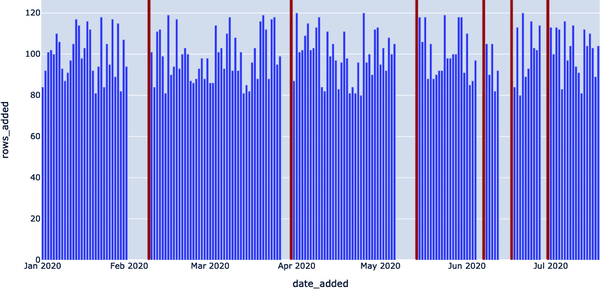
Figura 4-17. Visualización de las fechas en las que la tabla recogía datos "obsoletos", lo que indica un tiempo de inactividad de los datos

Los picos de la Figura 4-17 representan casos en los que la tabla EXOPLANETS estaba trabajando con datos antiguos o "rancios". En algunos casos, estas interrupciones pueden deberse a un procedimiento operativo estándar: quizá nuestro telescopio tenía que estar en mantenimiento, por lo que no se registraron datos durante un fin de semana. En otros casos, sin embargo, una interrupción puede representar un verdadero problema con la recopilación o transformación de los datos: tal vez hemos cambiado las fechas al formato ISO, y el trabajo que tradicionalmente enviaba nuevos datos ahora falla. Puede que tengamos la heurística de que las interrupciones más largas son peores, pero aparte de eso, ¿cómo garantizamos que sólo detectamos los problemas genuinos en nuestros datos?

La respuesta corta: no puedes. Construir un predictor perfecto es imposible (para cualquier problema de predicción interesante, al menos). Pero podemos utilizar algunos conceptos del aprendizaje automático para enmarcar el problema de una forma más estructurada y, como resultado, ofrecer observabilidad de los datos y confianza a escala.

Mejorar las alertas de monitoreo de datos con aprendizaje automático

Siempre que alertamos sobre una tubería de datos averiada, tenemos que preguntarnos si la alerta era exacta. ¿Indica la alerta un verdadero problema? Nos pueden preocupar dos escenarios:

• Se emitió una alerta de monitoreo de datos, pero no había ningún problema real. Hemos hecho perder el tiempo al usuario respondiendo a la alerta.

• Había un problema real, pero no se emitió ninguna alerta de monitoreo de datos. Hemos dejado pasar un problema real sin detectarlo.

Estos dos escenarios se describen como falsos positivos (predicción anómala, en realidad OK) y falsos negativos (predicción OK, en realidad anómala), y queremos evitarlos. Emitir un falso positivo es como dar la alarma, pero todo iba bien. Del mismo modo, dar un falso negativo es como dormir en la guardia: algo iba mal, pero no hicimos nada.

Nuestro objetivo es evitar estas circunstancias en la medida de lo posible y centrarnos en maximizar los verdaderos positivos (predicho anómalo, en realidad un problema) y los verdaderos negativos (predicho OK, en realidad OK).

Contabilización de falsos positivos y falsos negativos

La detección de anomalías es una tarea no supervisada. El aprendizaje no supervisado es una tarea de aprendizaje automático en la que no se conoce el comportamiento óptimo en el momento del entrenamiento. En otras palabras, los datos sobre los que estás entrenando no vienen con etiquetas adjuntas. Por esta razón, puede que te veas obligado a llamar no supervisada a la detección de anomalías, ya que las anomalías no vienen con una verdad de base. Sin una verdad básica, no puedes obtener una señal de error, es decir, la diferencia entre lo que predijiste y lo que deberías haber predicho.

Aunque algunas tareas de detección de anomalías se entienden mejor como problemas de aprendizaje no supervisado, sigue teniendo sentido considerar el vocabulario de señales de error supervisado como falso negativo, falso positivo, precisión, etc. De lo contrario, no podemos comparar diferentes algoritmos de detección entre sí ni tener ninguna métrica para la mejora y el éxito.

Para cualquier punto de datos, un detector de anomalías emite una predicción "anómala" o "no anómala". Además, considera que hay algo de verdad en el asunto: el punto de datos en cuestión o es un verdadero problema, o no lo es en absoluto. Considera una medición que refleje que tu tabla analítica clave no se ha actualizado ni una sola vez en los últimos tres días. Si tu tabla debería actualizarse cada hora, ¡se trata de un auténtico problema!

Cuando un punto de datos es problemático y nuestro detector lo califica de "anómalo", lo llamamos verdadero positivo. Cuando un punto de datos está bien y nuestro detector no lo detecta (es decir, emite "no anómalo"), lo llamamos un verdadero negativo. La Tabla 4-1 ilustra este concepto.

Tabla 4-1. Cuatro posibles resultados de la detección de anomalías

		Predicción
		Negativo	Positivo
Actual	Negativo	Verdadero negativo	Falso positivo
	Positivo	Falso negativo	Verdadero positivo

Los falsos negativos son casos en los que el punto de datos era realmente problemático, pero nuestro detector no lo detectó. Una detección falsa negativa es como un perro guardián dormido: tu algoritmo deja pasar un problema sin detectarlo. Los falsos positivos son casos en los que detectamos una anomalía, pero el punto en cuestión no era realmente problemático. Un falso positivo es como un lobo llorón: tu algoritmo emitió un resultado "anómalo", pero el punto de datos subyacente estaba realmente bien. Los falsos positivos y los falsos negativos son realidades incluso para los algoritmos de detección de anomalías mejor entrenados.

Tanto los falsos positivos como los falsos negativos suenan mal. Parece que las mejores técnicas de detección de anomalías deberían evitar ambos. Por desgracia, por razones de simple estadística, no podemos "evitar ambos". De hecho, menos falsos positivos se consiguen a costa de más falsos negativos, y viceversa.

Para entender por qué, pensemos de nuevo en el niño que gritó lobo, ¡a través de la lente de un detector de anomalías! El niño que gritó lobo detecta cada punto de datos como una anomalía. Como resultado, su detección es muy sensible (no es probable que se le escape ningún falso negativo), pero nada específica (susceptible de producir muchos falsos positivos). A los profesionales de los datos no les gustan los detectores de "niño que gritó lobo" porque sus detecciones no son creíbles. Cuando un detector de anomalías detecta un alto índice de falsos positivos, es probable que creas que la alerta no es auténtica.

El perro guardián dormido es otro tipo de detector de anomalías; en realidad, el tipo opuesto. Este detector nunca considera anómalos los puntos de datos. El algoritmo de detección de anomalías resultante es muy específico (no se producirán falsos positivos), pero nada sensible (se producirán muchos falsos negativos). A los profesionales de los datos tampoco les gustan los detectores de perro guardián dormido, porque sus resultados no son fiables. Los detectores demasiado conservadores nunca emitirán detecciones anómalas, lo que significa que fallarán cuando las cosas vayan realmente mal.

Resulta que el truco está en apuntar a algún punto intermedio entre estos dos esquemas de detección.

Mejorar la precisión y la recuperación

Para una determinada colección de datos, una vez que hayas aplicado un algoritmo de detección de anomalías, tendrás una colección de verdaderos positivos (VP), verdaderos negativos (VN), falsos positivos (FP) y falsos negativos (FN). No solemos fijarnos en estas "puntuaciones" por sí solas: hay formas estadísticas comunes de combinarlas en métricas significativas. Nos centramos en la precisión y el recuerdo, métricas de exactitud que cuantifican el rendimiento del detector de anomalías.

Laprecisión se define como la tasa de predicciones correctas realizadas, por tanto:

$\text{Precisión}=\frac{\text{TPs}}{\text{TPs}\text{+}\text{FPs}}$

En otras palabras: de todos los "positivos" (predicciones realizadas), ¿cuántos son correctos?

La recuperación se define como la tasa de anomalías reales detectadas, por lo que:

$\text{Retirada}=\frac{\text{TPs}}{\text{TPs}\text{+}\text{FNs}}$

En otras palabras: de todas las anomalías auténticas, ¿cuántas hemos detectado?

Estos términos son métricas de precisión populares para los sistemas de clasificación, y sus nombres tienen un significado semántico. Un detector con alta precisión es "exacto" en el sentido de que, cuando predice anomalías, acierta la mayoría de las veces. Del mismo modo, un detector con una alta recuperación "recuerda" bien, ya que capta un alto porcentaje de las anomalías reales.

El problema, por supuesto, es que no puedes tener lo mejor de ambos mundos. Fíjate en que hay una compensación explícita entre ambos. ¿Cómo conseguimos la precisión perfecta? Sencillo: alertando para nada -el perro guardián durmiendo de guardia todo el tiempo- nos obligamos a tener una tasa de falsos positivos del 0%. ¿Cuál es el problema? La recuperación será horrible, ya que nuestra tasa de falsos negativos será enorme.

Del mismo modo, ¿cómo conseguimos un recuerdo perfecto? También es sencillo: alertar de todo -gritando lobo en cada oportunidad- forzando una tasa de falsos negativos del 0%. El problema, como era de esperar, es que nuestra tasa de falsos positivos se resentirá, lo que afectará a la precisión.

Nuestro mundo de datos se rige por objetivos cuantificables, y en la mayoría de los casos querremos optimizar un único objetivo, no dos. Podemos combinar la precisión y la recuperación en una única métrica llamada puntuación F. La fórmula general para β real no negativo es

${\text{F}}_{\beta }=\frac{(1+{\beta }^2)-(\text{Precisión}-\text{Retirada})}{({\beta }^2-\text{Precisión}+\text{Retirada})}$

_Fβ se denomina puntuación F ponderada, ya que los distintos valores de beta ponderan de forma diferente la precisión y la recuperación en el cálculo. En general, una puntuación _Fβ dice: "Considero que la recuperación es beta veces más importante que la precisión".

Cuando β = 1, la ecuación valora a cada uno por igual. Establece β > 1, y la recuperación será más importante para obtener una puntuación más alta. En otras palabras, β > 1 dice: "Me importa más detectar todas las anomalías que causar ocasionalmente una falsa alarma". Del mismo modo, establece β < 1, y la precisión será más importante. β < 1 dice: "Me importa más que mis alarmas sean auténticas que captar todas las anomalías reales".

Hay muchos marcos que puedes utilizar para aplicar la detección de anomalías a escala sin tener que codificar a mano tus algoritmos en Python. Consulta a continuación algunos de nuestros favoritos:

Facebook Profeta

Un modelo de previsión construido para manejar estacionalidades diarias, semanales, mensuales y anuales en datos de series temporales a escala. Los usuarios pueden cargar modelos Profeta de referencia y ajustar los parámetros del modelo interpretables por humanos, añadiendo conocimientos del dominio mediante el aumento de las características. El paquete está disponible tanto en Python como en R.

TensorFlow

Una popular biblioteca de aprendizaje automático para diversas tareas, como el procesamiento del lenguaje natural, la visión por ordenador y la detección de anomalías en series temporales. El paquete proporciona implementaciones útiles y bien documentadas de algoritmos de detección de anomalías más avanzados. El paquete Keras de TensorFlow, por ejemplo, implementa un modelo autoencoder que puede utilizarse para una forma neuronal de autoregresión, más potente que un modelo básico autoregresivo-integrado-de-media móvil (ARIMA).

PyTorch

Desarrollada en Facebook, es otra biblioteca Python de aprendizaje automático que cumple casos de uso similares a TensorFlow (desarrollado por Google). PyTorch suele tener mayor aceptación en el sector académico, mientras que TensorFlow goza de mayor popularidad en el sector industrial.

scikit-learn

Otro popular paquete de software de aprendizaje automático con implementaciones para todo tipo de algoritmos. Además de métodos de detección de anomalías en series temporales como ARIMA, scikit-learn tiene versiones del algoritmo k-próximo más cercano y del algoritmo del bosque de aislamiento, dos métodos populares para la agrupación. Al igual que TensorFlow, scikit-learn está desarrollado en Python.

MLflow

Una popular herramienta de seguimiento de experimentos desarrollada como código abierto por los creadores de Databricks. El seguimiento de experimentos se refiere al proceso de gestión de modelos de aprendizaje automático en desarrollo y producción. MLflow es principalmente un software de seguimiento y reproducción de experimentos. Las instancias de MLflow tienen registros de modelos compartidos donde se pueden hacer copias de seguridad de los experimentos y compararlos entre sí. Cada modelo pertenece a un proyecto, que es un entorno de software empaquetado diseñado para garantizar la reproducibilidad del modelo, como se muestra en la Figura 4-18. Un aspecto importante del desarrollo de software de detección de anomalías es la garantía de que el código se ejecuta igual en diferentes máquinas. No querrás pensar que has resuelto un fallo localmente sólo para que la corrección no se aplique en producción. Del mismo modo, si un colega informa de una métrica de precisión para su modelo actualizado, te gustaría saber que puedes replicar tú mismo sus resultados de calidad. También con proyectos, el registro MLflow ayuda a la implementación de modelos en entornos de producción, incluidos Azure ML y Amazon SageMaker, o en clústeres Spark como Apache Spark UDF.

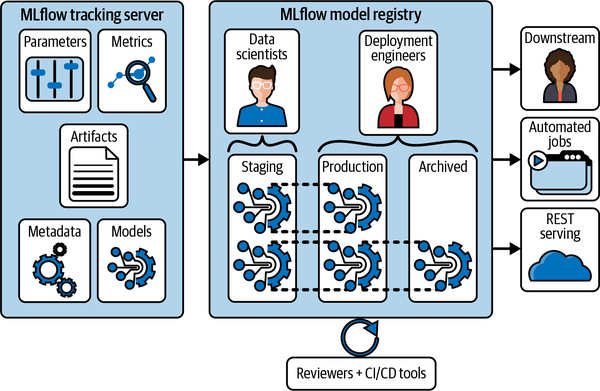
Figura 4-18. Registro de modelos de MLflow visualizado en el flujo de trabajo de ciencia de datos

Nota

Elseguimiento de experimentos, el proceso de gestionar el desarrollo y entrenamiento de modelos de aprendizaje automático, implica la comparación de hiperparámetros, la comprobación de dependencias, la gestión y orquestación de trabajos de entrenamiento, el almacenamiento de instantáneas de modelos y la recopilación de registros, ¡entre otras tareas! En principio, esto puede hacerse utilizando algunas hojas de cálculo increíblemente complicadas, aunque obviamente hay mejores herramientas para el trabajo.

TensorBoard

Se trata del conjunto de herramientas de visualización de TensorFlow, aunque no necesitas modelar con TensorFlow para aprovechar el software. Con TensorBoard, como se muestra en la Figura 4-19, puedes visualizar métricas comunes de aprendizaje automático como la pérdida por época de entrenamiento, matrices de confusión y análisis de errores individuales.

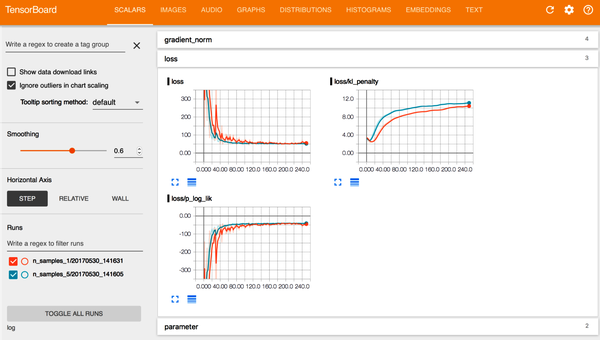
Figura 4-19. Una vista estándar del TensorBoard durante el entrenamiento del modelo. Fuente: Tran et al.¹

Estos y otros marcos pueden llevar tus detectores de anomalías al siguiente nivel, eliminando los falsos negativos y positivos y reduciendo la necesidad de ajustar el modelo a lo largo del tiempo.

Detectar incidentes de frescura con el monitoreo de datos

Con nuestro nuevo vocabulario en la mano, volvamos a la tarea de detectar incidencias de frescura en la tabla EXOPLANETS. Estamos utilizando un algoritmo de predicción simple, ya que convertimos nuestra consulta en un detector estableciendo un parámetro del modelo X. Nuestro algoritmo dice: "Cualquier interrupción superior a X días es una anomalía, y emitiremos una alerta por ella". Incluso en un caso tan sencillo como éste, ¡la precisión, el recuerdo y las puntuaciones F pueden ayudarnos!

Para demostrarlo, tomamos los cortes de frescura en EXOPLANETS y asignamos etiquetas de verdad básica que codifican si cada corte es un incidente genuino o no. Es imposible calcular la precisión de un modelo sin algún tipo de verdad sobre el terreno, por lo que siempre es útil pensar en cómo generarlas para tu caso de uso. Recuerda que hay un total de seis interrupciones que duran más de un día en la tabla EXOPLANETS, como se destaca en los datos representados en el Ejemplo 4-40.

Ejemplo 4-40. Resultados de la consulta del Ejemplo 4-38 sobre interrupciones de más de un día de duración

DATE_ADDED,DAYS_SINCE_LAST_UPDATE
2020–02–08,8
2020–03–30,4
2020–05–14,8
2020–06–07,3
2020–06–17,5
2020–06–30,3

Digamos, arbitrariamente, que los incidentes de 2020-02-08 y 2020-05-14 son auténticos. Cada una dura ocho días, por lo que tiene sentido que sean problemáticas. Por otro lado, supongamos que las interrupciones de 2020-03-30 y 2020-06-07 no son incidentes reales. Estas interrupciones duran cuatro y tres días, respectivamente, así que no es descabellado. Por último, supongamos que las interrupciones de 2020-06-17 y 2020-06-30, de cinco y tres días, respectivamente, también son incidentes reales, como se muestra en el Ejemplo 4-41.

Ejemplo 4-41. Clasificación de las anomalías "verdaderas

INCIDENT,NOT INCIDENT
2020-02-08 (8 days),2020-03-30 (4 days)
2020-05-14 (8 days),2020-06-07 (3 days)
2020-06-17 (5 days),
2020-06-30 (3 days),

Habiendo elegido nuestra verdad de base de este modo, vemos que es más probable que las interrupciones más largas sean problemas reales, pero no hay ninguna garantía. Esta débil correlación hará que un buen modelo sea eficaz, pero imperfecto, igual que lo sería en casos de uso reales más complejos. Para mejorar la precisión del modelo, no tenemos más remedio que recurrir a una de las herramientas más comunes de un ingeniero de datos o de ML: la puntuación F.

Puntuación F

Las puntuaciones F son métricas de precisión de clasificación diseñadas para optimizar conjuntamente la precisión y la recuperación. La "predeterminada" es_{la puntuación F1}, definida (para los estadísticos) como la media armónica entre la precisión y la recuperación:

${\text{F}}_1=\frac{2}{\frac{1}{\text{Precisión}}+\frac{1}{\text{Retirada}}}$

Esto significa que la_{puntuación F1} está diseñada para equilibrar a partes iguales la precisión y la recuperación, lo que significa que recompensamos las ganancias en una tanto como en la otra. En algunos contextos, este tipo de evaluación puede ser apropiado. Sin embargo, en otros casos, el recuerdo o la precisión pueden ser mucho más importantes.

Un ejemplo del mundo real que pone de manifiesto este punto: el sábado 13 de enero de 2018 por la mañana, los habitantes de las islas hawaianas recibieron mensajes de texto informándoles de que se aproximaba un misil balístico y que debían buscar refugio subterráneo inmediatamente. La alerta se emitió a las 8:07 a.m. y terminaba ominosamente con "Esto no es un simulacro".

Treinta y ocho minutos más tarde, después de que la red telefónica hawaiana y la línea de emergencia 911 dejaran de funcionar por sobrecarga, el gobierno del estado de Hawai comunicó que la alerta había sido un error. Aunque un hawaiano sufrió un infarto al oír la noticia, no hubo víctimas mortales inmediatas del suceso.

El incidente hawaiano se había concebido como una prueba del sistema de alerta real de la isla; el problema fue, en cambio, que el sistema había enviado una alerta real por error. En este caso, la alerta real es un ejemplo de detección de anomalías que ha salido mal, en el mundo real: un falso positivo. Ahora bien, aunque ciertamente asusta, considera el falso negativo equivalente y las posibles repercusiones que tendría. Al considerar las repercusiones en el mundo real, las consecuencias cuando las cosas no funcionan como se esperaba podrían ser graves.

¿Qué significa esto para el diseño de productos y qué podemos hacer para mitigarlo? En términos de lo que hemos estado debatiendo aquí: un falso positivo es mejor que un falso negativo para el sistema de detección de misiles. Es decir: el recuerdo es más importante que la precisión. Si estamos examinando el rendimiento de un sistema como éste, deberíamos utilizar algo distinto de la_{puntuación F1}. En concreto, una puntuación _Fβ general nos permite decir: "la recuperación es beta veces más importante que la precisión para mi detector":

${\text{F}}_{\beta }=\frac{1+{\beta }^2}{\frac{{\beta }^2}{\text{Precisión}}+\frac{1}{\text{Retirada}}}$

Cuando β = 1, observa que esta ecuación resulta igual que la ecuación_{de la puntuación F1}. También diría "la recuperación es una vez más importante que la precisión", ponderándolas por igual. Sin embargo, si estuviéramos probando algo como un sistema de alerta de misiles en el que el recuerdo fuera dos o tres veces más importante, podríamos considerar la posibilidad de evaluar utilizando una _F2 o una _F3.

¿Importa la precisión del modelo?

En las últimas páginas, habrás notado que utilizamos poco la palabra "precisión". Se supone que los algoritmos de aprendizaje automático, incluidos los detectores de anomalías, son "precisos", o eso has oído. ¿Por qué no utilizamos entonces ese vocabulario?

He aquí parte de nuestra respuesta (un ejemplo extraído de un profesor de Stanford, Mehran Sahami). Supongamos que estás construyendo un sofisticado sistema de detección de anomalías mediante aprendizaje automático para detectar el síndrome de inmunodeficiencia adquirida (SIDA). Así es como funciona nuestro sofisticadísimo sistema: simplemente predice "No" cada vez que le preguntas si alguien tiene SIDA. En la actualidad, el SIDA afecta aproximadamente a 1,2 millones de personas en Estados Unidos. La población estadounidense ronda los 330 millones de habitantes. Nuestra "precisión", o lo acertados que estamos de media, es 1 - (estadounidenses con SIDA / estadounidenses) = 1 - (1,2 millones / 330 millones) = 99,6%. Es una de las mejores precisiones que hemos visto nunca; sin duda, digna de publicación, motivo de celebración, etc.

Espero que este ejemplo ilustre la cuestión: la precisión no es tan simple como lo correcto que sea tu detector por término medio, y además no debe definirse igual para diferentes aplicaciones. Al fin y al cabo, el resultado de basarse en las métricas de precisión del ejemplo anterior sería diagnosticar erróneamente a decenas de miles de individuos, o más. A fin de cuentas, queremos que un buen esquema de detección minimice tanto los falsos positivos como los falsos negativos. En la práctica del aprendizaje automático, es más habitual pensar en términos relacionados pero más perspicaces, precisión y recuerdo, como se muestra en la Figura 4-20.

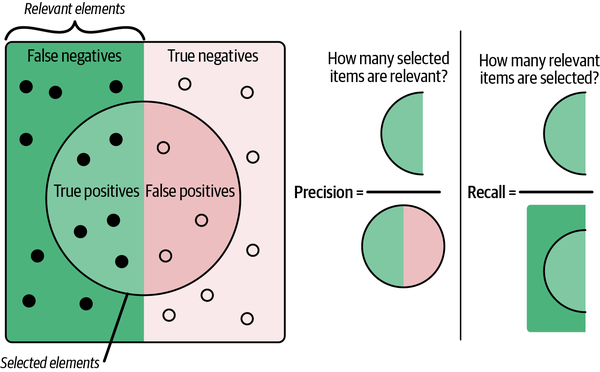
Figura 4-20. Precisión (frecuencia con la que tu algoritmo detecta una anomalía) y recuperación (número de anomalías detectadas)

Como se ha dicho antes en el capítulo, la precisión, en general, nos dice con qué frecuencia acertamos cuando emitimos una alerta. Los modelos con buena precisión emiten alertas creíbles, ya que su alta precisión garantiza que den la voz de alarma con muy poca frecuencia.

La llamada a revisión, en general, nos dice de cuántos problemas alertamos realmente. Los modelos con una buena recuperación son fiables, ya que su alta recuperación garantiza que rara vez se duermen en el trabajo.

Ampliando nuestra metáfora, un modelo con buena precisión es un modelo que rara vez da voces de alarma: cuando emite una alerta, más vale que te lo creas. Del mismo modo, un modelo con buena capacidad de recuperación es como un buen perro guardián: puedes estar seguro de que este modelo detectará todos los problemas auténticos.

Ahora, supongamos que empezamos fijando nuestro umbral en tres días, es decir, "cada interrupción superior a tres días es una anomalía". Esto significa que detectamos correctamente anomalías en 2020-02-08, 2020-05-14 y 2020-06-17, por lo que tenemos tres verdaderos positivos. Pero, por desgracia, detectamos el 2020-03-30 como una incidencia cuando no lo es, por lo que tenemos un falso positivo. Tres verdaderos positivos / (tres verdaderos positivos + un falso positivo) significa que nuestra precisión es de 0,75. Además, no detectamos el 2020-06-30 como incidente, lo que significa que tenemos un falso negativo. Tres verdaderos positivos / (tres verdaderos positivos + un falso negativo) significa que nuestra recuperación también es de 0,75._{Puntuación F1}, dada por la fórmula:

$\frac{\text{TP}}{\text{TP}\text{+}\frac{1}{2}\left(\text{FP}\text{+}\text{FN}\right)}$

Introduciendo los valores adecuados, esto significa que nuestra_{puntuación F1} también es 0,75. ¡No está mal!

Supongamos que fijamos el umbral más alto, en 5 días. Ahora sólo detectamos 2020-02-08 y 2020-05-14, las interrupciones más largas. Ambos resultan ser incidentes auténticos, por lo que no tenemos falsos positivos, ¡lo que significa que nuestra precisión es de 1 perfecto! Pero observa que no detectamos otras anomalías auténticas, 2020-06-17 y 2020-06-30, lo que significa que tenemos dos falsos negativos. Dos verdaderos positivos / (dos verdaderos positivos + dos falsos negativos) significa que nuestro recuerdo es 0,5, peor que antes. Es lógico que nuestra recuperación se haya resentido, porque hemos elegido un clasificador más conservador con un umbral más alto. Nuestra_{puntuación F1} puede calcularse de nuevo con la fórmula anterior, y resulta ser 0,667.

Si trazamos nuestra precisión, recuperación y_{puntuación F1} en función del umbral que establezcamos, observamos algunos patrones importantes. En primer lugar, los detectores agresivos con umbrales bajos tienen la mejor recuperación, ya que son más rápidos en alertar y, por tanto, detectan más problemas reales. Por otro lado, los detectores más pasivos tienen mejor precisión, ya que sólo alertan de las peores anomalías que tienen más probabilidades de ser auténticas. La_{puntuación F1} alcanza su punto máximo en algún punto entre estos dos extremos, en este caso, en un umbral de cuatro días. Encontrar el punto óptimo es clave para ajustar mejor nuestros detectores, como se muestra en la Figura 4-21.

Por último, veamos una última comparación(Figura 4-22). Observa que sólo hemos tenido en cuenta_{la puntuación F1}, que pondera por igual la precisión y la recuperación. ¿Qué ocurre si consideramos otros valores de beta?

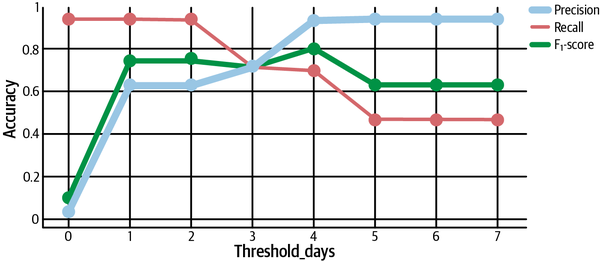
Figura 4-21. Calcular la precisión, la recuperación y_{la puntuación F1} y trazar los resultados para determinar cómo ajustar los detectores de anomalías

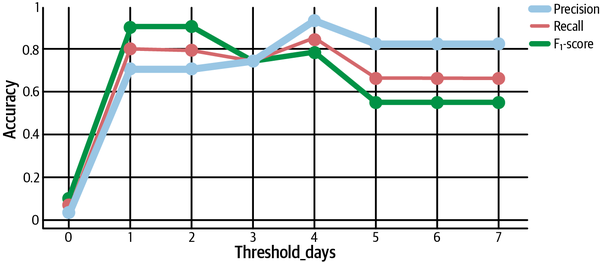
Figura 4-22. Cálculo de la puntuación F con distintos valores de β

Recordemos que un _Fβ general dice "recall es β veces más importante que la precisión". Por tanto, deberíamos esperar que _F2 sea mayor que_F1 cuando se prioriza el recuerdo, que es exactamente lo que vemos con umbrales inferiores a 4, como se muestra en la Figura 4-22. Al mismo tiempo, la_puntuación F0_,5 es más alta para umbrales mayores, lo que muestra una mayor permisividad para los clasificadores conservadores con mayor precisión.

Con esta puntuación F y un algoritmo mejor afinado, estarás preparado para detectar problemas en los cinco pilares de la observabilidad de los datos: frescura, volumen, distribución, esquema y linaje.

Más allá de la superficie: Otros Enfoques Útiles para la Detección de Anomalías

Los mejores algoritmos de detección de anomalías hacen tres cosas: detectar problemas casi en tiempo real, alertar a los que tienen que saberlo y darte información que te ayude a evitar que se produzcan tiempos de inactividad en el futuro. En este capítulo hemos recorrido los enfoques habituales y los elementos clave de los algoritmos básicos de detección de anomalías, pero nuestro ejemplo sólo araña la superficie. Hay otras buenas prácticas, componentes de algoritmos y metodologías que garantizan resultados similares, o incluso más precisos, dependiendo de las herramientas que utilices:

Definiciones de reglas o umbrales duros

Las definiciones de las reglas establecen límites explícitos para determinados valores métricos y determinan las anomalías en relación con el umbral. Aunque técnicamente es detección, este enfoque sólo puede llamarse propiamente detección de "anomalías" si la mayoría de los puntos de datos se encuentran dentro del umbral. Las definiciones de reglas son increíblemente escalables y podrían funcionar para SLA extremadamente bien definidos, garantías de tiempo de actividad de los datos, etc.

Modelos autorregresivos

La Autorregresión funciona en la detección de anomalías en series temporales, donde los puntos de datos se ordenan mediante un objeto de marca de tiempo. Los modelos autorregresivos toman datos de pasos temporales anteriores, los introducen en un modelo de regresión (lineal) y utilizan el resultado para formar una predicción de dónde estarán los datos de la siguiente marca temporal. Los puntos de datos que se alejan demasiado de la predicción autorregresiva se marcan como anómalos. Combinada con un algoritmo simple de media móvil, la autorregresión nos da los algoritmos de detección de media móvil autorregresiva y ARIMA. Si hubiéramos llevado nuestro ejemplo del exoplaneta un paso más allá y hubiéramos añadido la autorregresión, este conjunto de datos habría funcionado bastante bien.

Alisamiento exponencial

Existen métodos de alisamiento exponencial para eliminar la tendencia y la estacionalidad de las series temporales, de modo que enfoques más ingenuos (por ejemplo, ARIMA) puedan tomar el relevo. Holt-Winters es un famoso modelo estacional para la previsión de series temporales, y existe, de nuevo, una rica taxonomía (aditivo, multiplicativo, amortiguado, no amortiguado, etc.).

Agrupación

Las técnicas de agrupación, como el algoritmo del vecinomás próximo k o el algoritmo del bosque de aislamiento, encuentran anomalías colocando puntos de datos similares en cubos, y alertándote de los "raros", es decir, de los datos que encajan en cubos pequeños o incluso únicos.

Ajuste de hiperparámetros

Los modelos de aprendizaje automático tienen muchos parámetros, que son representaciones numéricas de los datos utilizados por el algoritmo de predicción. Algunos parámetros se aprenden utilizando los datos y el proceso de entrenamiento. Por ejemplo, con un modelo de puntuación z, μ y σ son parámetros establecidos automáticamente a partir de la distribución de los datos de entrada. Otros parámetros, llamados hiperparámetros, no se establecen mediante el proceso de aprendizaje, sino que dictan los procesos de aprendizaje e inferencia de determinadas maneras. Algunos hiperparámetros afectan a la arquitectura del modelo, por ejemplo, el tamaño de una red neuronal, el tamaño de las matrices de incrustación y de estado oculto, etc. Se denominan hiperparámetros del modelo. Otra clase, los hiperparámetros del algoritmo, afectan a la forma en que se realiza el entrenamiento, por ejemplo la tasa de aprendizaje, el número de épocas o el número de puntos de datos por lote de entrenamiento.

Marco del modelo conjunto

Un marco de modelo conjunto toma lo mejor de cada método -un poco de agrupación, suavizado exponencial y nodos autorregresivos combinados en una red neuronal de avance- ycombina sus predicciones mediante un algoritmo conjunto de votación mayoritaria.

Aunque son importantes, estos enfoques quedan fuera del alcance de este libro: para saber más sobre cómo crear grandes algoritmos de detección de anomalías, te sugerimos que consultes Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow (O'Reilly), de Aurélien Géron.

Diseño de monitores de calidad de datos para almacenes frente a lagos

A la hora de crear monitores de calidad de datos para tu sistema de datos, es importante distinguir si trabajas con datos estructurados y monolíticos de un almacén o si te adentras en el salvaje oeste del ecosistema moderno de los lagos de datos.

Las principales diferencias entre diseñar algoritmos de detección de anomalías para almacenes y lagos se reducen a:

• El número de puntos de entrada que tienes que tener en cuenta

• Cómo se recogen y almacenan los metadatos

• Cómo puedes acceder a esos metadatos

En primer lugar, los sistemas de lago de datos tienden a tener un gran número de puntos de entrada, lo que significa que hay que suponer una gran heterogeneidad en los datos que entran desde distintas fuentes. Al monitorear, por ejemplo, las tasas de nulos en los datos tabulares que entran desde Postgres, los registros de aplicaciones y una API web, un científico de datos podría observar grupos de comportamiento de tablas correspondientes a los diferentes puntos finales. En estos casos, desconfía de un enfoque de modelado de "talla única". Lo más probable es que diferentes arquitecturas de modelos (por ejemplo, diferentes hiperparámetros) funcionen mejor para predecir anomalías en cada formato diferente. Una forma de hacerlo es condicionar el punto final de los datos en sí, formando una nueva característica para introducir en el modelo de aprendizaje automático. Otra es utilizar una arquitectura de modelo de conjunto, o simplemente tener modelos separados para cada uno de tus casos de uso.

En segundo lugar, los metadatos recogidos directamente en un lago de datos pueden necesitar diversos niveles de preprocesamiento antes de que puedas esperar que un algoritmo de detección de anomalías obtenga algo de valor de ellos. Los tipos pueden necesitar coerción, los esquemas pueden necesitar alineación, y puedes encontrarte derivando características aumentadas totalmente nuevas en los datos antes de ejecutar la tarea de entrenamiento del detector.

Está bien hacerlo inmediatamente antes del entrenamiento del modelo, siempre que no estés atascando tus recursos informáticos aplicando "transformaciones" en grandes lotes de datos de entrada. En algunos casos, puede ser ventajoso idear algunos pasos de ELT entre los datos del lago y el algoritmo de aprendizaje automático. En "Limpieza de datos" se explica por qué esto puede ser valioso.

Resumen

En este capítulo, hemos hecho un rápido safari por el monitoreo y la detección de anomalías en relación con las comprobaciones básicas de la calidad de los datos. Ahora, ¿cómo pueden ayudarnos estos conceptos a aplicar los detectores a nuestros entornos de producción en almacenes y lagos de datos?

La clave está en comprender que no existe un clasificador perfecto para ningún problema de detección de anomalías. Siempre hay un equilibrio entre falsos positivos y falsos negativos, o lo que es lo mismo, entre precisión y recuperación. Tienes que preguntarte: "¿Cómo sopeso la compensación entre ambos? ¿Qué determina el "punto óptimo" para los parámetros de mi modelo?". Elegir una puntuación _Fβ para optimizar decidirá implícitamente cómo sopesas estos sucesos, y por tanto qué es lo que más importa en tu problema de clasificación.

Además, recuerda que cualquier debate sobre la precisión de un modelo no está completo sin algún tipo de verdad de base que comparar con las predicciones del modelo. Necesitas saber en qué consiste una buena clasificación antes de saber que tienes una. En el Capítulo 5, hablaremos de cómo aplicar las tecnologías destacadas en los Capítulos 2, 3 y 4 a la arquitectura de sistemas de datos más fiables, así como de nuevos procesos, como los SLA, SLI y SLO, para ayudarles a escalar.

¹ Dustin Tran, Alp Kucukelbir, Adji B. Dieng, Maja Rudolph, Dawen Liang y David M. Blei, "Edward: A Library for Probabilistic Modeling, Inference, and Criticism", arXiv preprint arXiv:1610.09787, 2016, https://oreil.ly/CvuKL.