From Euclidean to Hilbert Spaces

3Lebesgue’s Measure and Integration Theory

In this chapter, we shall present the most essential elements of measure theory and integration. Our aim here is simply to establish clear and unambiguous notation and a common vocabulary.

What follows is a deliberately brief summary. Readers who have not yet studied this important branch of mathematics may wish to look elsewhere for a more detailed introduction to measure theory and integration.

Two excellent reference works in this domain are Briane and Pagès (1998) and Bartle (1966).

3.1. Riemann versus Lebesgue

The main difference between the Riemann and Lebesgue approaches is shown in Figure 3.1.

The key to Riemann integration lies in approximating the area of the surface between the x axis and the curve of a function f using small rectangles [a_i−1, a_i] × [0, Φ_i] with their base on the x axis, of a height Φ_i close to the average height of function f over [a_i−1, a_i].

Lebesgue’s integration theory differs in that the first stage involves breaking down the y axis into small intervals [b_j−1, b_j]; the surface below the curve f is then approximated using:

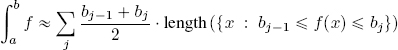
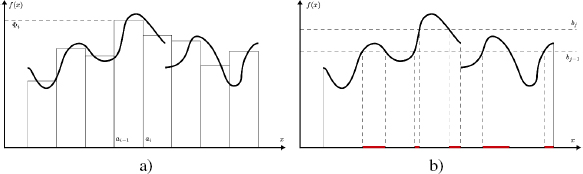
Figure 3.1. Riemann and Lebesgue integration. For a color version of this figure, see www.iste.co.uk/provenzi/spaces.zip

The main difficulty lies in the fact that the sets:

shown ...