Ereignisdiskrete Systeme, 3rd Edition

$\overline{p}=\frac{1}{N}1$

gilt. Notwendig und hinreichend dafür ist die Forderung, dass die Markovkette symmetrisch ist (G = GT), denn genau dann ist $\overline{p}$ aus Gl. (7.50) ein Eigenvektor der Matrix G zum Eigenwert λ{G} =1.

Beispiel 7.11Stationäre Wahrscheinlichkeitsverteilung einer Markovkette

Die in Abb. 7.35 gezeigte Markovkette wird nichtperiodisch, wenn man beispielsweise um den Knoten 2 eine Schlinge einträgt (Abb. 7.36 (links)). Dann existiert eine stationäre Wahrscheinlichkeitsverteilung.

Abb. 7.36: Nichtperiodische Markovkette: Automatengraph (links) und Zustandswahrscheinlichkeitsverteilung (rechts)

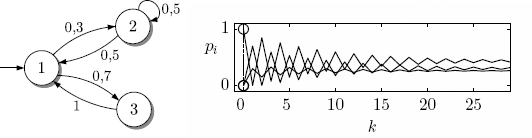
Gleichung (7.48) führt auf den Vektor ...