48 Equivalence and Noninferiority Tests
Discussion:
If
σ= σk
1
2
0
2
2
2
then
−σ
−σ
nSk
nS
(1)
(1)
11
2
0
2
2
2
22
2
2
2
has an F-distribution with n
1
− 1 and n
2
− 1 degrees of freedom in the numer-
ator and denominator, respectively. Thus,
−
−
−−
nS
nS
kF
nn
(1)
(1)
~(1,
1)
11
2
22
2
0
2
12
.
Therefore,
kFnn Fn n
Fn n
k
Fn n
Pr (1,1)(1, 1)
Pr (1,1)
1
(1
,1
)
1
0
2
12 11 2
12
0
2
11 2
{}
−−≤−−
=−−≤
−−
=−β
−β
−β
so
−
−
≤−−
=−β
−β
nS
nSk
Fn nPr
(1)
(1)
1
(1,1
)1
11
2
22
2
0
2
11 2
.
If in fact
kk
k,
aa
1
22
2
2
0
σ=
σ>
then, as
k
a
2
gets larger than
k
0
2
, the power decreases. That is, the power is
givenby:
≤−
−
−β
Pr F
k
k
Fn n(1
,1
a
0
2
2
11 2
.
Example:
Suppose:
k
0
2
= 1.0
49Variances (Standard Deviations) and Coefficients of Variation
S
1
= 5.0
S
2
= 6.0
n
1
= n
2
= 10
and 1 – β = 0.95, so
−
−
=≈
nS
nS
(1)
(1)
9*5.0
9*6.0
0.694
11
2
22
2
2
2
−−≈
−β
k
Fn n
1
(1,1)
3.1789
0
2
11 2
.
Since
−
−
≤−−≈
−β
nS
nSk
Fn n
(1)
(1)
1
(1,1) 3.1789
11
2
22
2
0
2
11 2
we reject H
0
.
The power curve for this example is given as a function of k
a
≥ k
0
= 1.0 in
Figure3.3.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0.75 1 1.25 1.5 1.7522.25 2.5 2.75 3 3.25 3.5 3.75 4
Power
ka
FIGURE 3.3
Test 3.2, power curve for comparison of two variances.
50 Equivalence and Noninferiority Tests
Condence interval formulation:
=
−
−
−−
−β
k
nS
nS
Fn n
ˆ
(1)
(1)
(1
,1
)
U
22
2
11
2
11 2
is an upper 100(1 − β) percent condence limit for
=
σ
σ
k
1
2
.
The example data yield:
k
nS
nS
Fn n
ˆ
(1)
(1)
(1,1)
(101)36
(101)25
(3.1789) 4.578
U
22
2
11
2
11 2
=
−
−
−−=
−
−
≈
−β
.
Note that as n
1
and n
2
get large, F
1−β
(n
1
− 1, n
2
− 1) will get smaller.
Computational considerations:
• SAS code
libname stuff 'H:\Personal Data\Equivalence & Noninferiority\
Programs & Output';
data calc;
set stuff.d20121107_test_3_2_example_data;
run;
proc means data = calc;
var X1 X2 k0;
output out = onemean MEAN = xbar1 xbar2 k0val VAR = v1 v2
N= n1 n2;
run;
data outcalc;
set onemean;
beta = 0.05;
var_ratio = ((n1-1)*v1)/((n2-1)*v2);
crit_val = finv(1-beta,n1-1,n2-1)/k0val**2;
run;
proc print data = outcalc;/* has vars xbar1 xbar2 k0val v1 v2
n1 n2 beta var_ratio crit_val */
run;
51Variances (Standard Deviations) and Coefficients of Variation
The SAS System 13:53 Wednesday, November 7, 2012 7
The MEANS Procedure
Variable Label N Mean Std Dev Minimum Maximum
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
X1 X1 35 0.1920832 1.8406642 -3.8176650 4.3223639
X2 X2 35 0.1100396 2.0376728 -4.5550806 4.7211140
k0 k0 35 1.0500000 0 1.0500000 1.0500000
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
The SAS System 13:53 Wednesday, November 7, 2012 8
var_
Obs _TYPE_ _FREQ_ xbar1 xbar2 k0val v1 v2 n1 n2 beta ratio crit_val
1 0 35 0.192 0.110 1.05 3.38804 4.15211 35 35 0.05 0.81598 1.60732
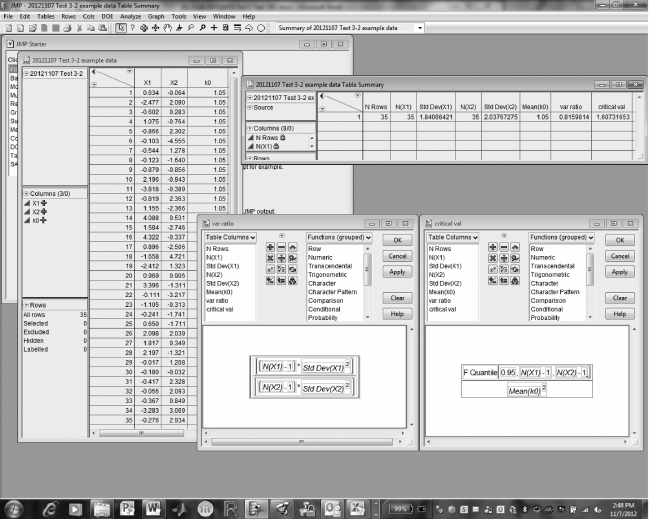
• JMP Data Table and formulas (Figure3.4)
FIGURE 3.4
Test 3.2, JMP screen.
52 Equivalence and Noninferiority Tests
Test 3.3 Single Coefficient of Variation (One-Sided)
Parameters:
=
σ
µ
c
= coefcient of variation (cv)
c
0
= upper tolerable bound on c.
1 – β = power to reject the null if c equals c
0
.
Hypotheses:
H
0
: c > c
0
H
1
: c ≤ c
0
Data:
c
ˆ
ˆ
ˆ
sample
cv
=
σ
µ
= .
n = sample size.
Critical value(s):
Reject H
0
if
≤
′
β−
c
n
Tn
n
c
ˆ
,1;
0
.
′
β−
Tn
n
c
,1;
0
is the 100(β) percentile of a noncentral t-distribution with n – 1 degrees of
freedom and noncentrality parameter
n
c
.
0
Discussion:
The critical value and subsequent power calculations are all based on an
approximation to the distribution of the sample
=
σ
µ
cCV,
ˆ
ˆ
ˆ
.

Get Equivalence and Noninferiority Tests for Quality, Manufacturing and Test Engineers now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial