Engineering Optimization, 5th Edition

Appendix A Convex and Concave Functions

Convex Function

A function f (X) is said to be convex if for any pair of points

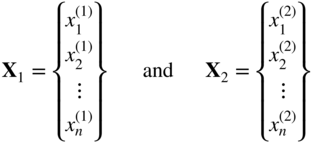
and all λ, 0 ≤ λ ≤ 1,

(A.1)

that is, if the segment joining the two points lies entirely above or on the graph of f (X). Figures A.1a and A.2a illustrate a convex function in one and two dimensions, respectively. It can be seen that a convex function is always bending upward and hence it is apparent that the local minimum of a convex function is also a global minimum.

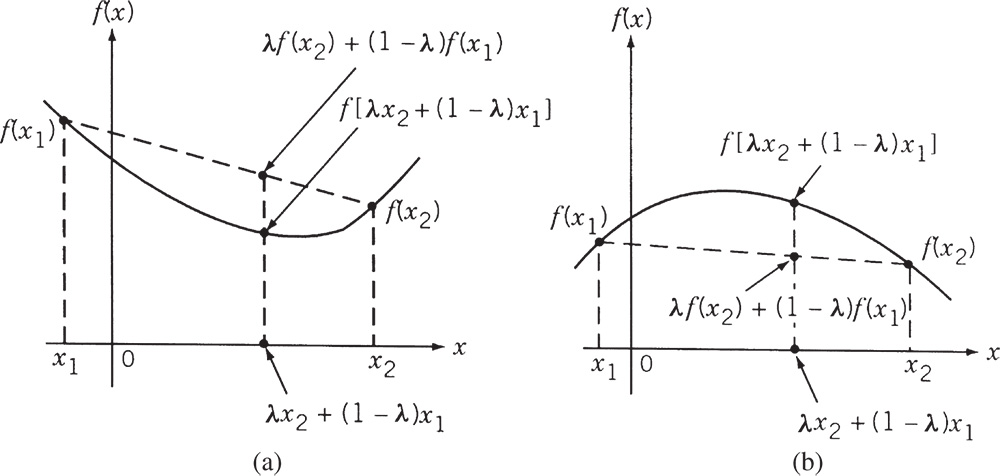
Figure A.1 Functions of one variable: (a) convex function in one variable; (b) concave function in one variable.

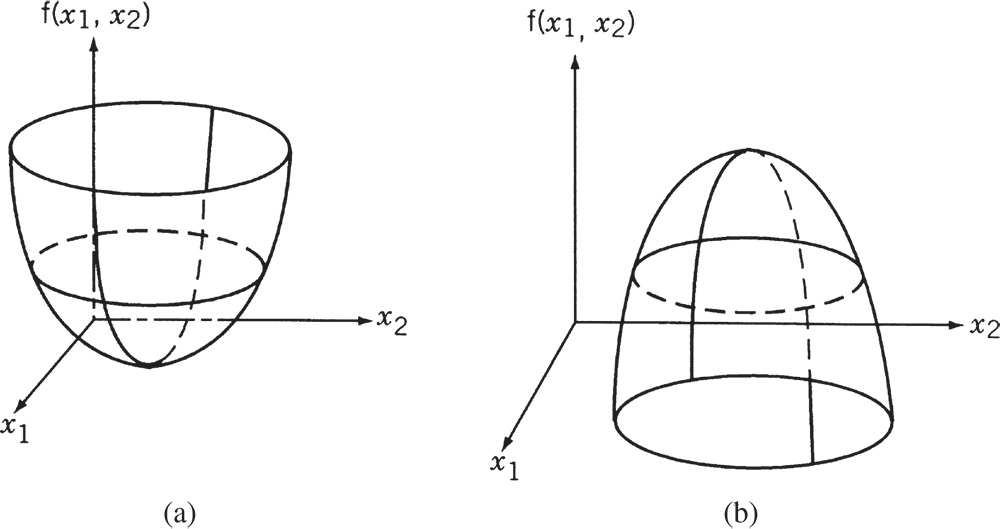
Figure A.2 Functions of two variables: (a) convex function in two variables; (b) concave function in two variables.

Concave Function

A function f (X) is called a concave function if for any two points X ₁ and X ₂, and for all 0 ≤ λ ≤ 1,

(A.2)

that is, if the line segment joining the two points lies entirely below or on the graph of f (X).

Figures ...