Electromagnetism

Appendix 3

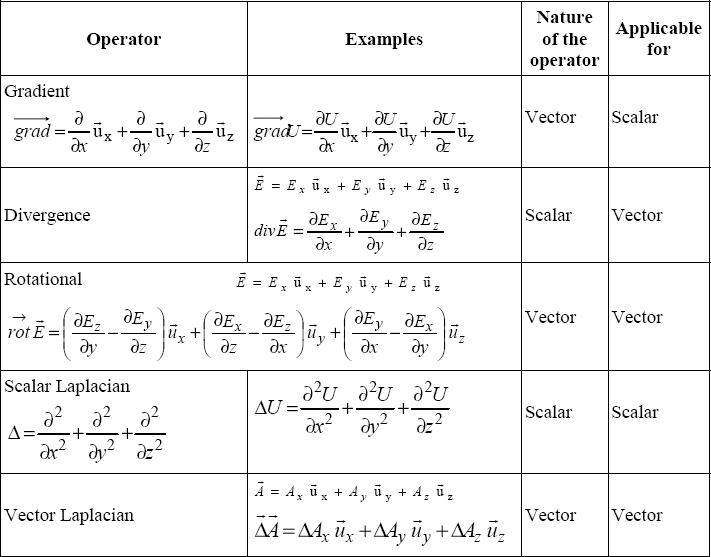
Operator Expressions in Cartesian Coordinates

For a color version of all figures in this book, see www.iste.co.uk/gontrand/electromagnetism.zip.

Cylindrical coordinates

When a property depends only on the distance to an axis (problems with cylindrical symmetry), it may be advantageous to take account of symmetry by making the axis oz play a privileged role. The opposite figure shows a Cartesian coordinate system (O,x,y,z) and a cylindrical coordinate system (0, r, θ, z). A point M in space projects in m on the polar plane and in p on the axis Oz.

The cylindrical coordinates of M are r, θ and z: M(r,θ,z):

r = 0M is the distance from M to the axis: (0 < r < +∝);

θ = < Ox,OM > is the polar angle (0 ≤ θ ≤ 2π);

z is the height(-∝ ≤ φ ≤ +∝).

The frame consists of three vectors:

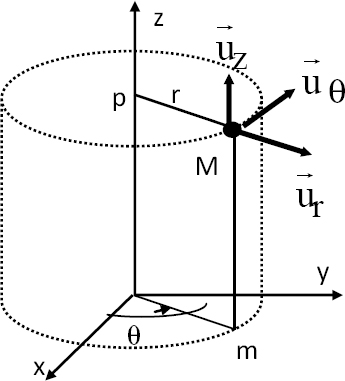
Figure A3.1. Cylindrical coordinates

Spherical coordinates

When a property depends only on the distance to a point (problems with spherical symmetry), it is often convenient to consider this point as the origin O of a spherical coordinate system. Figure A.3.2 shows a Cartesian coordinate system ...