Dimensional Analysis and Similarity in Fluid Mechanics

3Similarity of Flows

3.1. Definition and principle of similarity

Similarity allows us to determine whether two flows are comparable, and if they are, to determine the relationships that make it possible to transpose the numerical results from one to the other.

3.1.1. Geometric similarity

If L₁ and L₂ are the reference lengths representing homologous dimensions of the two domains, then their relationship:

[3.1]

is the geometric scale ratio (or length scale ratio) between the prototype (1) and the model (2).

For two homologous points M₁and M₂, the ratios relative to each of the coordinates are equal to A_L:

[3.2]

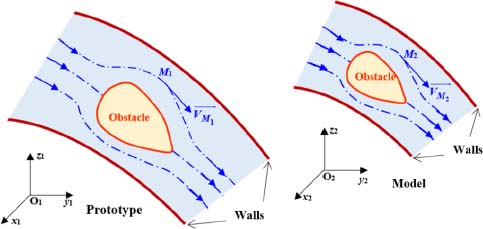
Figure 3.1. Similarity of two flows. For a color version of this figure, see www.iste.co.uk/sadchemloul/mechanics.zip

NOTE 3.1.– It is impossible to obtain a complete geometric similarity, because it is not possible to create a model that perfectly represents the state of the surface for the walls of a structure.

3.1.2. Kinematic similarity

This similarity concerns the streamlines and the trajectories, and consequently, the velocity field.

Two flows are kinematically similar when, regardless of the hom ologous point pairs (M₁ and M₂)¹ considered, the relationship ...