Design Theory, 2nd Edition

3

Quasigroup Identities and Graph Decompositions

 

3.1 Quasigroup identities

Let ( Q , ∘ ) be a quasigroup oforder n and define an n ² × 3 array R by: ( a , b , c ) ∈ R if and only if a ∘ b = c . Since a ∘ x = b and y ∘ a = b have unique solutions for all a, b ∊ Q the ordered pair ( a , b ) occurs in the same row of any two columns of R. Put another way, if we run our fingers down any two columns of R we obtain all n ² ordered pairs ( a , b ) ∈ Q × Q .

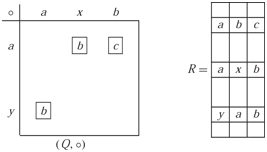
The converse is also true. Let R be an n ² × 3 array based on Q with the property that each ordered pair ( a , b ) appears in the same row in every ...