Design for Embedded Image Processing on FPGAs, 2nd Edition

11Linear Transforms

Linear transformation extends and generalises local linear filtering of Eq. (9.4) by removing the restriction of the window. Each output value is a linear combination of all of the input pixel values:

(11.1)

This enables linear transforms to separate different components of an image, for example separating signal from interference or noise.

Direct implementation of Eq. (11.1) is very expensive. For an input image, each output value requires multiplications and additions. Therefore, an output requires operations. Many useful transforms are separable in that they can be decomposed into separate, independent, one‐dimensional transforms on the rows and columns. In this case, Eq. (11.1) simplifies to

(11.2)

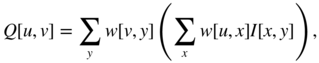
reducing the number of operations to . Separable transforms ...