Data Structures and Algorithms with JavaScript

Chapter 4. Stacks

Lists are a natural form of organization for data. We have already seen how to use the List class to organize data into a list. When the order of the data being stored doesn’t matter, or when you don’t have to search the data stored, lists work wonderfully. For other applications, however, plain lists are too simple and we need a more complex, list-like data structure.

A list-like structure that can be used to solve many problems in computing is the stack. Stacks are efficient data structures because data can be added or removed only from the top of a stack, making these procedures fast and easy to implement. Stacks are used extensively in programming language implementations for everything from expression evaluation to handling function calls.

Stack Operations

A stack is a list of elements that are accessible only from one end of the list, which is called the top. One common, real-world example of a stack is the stack of trays at a cafeteria. Trays are always removed from the top, and when trays are put back on the stack after being washed, they are placed on the top of the stack. The stack is known as a last-in, first-out (LIFO) data structure.

Because of the last-in, first-out nature of the stack, any element that is not currently at the top of the stack cannot be accessed. To get to an element at the bottom of the stack, you have to dispose of all the elements above it first.

The two primary operations of a stack are adding elements to a stack and taking elements off a stack. Elements are added to a stack using the push operation. Elements are taken off a stack using the pop operation. These operations are illustrated in Figure 4-1.

Figure 4-1. Pushing and popping elements of a stack

Another common operation on a stack is viewing the element at the top of a stack. The pop operation visits the top element of a stack, but it permanently removes the element from a stack. The peek operation returns the value stored at the top of a stack without removing it from the stack.

To keep track of where the top element is, as well as keeping track of where to add a new element, we use a top variable that is incremented when we push new elements onto the stack and is decremented when we pop elements off the stack.

While pushing, popping, and peeking are the primary operations associated with a stack, there are other operations we need to perform and properties we need to examine. The clear operation removes all the elements from a stack. The length property holds the number of elements contained in a stack. We also define an empty property to let us know if a stack has no elements in it, though we can use the length property for this as well.

A Stack Implementation

To build a stack, we first need to decide on the underlying data structure we will use to store the stack elements. We will use an array in our implementation.

We begin our stack implementation by defining the constructor function for a Stack class:

function Stack() {
   this.dataStore = [];
   this.top = 0;
   this.push = push;
   this.pop = pop;
   this.peek = peek;
}

The array that stores the stack elements is named dataStore. The constructor sets it to an empty array. The top variable keeps track of the top of the stack and is initially set to 0 by the constructor, indicating that the 0 position of the array is the top of the stack, at least until an element is pushed onto the stack.

The first function to implement is the push() function. When we push a new element onto a stack, we have to store it in the top position and increment the top variable so that the new top is the next empty position in the array. Here is the code:

function push(element) {
   this.dataStore[this.top++] = element;
}

Pay particular attention to the placement of the increment operator after the call to this.top. Placing the operator there ensures that the current value of top is used to place the new element at the top of the stack before top is incremented.

The pop() function does the reverse of the push() function—it returns the element in the top position of the stack and then decrements the top variable:

function pop() {
    return this.dataStore[--this.top];
}

The peek() function returns the top element of the stack by accessing the element at the top-1 position of the array:

function peek() {
	return this.dataStore[this.top-1];
}

If you call the peek() function on an empty stack, you get undefined as the result. That’s because there is no value stored at the top position of the stack since it is empty.

There will be situations when you need to know how many elements are stored in a stack. The length() function returns this value by returning the value of top:

function length() {
	return this.top;
}

Finally, we can clear a stack by simply setting the top variable back to 0, and setting the dataStore array’s length to zero:

function clear() {
	this.top = 0;
    this.dataStore.length = 0;
}

Example 4-1 shows the complete implementation of the Stack class.

Example 4-1. The Stack class

load("Stack.js");

function Stack() {
   this.dataStore = [];
   this.top = 0;
   this.push = push;
   this.pop = pop;
   this.peek = peek;
   this.clear = clear;
   this.length = length;
}

function push(element) {
   this.dataStore[this.top++] = element;
}

function peek() {
   return this.dataStore[this.top-1];
}

function pop() {
   return this.dataStore[--this.top];
}

function clear() {
   this.top = 0;
   this.dataStore.length = 0;
}

function length() {
   return this.top;
}

Example 4-2 demonstrates a program that tests this implementation.

Example 4-2. Testing the Stack class implementation

load("Stack.js");

var s = new Stack();
s.push("David");
s.push("Raymond");
s.push("Bryan");
print("length: " + s.length());
print(s.peek());
var popped = s.pop();
print("The popped element is: " + popped);
print(s.peek());
s.push("Cynthia");
print(s.peek());
s.clear();
print("length: " + s.length());
print(s.peek());
s.push("Clayton");
print(s.peek());

The output from Example 4-2 is:

length: 3
Bryan
The popped element is: Bryan
Raymond
Cynthia
length: 0
undefined
Clayton

The next-to-last value, undefined, is returned because once a stack is cleared, there is no value in the top position and when we peek at the top of the stack, undefined is returned.

Using the Stack Class

There are several problems for which a stack is the perfect data structure needed for the solution. In this section, we look at several such problems.

Multiple Base Conversions

A stack can be used to convert a number from one base to another base. Given a number, n, which we want to convert to a base, b, here is the algorithm for performing the conversion:

1. The rightmost digit of n is n % b. Push this digit onto the stack.

2. Replace n with n / b.

3. Repeat steps 1 and 2 until n = 0 and there are no significant digits remaining.

4. Build the converted number string by popping the stack until the stack is empty.

Note

This algorithm will work only with bases 2 through 9.

We can implement this algorithm very easily using a stack in JavaScript. Here is the definition of a function for converting a number to any of the bases 2 through 9:

function mulBase(num, base) {
   var s = new Stack();
   do {
      s.push(num % base);
      num = Math.floor(num /= base);
   } while (num > 0);
   var converted = "";
   while (s.length() > 0) {
      converted += s.pop();
   }
   return converted;
}

Example 4-3 demonstrates how to use this function for base 2 and base 8 conversions.

Example 4-3. Converting numbers to base 2 and base 8

load("Stack.js");

function mulBase(num, base) {
   var s = new Stack();
   do {
      s.push(num % base);
      num = Math.floor(num /= base);
   } while (num > 0);
   var converted = "";
   while (s.length() > 0) {
      converted += s.pop();
   }
   return converted;
}

var num = 32;
var base = 2;
var newNum = mulBase(num, base);
print(num + " converted to base " + base + " is " + newNum);
num = 125;
base = 8;
var newNum = mulBase(num, base);
print(num + " converted to base " + base + " is " + newNum);

The output from Example 4-3 is:

32 converted to base 2 is 100000
125 converted to base 8 is 175

Palindromes

A palindrome is a word, phrase, or number that is spelled the same forward and backward. For example, “dad” is a palindrome; “racecar” is a palindrome; “A man, a plan, a canal: Panama” is a palindrome if you take out the spaces and ignore the punctuation; and 1,001 is a numeric palindrome.

We can use a stack to determine whether or not a given string is a palindrome. We take the original string and push each character onto a stack, moving from left to right. When the end of the string is reached, the stack contains the original string in reverse order, with the last letter at the top of the stack and the first letter at the bottom of the stack, as shown in Figure 4-2.

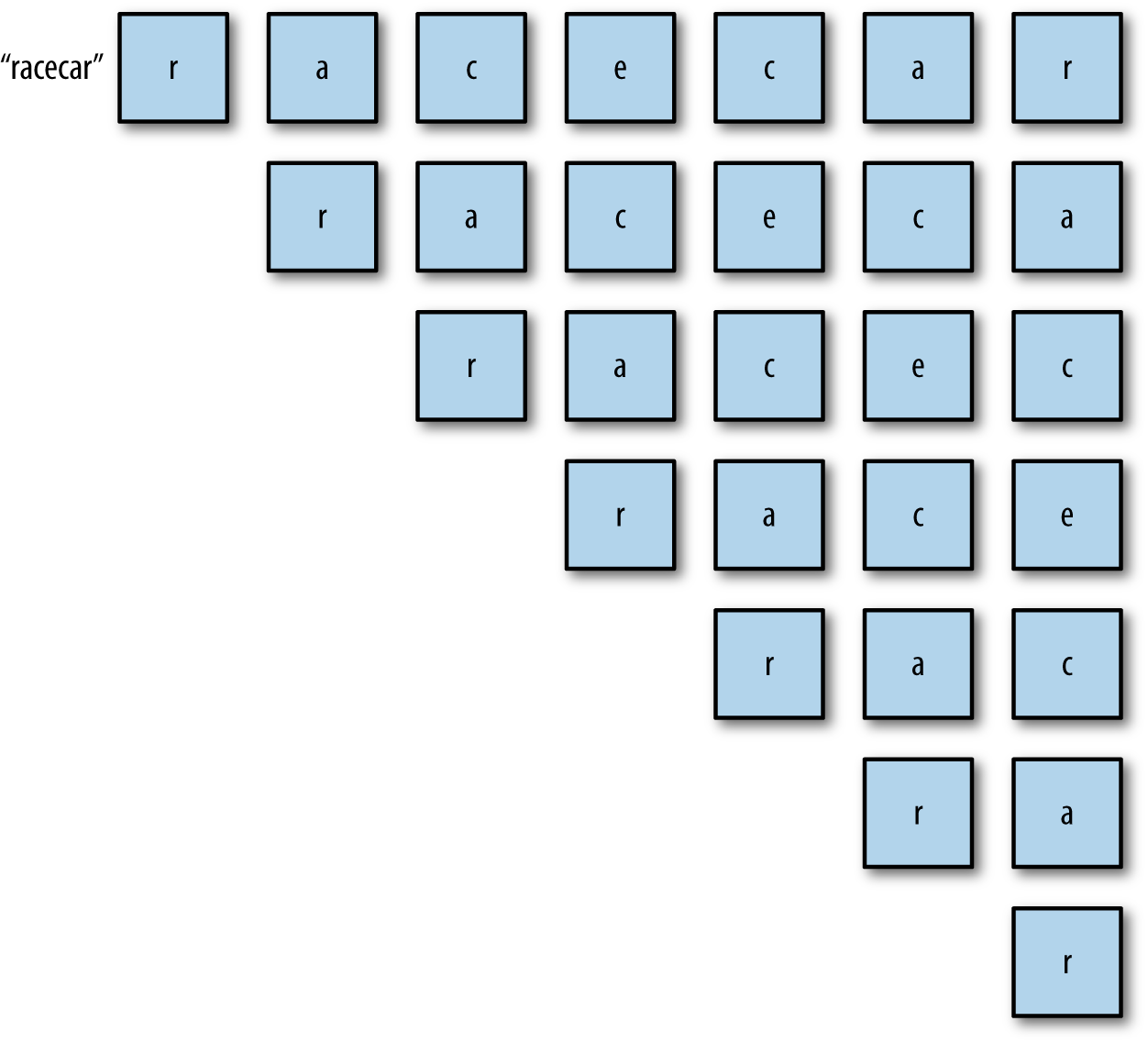
Figure 4-2. Using a stack to determine if a word is a palindrome

Once the complete original string is on the stack, we can create a new string by popping each letter the stack. This process will create the original string in reverse order. We then simply compare the original string with the reversed work, and if they are equal, the string is a palindrome.

Example 4-4 presents a program, minus the Stack class code, that determines if a given string is a palindrome.

Example 4-4. Determining if a string is a palindrome

load ("Stack.js");

function isPalindrome(word) {
   var s = new Stack();
   for (var i = 0; i < word.length; ++i) {
      s.push(word[i]);
   }
   var rword = "";
   while (s.length() > 0) {
      rword += s.pop();
   }
   if (word == rword) {
      return true;
    }
   else {
      return false;
   }
}

var word = "hello";
if (isPalindrome(word)) {
   print(word + " is a palindrome.");
}
else {
   print(word + " is not a palindrome.");
}
word = "racecar"
if (isPalindrome(word)) {
   print(word + " is a palindrome.");
}
else {
   print(word + " is not a palindrome.");
}

The output from this program is:

hello is not a palindrome.
racecar is a palindrome.

Demonstrating Recursion

Stacks are often used in the implementation of computer programming languages. One area where stacks are used is in implementing recursion. It is beyond the scope of this book to demonstrate exactly how stacks are used to implement recursive procedures, but we can use stacks to simulate recursive processes. If you are interested in learning more about recursion, a good starting point is this web page that actually uses JavaScript to describe how recursion works.

To demonstrate how recursion is implemented using a stack, let’s consider a recursive definition of the factorial function. First, here is a definition of factorial for the number 5:

5! = 5 * 4 * 3 * 2 * 1 = 120

Here is a recursive function to compute the factorial of any number:

function factorial(n) {
   if (n === 0) {
      return 1;
   }
   else {
      return n * factorial(n-1);
   }
}

When called with the argument 5, the function returns 120.

To simulate computing 5! using a stack, first push the numbers 5 through 1 onto a stack. Then, inside a loop, pop each number and multiply the number by the running product, resulting in the correct answer, 120. Example 4-5 contains the code for the function, along with a test program.

Example 4-5. Simulating recursive processes using a stack

load("Stack.js");

function factorial(n) {
   if (n === 0) {
      return 1;
   }
   else {
      return n * factorial(n-1);
   }
}

function fact(n) {
   var s = new Stack();
   while (n > 1) {
      s.push(n--);
   }
   var product = 1;
   while (s.length() > 0) {
      product *= s.pop();
   }
   return product;
}

print(factorial(5)); // displays 120
print(fact(5)); // displays 120

Exercises

1. A stack can be used to ensure that an arithmetic expression has balanced parentheses. Write a function that takes an arithmetic expression as an argument and returns the postion in the expression where a parenthesis is missing. An example of an arithmetic expression with unbalanced parentheses is 2.3 + .

2. A postfix expression evaluator works on arithmetic expressions taking the following form:

   op1 op2 operator

   Using two stacks—one for the operands and one for the operators—design and implement a JavaScript function that converts infix expressions to postfix expressions, and then use the stacks to evaluate the expression.

3. An example of a real-world stack is a Pez dispenser. Imagine that your virtual Pez dispenser is filled with red, yellow, and white colors and you don’t like the yellow ones. Write a program that uses a stack (and maybe more than one) to remove the yellow ones without changing the order of the other candies in the dispenser.