Capítulo 1. Introducción Introducción
Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: translation-feedback@oreilly.com
Se calcula que entre el 70% y el 80% de las ofertas de empleo para un analista de datos mencionan la estadística como habilidad o requisito deseado. Yo mismo no he encontrado la forma de probar esas cifras, pero si nos fijamos en las ofertas de empleo, estaría a favor de esa estimación. Con cantidades de datos cada vez mayores, las empresas buscan formas de interpretar y comprender esos datos. La estadística suele ser la forma más científica de hacerlo. Sin embargo, creo que a muchos analistas y desarrolladores de Tableau les cuesta implementar la estadística en sus análisis o visualizaciones de datos. Hay muchas razones para ello, y seré el primero en decirte que no es por falta de ganas. Las estadísticas pueden intimidar tanto a los desarrolladores como a las partes interesadas que confían en sus informes. Tratar de explicar e interpretar complejas ecuaciones estadísticas es difícil sin una firme comprensión de la disciplina.
Ése es exactamente el propósito de este libro. Quiero dotarte de esa firme comprensión de la estadística y darte la confianza necesaria para hablar con las ecuaciones e implementarlas en tu trabajo. En este libro, me centraré en combinar la visualización de datos en Tableau con el análisis estadístico para que puedas respaldar tus ideas con pruebas científicas.
En este capítulo, te presentaré algunos términos comunes de Tableau que utilizaré a lo largo del libro. También te presentaré algunas ideas y términos estadísticos básicos. Hacia el final del capítulo, te presentaré un caso práctico que vincula ambas disciplinas, y hablaré de la importancia de visualizar los resultados estadísticos.
Introducción a Tableau
Es importante entender que Tableau no es simplemente una herramienta de visualización de datos, sino una empresa con un conjunto de herramientas para apoyar la visualización y el análisis de datos a nivel empresarial. Hay muchos productos dentro del ecosistema de Tableau, como Tableau Desktop, Tableau Cloud, Tableau Server, Tableau Prep Builder y Tableau Public, entre otros.
Algunos de estos productos requieren una licencia para su uso, mientras que otros, como Tableau Public, no requieren que adquieras una licencia, pero tienen ciertas limitaciones. Con una licencia, puedes publicar tus libros de trabajo en Tableau Server o Tableau Cloud desde Tableau Desktop. Esto permite a tus usuarios ver e interactuar con tus visualizaciones de datos desde un navegador. Consulta el sitio web de Tableau para obtener una lista completa de todos los productos de Tableau .
Términos comunes de la interfaz de autor de Tableau Desktop
Hay varios términos comunes dentro de Tableau Desktop que quiero que conozcas y con los que te familiarices. Para empezar, cuando abras Tableau Desktop, aterrizarás en la Página de Inicio, como se muestra en la Figura 1-1.
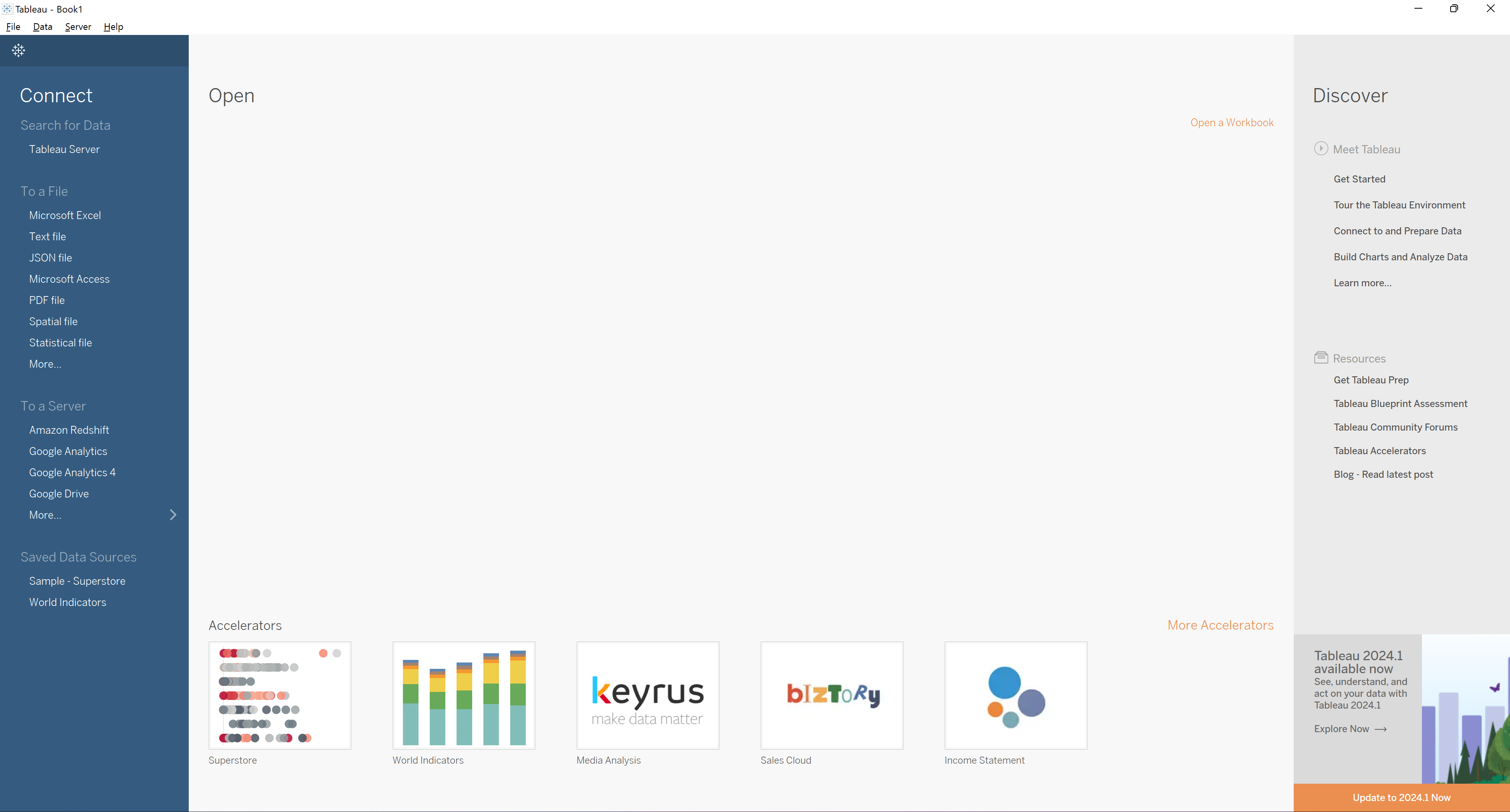
Figura 1-1. Página de inicio de Tableau Desktop
Desde la Página de inicio, puedes conectar a los datos que quieras visualizar. Tableau dispone de cientos de conectores que puedes utilizar para acceder a tus datos. Un conector es básicamente como una API integrada que te permite establecer una conexión con una base de datos o un tipo de archivo para leer esos datos en Tableau Desktop. En la parte izquierda de la página de inicio puedes explorar todos los conectores disponibles.
Para todas las demostraciones de este libro, utilizaré el conjunto de datos Muestra - Supertienda. Para conectarte a este conjunto de datos, sólo tienes que hacer clic en Muestra - Supertienda, como se muestra en la Figura 1-2.

Figura 1-2. Conexión a la Muestra - Supertienda
Es importante tener en cuenta que si utilizas una versión de Tableau Desktop distinta a la mía, es posible que obtengas resultados diferentes. Tableau actualizará ocasionalmente el conjunto de datos Muestra - Supertienda. Yo utilizaré la versión 2023.2 a lo largo de este libro. Si quieres seguirlo exactamente, puedes descargar esta versión de la página de soporte de productos de Tableau.
Después de hacer clic en el conjunto de datos de muestra, serás dirigido desde la Página de Inicio a la interfaz de creación de Tableau Desktop, como se muestra en la Figura 1-3.
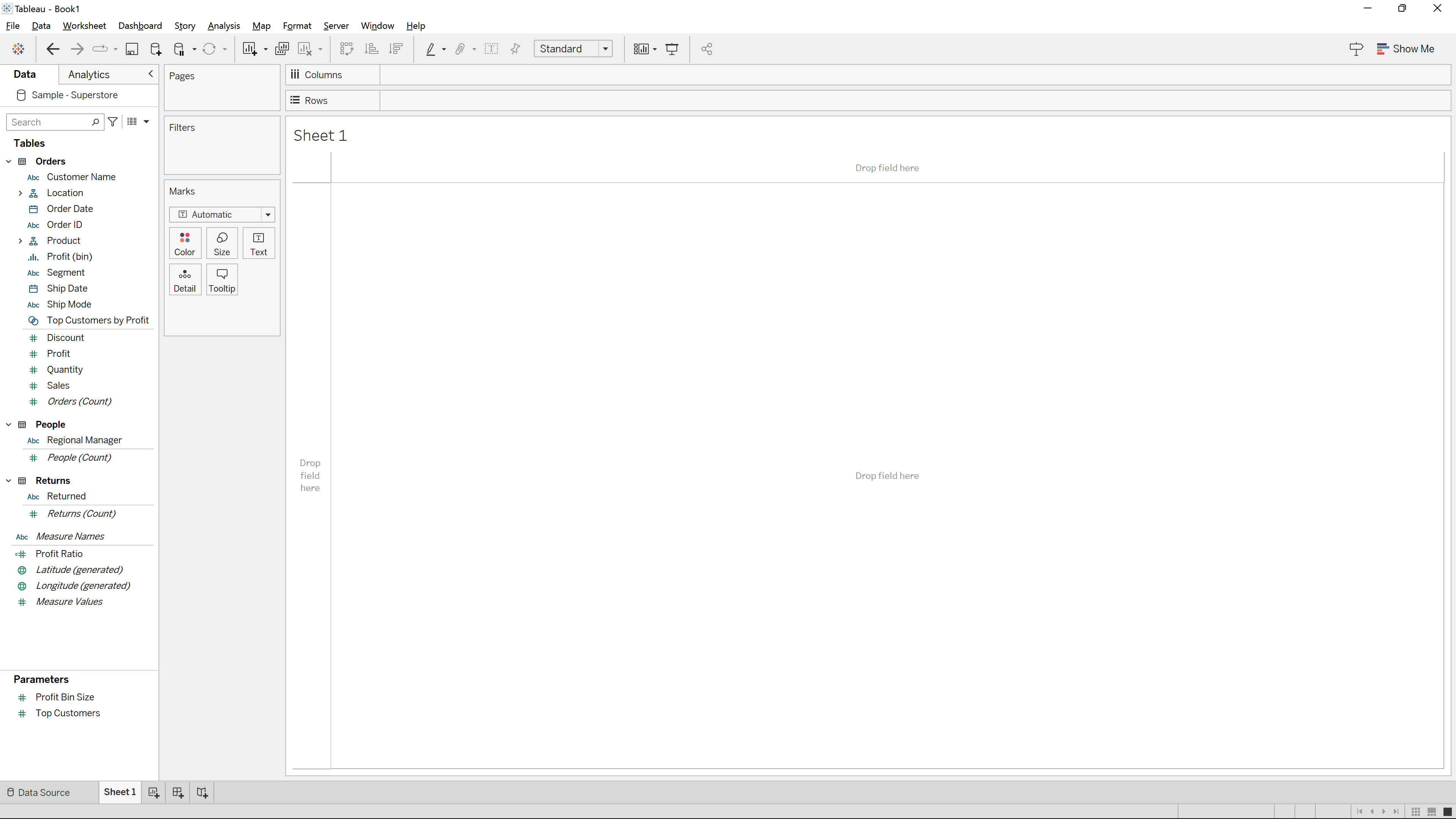
Figura 1-3. Interfaz de creación de Tableau Desktop
Para introducirte en los términos que utilizaré a lo largo del libro, en la parte izquierda encontrarás el panel de Datos, como se muestra en la Figura 1-4.
En la parte superior del panel Datos, verás una lista de las fuentes de datos a las que estás conectado. Desplazándote hacia abajo, encontrarás una lista de campos, incluidos los calculados, separados por fuente de datos y por si Tableau considera que ese campo es una medida o una dimensión.
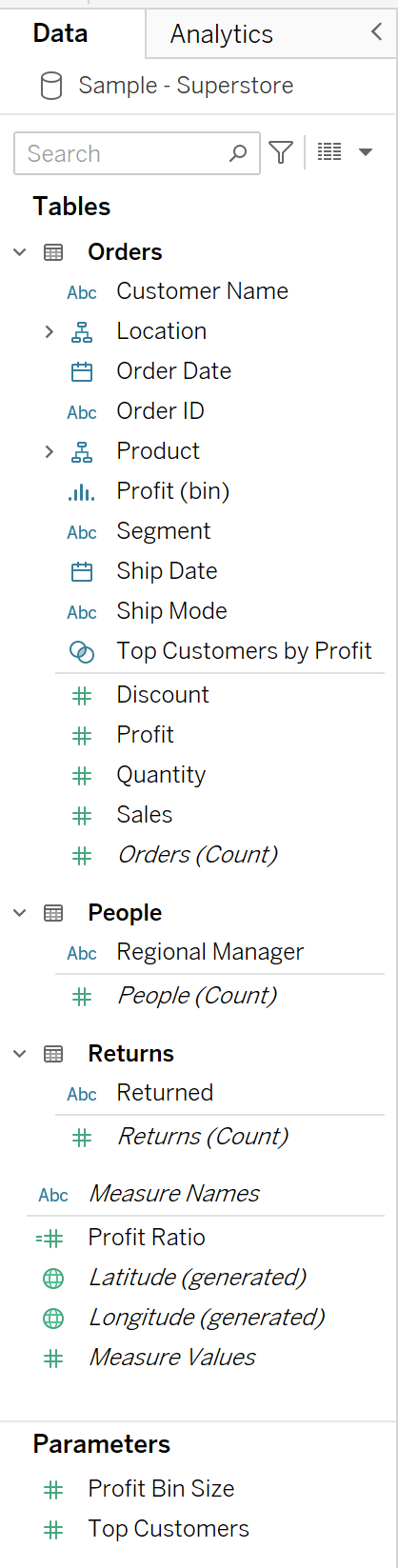
Figura 1-4. El panel Datos de la interfaz de creación
A la derecha del panel de Datos, encontrarás los distintos componentes utilizados para crear visualizaciones, llamados estantes. Están la estantería Marcas, la estantería Filtros, la estantería Páginas, la estantería Columnas, la estantería Filas y el lienzo, como se muestra en la Figura 1-5.
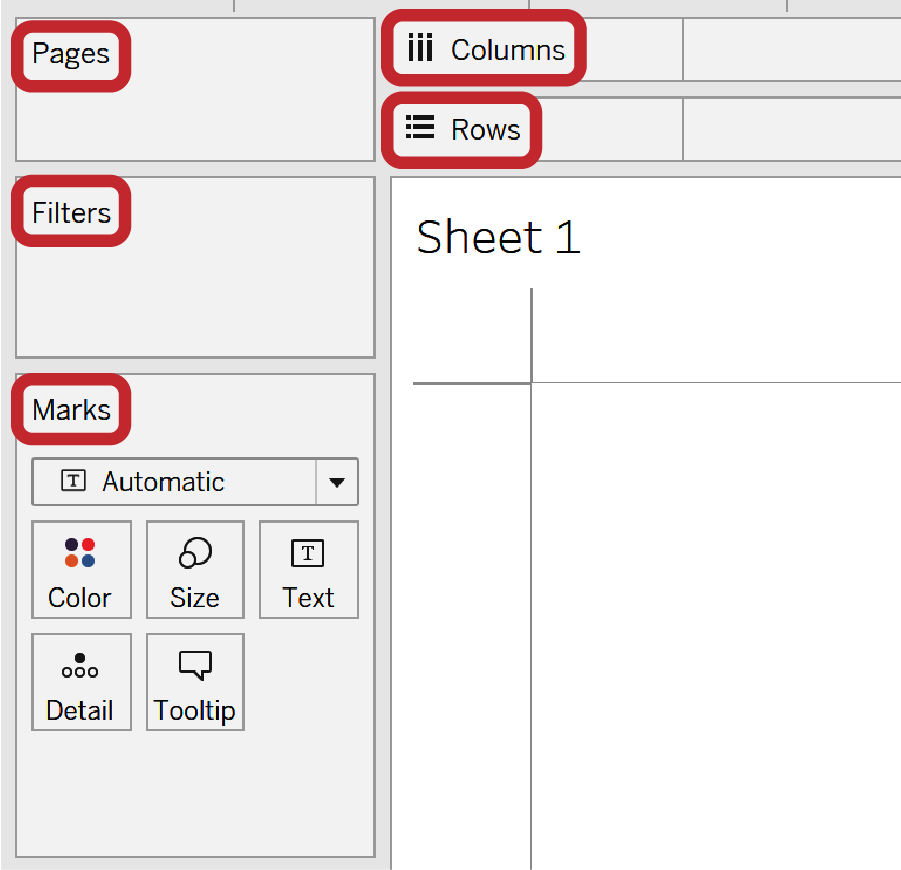
Figura 1-5. Características principales de la interfaz de creación
Para definirlos un poco más, he aquí una breve explicación de cada uno:
- Estante de marcas
-
El estante Marcas es un elemento clave de en la interfaz de creación y te permite arrastrar campos a diferentes propiedades que afectan a la vista. Las propiedades son Color, Tamaño, Texto, Detalle y Tooltip. Hay diferentes opciones de propiedades que aparecerán cuando se cumplan determinadas condiciones. Por ejemplo, al cambiar el tipo de Marca a polígono, verás una nueva propiedad de ángulo en el estante Marcas.
- Filtros estantería
-
La estantería Filtros te permite añadir diferentes campos para filtrar la vista. Hay ocho tipos diferentes de filtros en Tableau que se procesan en momentos distintos en el orden de operaciones de Tableau.
- Estante de páginas
-
El estante Páginas te permite dividir la vista en páginas para que puedas analizar cómo afecta un campo concreto al resto de los campos de la vista. El uso más común de esto es añadir una dimensión Fecha y animar cómo cambian las cosas con el tiempo.
- Estante de columnas
-
El estante Columnas es donde puedes arrastrar campos para crear las columnas de la visualización que estás haciendo. El estante Columnas se coordinará con el eje x de la visualización.
- Estante de filas
-
El estante Filas es donde puedes arrastrar campos para crear las filas de la visualización que estás haciendo. El estante Filas se coordina con el eje y de la vista.
- Lienzo
-
El lienzo es donde aparecerá la visualización de datos cuando empieces a arrastrar campos a las demás estanterías. También puedes arrastrar diferentes campos directamente al lienzo cuando estés creando una visualización de datos. Al hacerlo, añadirás el campo a la estantería adecuada para ti.
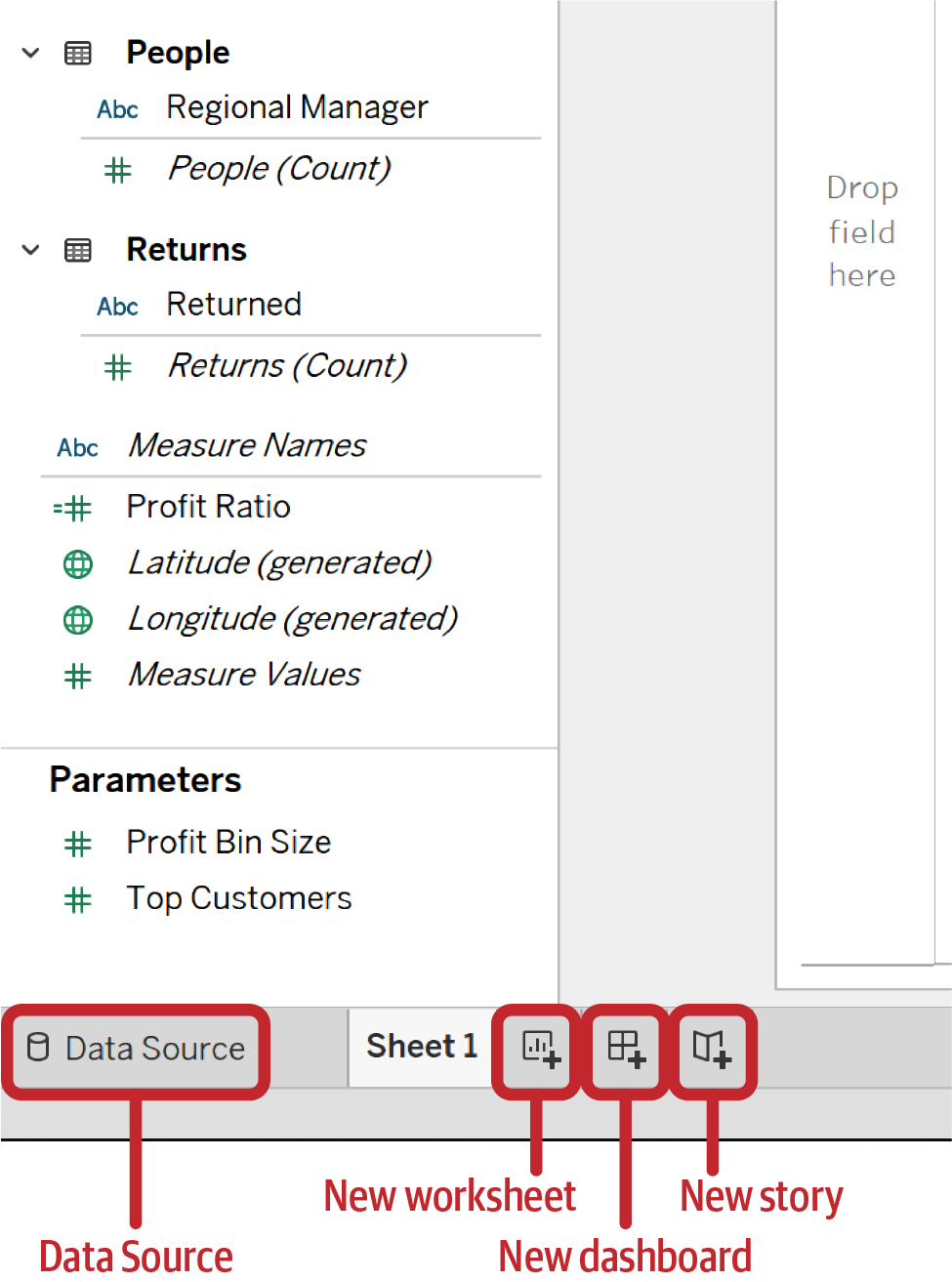
La última característica importante que quiero destacar en este capítulo se encuentra en la esquina inferior izquierda de la interfaz de creación. Allí encontrarás un botón para navegar a la página de la fuente de datos y tres botones adicionales. Estos botones se utilizan para crear nuevas hojas de cálculo, nuevos cuadros de mando o nuevas historias, como se muestra en la Figura 1-6.
Para darte un poco más de contexto, aquí tienes una breve descripción de cada uno:
- Botón Fuente de datos
-
Esto te llevará a la página Fuente de datos. Desde ahí, puedes añadir nuevas conexiones, crear nuevas fuentes de datos y ver la capa física y lógica para las uniones y mezclas.
- Botón Nueva hoja de cálculo
-
Al hacer clic en este botón se creará una nueva hoja de cálculo y navegarás a la pestaña de esa hoja. Desde aquí puedes crear una nueva visualización de datos.
- Nuevo botón del salpicadero
-
Al seleccionar este botón se creará un nuevo panel de control y navegarás a la pestaña de ese panel. Desde aquí puedes arrastrar hojas al lienzo en lugar de campos para compilar un nuevo cuadro de mando.
- Botón de nueva historia
-
Al hacer clic en el botón de nueva historia se creará una nueva historia y navegarás a la pestaña de esa historia. Desde aquí, puedes compilar una historia utilizando hojas o cuadros de mando para crear diferentes páginas dentro de tu historia.
Ejemplo de las instrucciones paso a paso a lo largo de este libro
Para que te familiarices con las instrucciones de y con el estilo de escritura utilizado en este libro, en esta sección se ofrece un ejemplo sencillo que agrupa los términos más comunes. Utilizar Tableau Desktop es muy intuitivo, y hay muchas formas diferentes de hacer las cosas. Voy a mostrarte cómo crear dos gráficos sencillos y añadirlos a un dashboard utilizando el conjunto de datos Muestra - Supertienda. Supongamos que quieres ver las ventas por fecha de pedido. En primer lugar, haz doble clic en Ventas en el panel de Datos y, a continuación, haz doble clic en Fecha de pedido, como se muestra en la Figura 1-7.
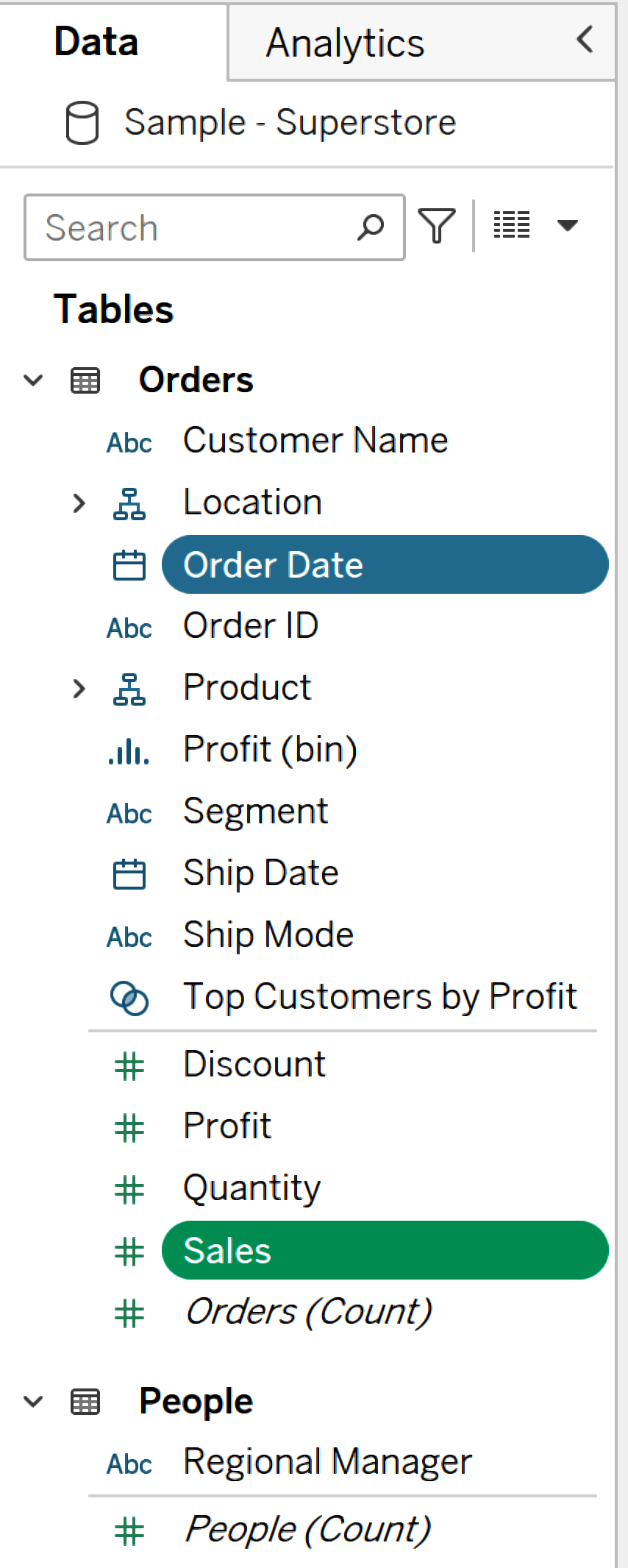
Figura 1-7. Haciendo clic en Ventas y Fecha de pedido en la vista
Tableau es lo suficientemente intuitivo como para reconocer que probablemente quieras que estos datos muestren una tendencia a lo largo del tiempo, y creará automáticamente un gráfico de líneas, como se muestra en la Figura 1-8.
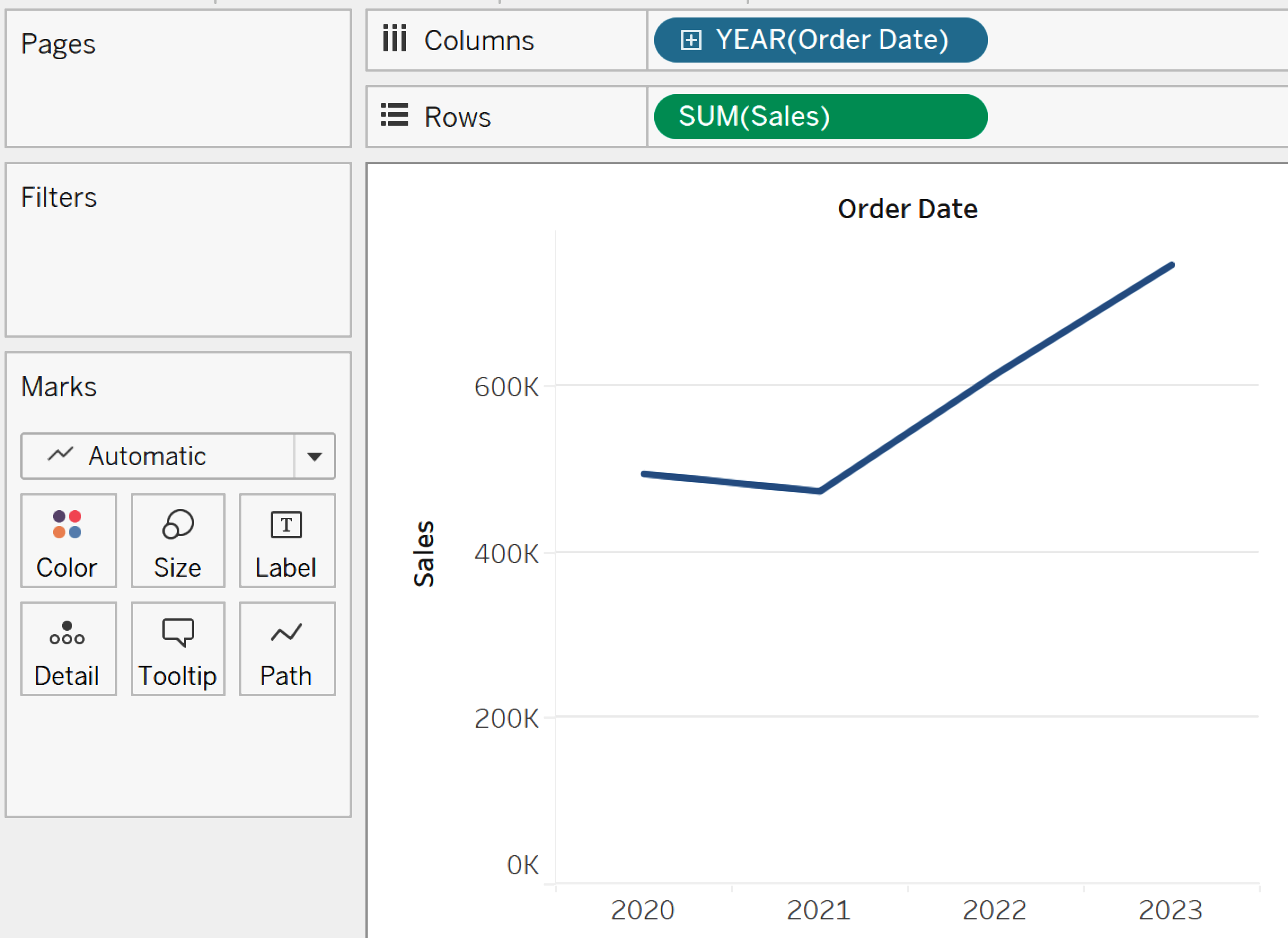
Figura 1-8. Crear un gráfico de líneas sencillo en Tableau Desktop
Supongamos ahora que también quieres ver tus datos de ventas por segmentos. Haz clic en el botón "Nueva hoja de cálculo" situado en la parte inferior izquierda de la interfaz de creación, como se muestra en la Figura 1-9.
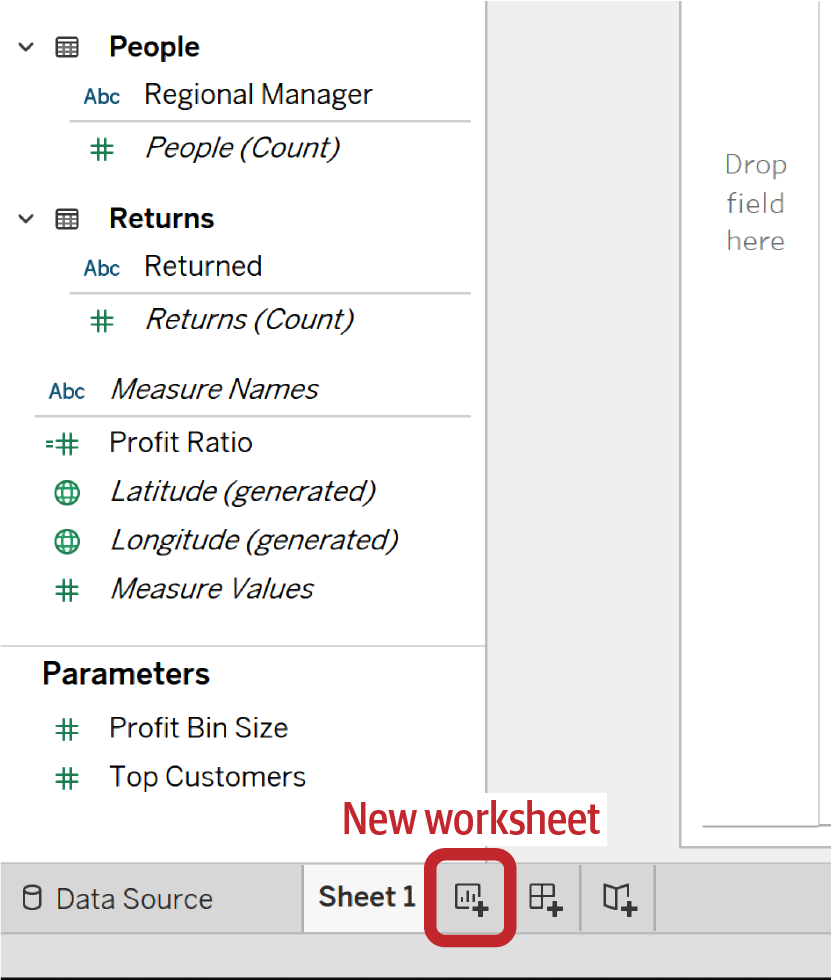
Figura 1-9. Crear una nueva hoja desde la interfaz de creación
Esto abrirá la Hoja 2; tu primer gráfico todavía se puede ver navegando de vuelta a la Hoja 1. Haz doble clic en Ventas y luego en Segmento en el panel de Datos, como se muestra en la Figura 1-10.
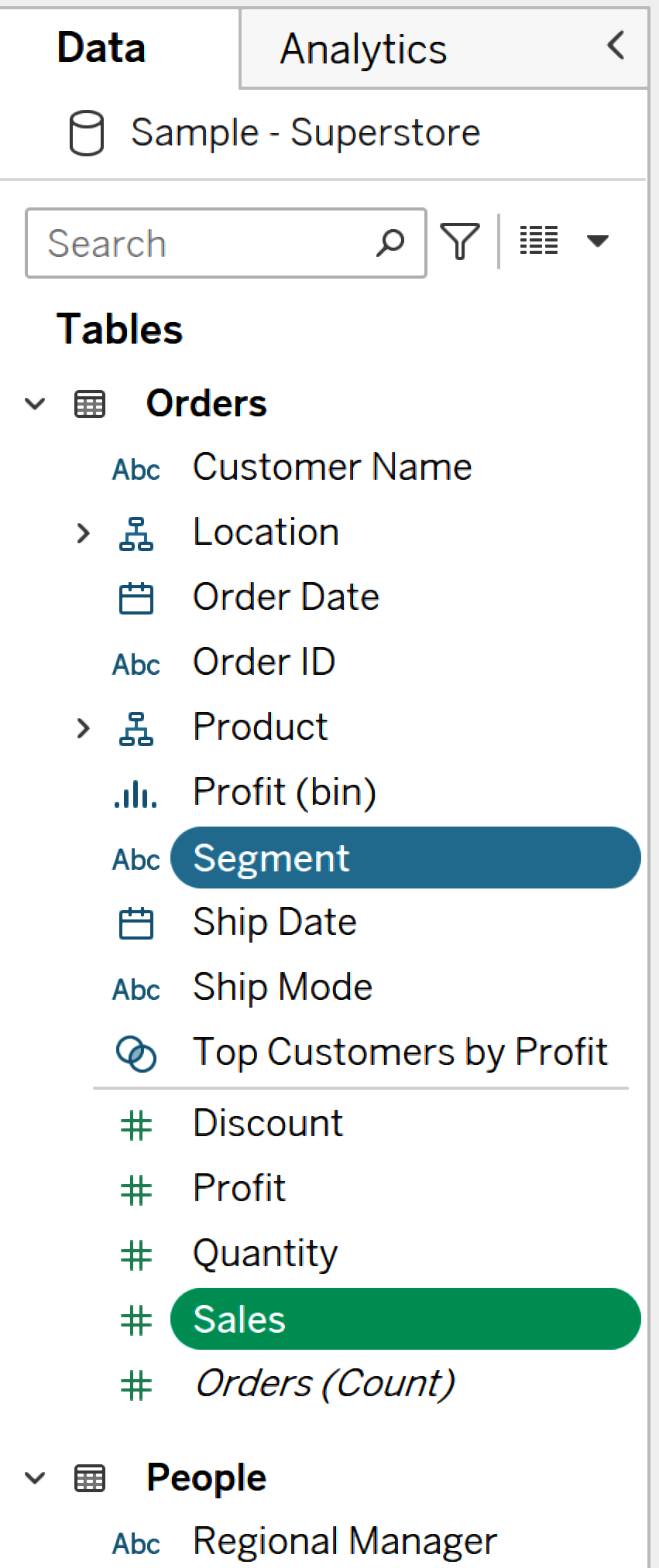
Figura 1-10. Haciendo clic en Segmento y Ventas del panel Datos
Esto creará un sencillo gráfico de barras que mostrará la SUM(Ventas) (suma de ventas) por Segmento en el lienzo, similar a la Figura 1-11.
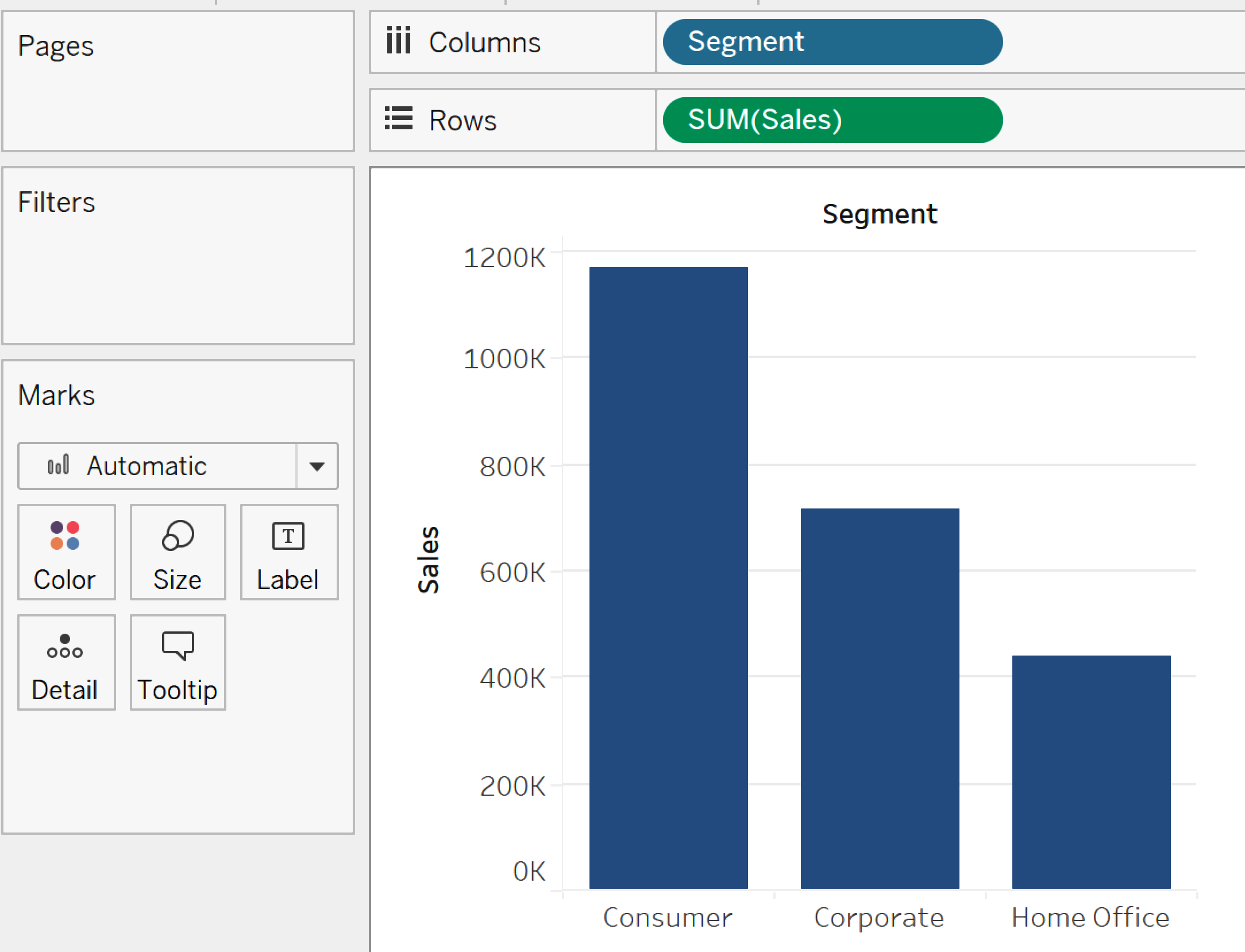
Figura 1-11. Crear un gráfico de barras sencillo en Tableau Desktop
Hasta ahora, has podido ver estos dos gráficos en un entorno de trabajo en Tableau. Supongamos que quieres compartir estos gráficos con otras personas de tu organización. Para iniciar ese proceso, haz clic en el botón "Nuevo dashboard" de la parte inferior izquierda de la interfaz de creación, como se muestra en la Figura 1-12.
Figura 1-12. Crear un nuevo cuadro de mando desde la interfaz de creación
Se abrirá un nuevo lienzo en el que podrás crear cuadros de mando, como se muestra en la Figura 1-13. Los cuadros de mando son el pan de cada día de Tableau y, en última instancia, lo que compartirás para que los usuarios interactúen con ellos.
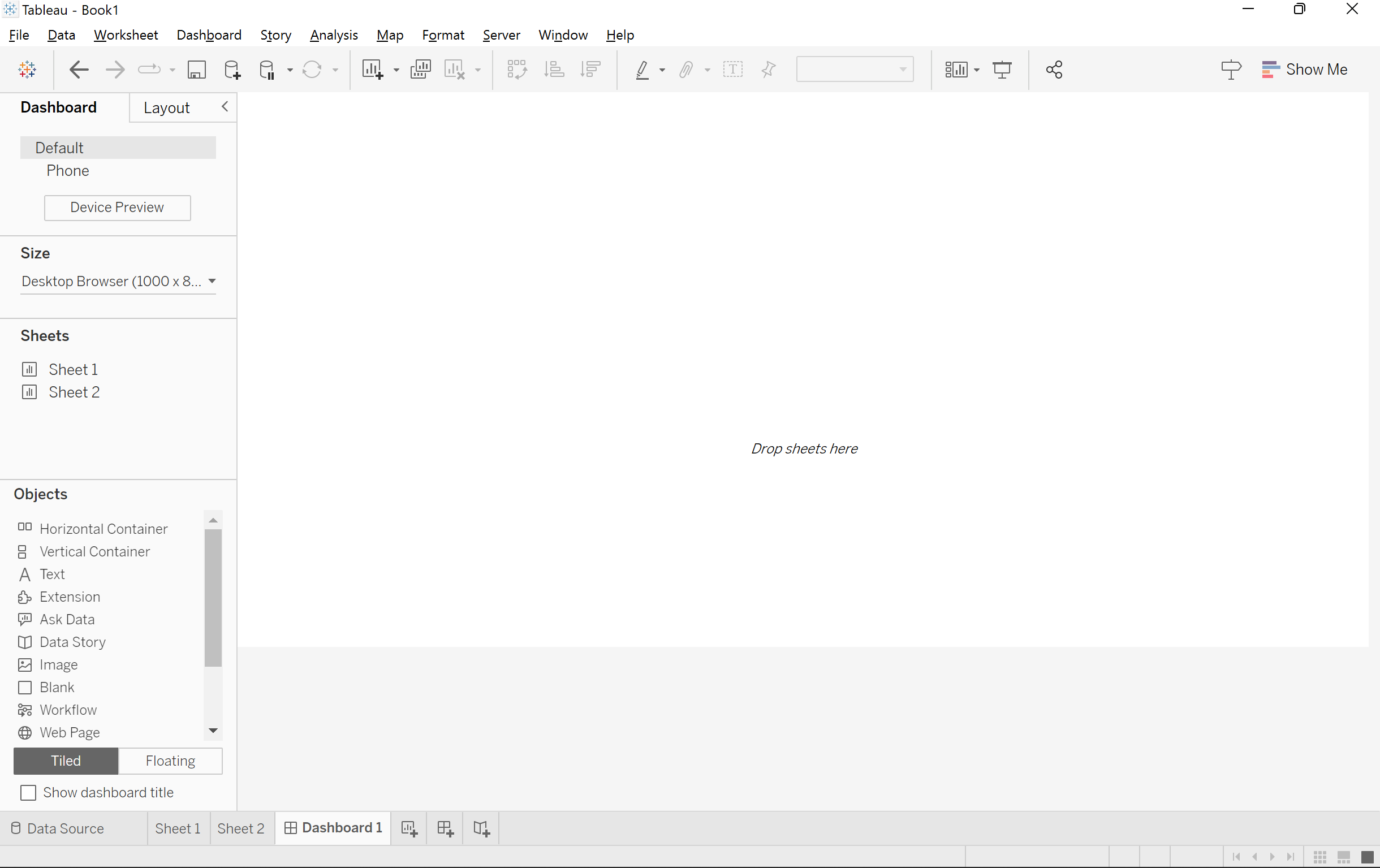
Figura 1-13. Lienzo del panel de control en Tableau Desktop
Ahora añade tus dos hojas en el lienzo del panel de control. A la izquierda, haz clic y arrastra la Hoja 1 al lienzo. A continuación, haz clic y arrastra la Hoja 2 al lienzo. Tu panel de control debería parecerse ahora a la Figura 1-14.
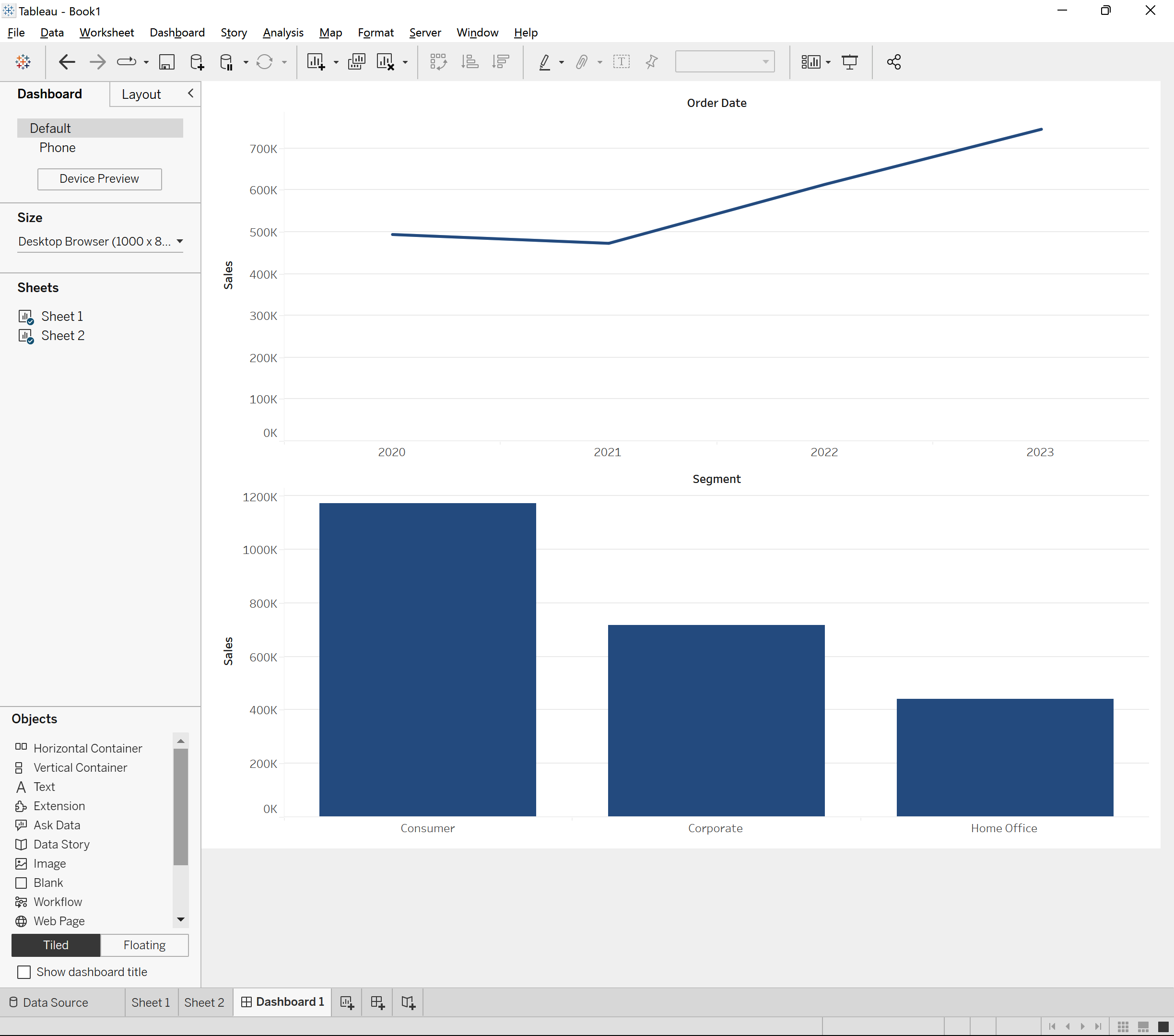
Figura 1-14. Crear un diseño de panel sencillo en Tableau Desktop
Este ejemplo debería ayudarte a ver cómo se utilizarán los términos comunes de Tableau en los tutoriales a lo largo de este libro. Conocer la disposición de la herramienta y los términos es la base para comprender Tableau Desktop en su conjunto. Lo más probable es que el contenido hasta ahora te haya servido de repaso. A partir de ahora, te mostraré cómo integrar las estadísticas en tus cuadros de mando y te daré ejemplos tangibles de cómo aplicarlas en tu trabajo. En la siguiente sección, te presentaré términos estadísticos comunes y te mostraré un ejemplo que lo relaciona todo.
Introducción a la Estadística
Según el diccionario en línea Merriam-Webster , la estadística se define como una rama de las matemáticas que se ocupa de la recopilación, el análisis, la interpretación y la presentación de masas de datos numéricos. Personalmente, creo que esta definición da en el clavo, especialmente en el entorno empresarial actual. Para desentrañar la profundidad de tus datos, necesitas incorporar la estadística a casi todos los aspectos del proceso analítico. Esto incluye la recopilación de datos de forma eficaz y ética, la comprensión de los datos, la búsqueda de perspectivas más profundas en el análisis y la presentación de tus conclusiones para que las partes interesadas puedan tomar decisiones con conocimiento de causa.
En la siguiente sección, te presentaré algunos términos e ideas estadísticos comunes. También te mostraré lo poderoso que puede ser añadir estadísticas a tu análisis mediante un ejemplo tangible de estudio de caso.
Términos estadísticos comunes
Para nivelar, explicaré brevemente algunos de estos términos e ideas. Sin embargo, no se trata de una lista exhaustiva de todo lo que hay que saber sobre estadística. El propósito de este libro es que te sientas más cómodo y te familiarices con los fundamentos de la estadística para que puedas aplicarlos a tu propio trabajo. También entraré en más detalles sobre algunos de estos términos a medida que avances en cada capítulo, cuando proceda:
- Una estadística
A lo largo de este libro, verás que me refiero a diferentes cosas como una estadística. La definición de estadística es un hecho o dato procedente del estudio de una gran cantidad de datos numéricos. Esto significa que cualquier cosa que puedas calcular a partir de un gran conjunto de datos podría denominarse estadística. Por ejemplo, si calculamos la media, la mediana o la moda de un conjunto de datos, me referiría a cada uno de esos valores como una estadística.
- Comprobación de hipótesis
Establecer una prueba de hipótesis es uno de los pasos más fundamentales en la mayoría de los análisis estadísticos. Si no lo haces, te encontrarás persiguiendo algún tipo de significación estadística, cuando demostrar simplemente que no hay una diferencia significativa es igual de poderoso. Básicamente, una prueba de hipótesis consiste en crear una hipótesis nula y una hipótesis alternativa. Luego estableces las condiciones de lo que consideras una diferencia significativa a favor de una hipótesis o de la otra fijando un nivel de significación.
- Nivel de significación
Un nivel de significación es el umbral predeterminado utilizado para determinar la significación estadística. El nivel de significación más común es 0,05 (5%), pero se trata de un número arbitrario. Hay ocasiones en las que puede ser más o menos significativo. Por ejemplo, si te dedicas a la sanidad, puede que quieras mostrar resultados que tengan un nivel de significación más alto para garantizar la interpretación más precisa de los resultados.
- Significación estadística
Significación estadística es un término utilizado en estadística para determinar si es probable que un efecto o una relación observados en los datos sean auténticos o si podrían haberse producido por casualidad. En otras palabras, ayuda a los analistas a evaluar si los resultados de un análisis son significativos o si podrían atribuirse a una variación aleatoria.
Para relacionarlo con las pruebas de hipótesis:
- Valor P
-
El valor p (valor de probabilidad) es una medida de la evidencia contra una hipótesis nula. Representa la probabilidad de obtener los resultados observados (o resultados más extremos) si la hipótesis nula es cierta. Un valor p bajo (normalmente inferior a 0,05) se considera indicativo de significación estadística.
Si el valor p es inferior a el nivel de significación elegido (normalmente 0,05), se rechaza la hipótesis nula a favor de la hipótesis alternativa. Si el valor p es mayor que el nivel de significación, no hay pruebas suficientes para rechazar la hipótesis nula.
En resumen, defines qué vas a probar estableciendo una hipótesis nula y una hipótesis alternativa. Luego decides cuál debe ser el nivel de significación de tu experimento. A continuación, compruebas si hay una diferencia estadísticamente significativa y utilizas el valor p como unidad de medida en comparación con tu nivel de significación predeterminado.
Para que entiendas bien estas ideas, quiero mostrarte un ejemplo práctico que podemos calcular a mano. Así podrás ver cómo se combinan todos estos términos.
Aplicación práctica mediante un estudio de caso
Supongamos que tu empresa quiere probar un nuevo marketing en un correo electrónico. Sin embargo, les preocupa que si el nuevo marketing fracasa, pueda afectar significativamente a las ventas de este trimestre. Por tanto, quieren probar el nuevo marketing por correo electrónico enviándolo a un subconjunto de la lista total de correo electrónico, y luego analizar el rendimiento antes de decidir si siguen adelante con el nuevo marketing. La Tabla 1-1 muestra los resultados de la prueba en una tabla de contingencia.
| Correo electrónico original | Nuevo correo electrónico de marketing | |
|---|---|---|
| No conversiones | 727 | 117 |
| Conversiones | 23 | 8 |
Una tabla de contingencia es una forma de organizar y mostrar datos en formato de tabla, especialmente cuando se estudia la relación entre dos variables categóricas. Las variables categóricas son variables que representan categorías o grupos, como colores, tipos de frutas o respuestas a una pregunta de sí o no. En este ejemplo, estamos mostrando cuántas conversiones tuvo el correo electrónico original en comparación con el nuevo correo electrónico de marketing. La conversión se ha definido como "el punto en el que el destinatario de un mensaje de marketing realiza una acción deseada".1
El equipo de marketing ha realizado un sencillo análisis de las tasas de conversión de los correos electrónicos tomando el total de envíos/conversiones de cada campaña. Utilizando este cálculo, descubrieron que el correo electrónico original tenía una tasa de conversión de aproximadamente el 3% (23 ÷ 750 = 0,030) y el nuevo correo electrónico de marketing tenía una tasa de conversión de aproximadamente el 6% (8 ÷ 125 = 0,064). Afirman que el nuevo correo electrónico es un éxito absoluto y que duplicará la cantidad de conversiones cuando lo envíen a toda su lista la próxima vez.
Los altos directivos de la empresa están encantados con la idea de duplicar el volumen de ventas y quieren invertir en varios vendedores nuevos para ayudar con el aumento. Sin embargo, acuden a ti en busca de una segunda opinión y te preguntan si el equipo de análisis podría revisar los datos y confirmar las suposiciones del equipo de marketing.
¿Por dónde empezar? Aquí es donde el análisis estadístico se convertirá en tu mejor amigo. Armado con algunas estadísticas básicas, sabes que puedes realizar unas cuantas pruebas sencillas para saber si el nuevo correo electrónico de marketing era estadísticamente significativo o no. Antes de meterme demasiado en la maleza, establezcamos la hipótesis y determinemos el nivel de significación para la prueba.
Establecer la prueba de hipótesis
Lo primero que tienes que hacer en esta situación es establecer una prueba de hipótesis. En una prueba de hipótesis estándar, estableces las dos hipótesis: nula y alternativa. Para este ejemplo, la hipótesis será la siguiente:
- Hipótesis nula
-
El nuevo correo electrónico de marketing no es estadísticamente significativo; por tanto, las conversiones por correo electrónico seguirán siendo las mismas de media que el original.
- Hipótesis alternativa
-
El nuevo correo electrónico de marketing es estadísticamente significativo; por lo tanto, las conversiones por correo electrónico serán mayores de media que las del original.
Para demostrar la significación estadística, buscaré un valor p inferior a 0,05, que es mi nivel de significación.
En estadística, es importante comprender que siempre intentas validar tus supuestos utilizando las matemáticas. ¿Qué quiero decir con esto? Siempre quieres suponer que los resultados no van a cambiar cuando se introduzcan cosas nuevas. Por tanto, quieres suponer que la hipótesis nula es correcta, y tu prueba determinará si es errónea. En estadística, dirías que no has rechazado la hipótesis nula si el valor p es mayor que tu nivel de significación predeterminado. Si el valor p es inferior al nivel de significación, entonces la prueba es estadísticamente significativa, y rechazarías la hipótesis nula a favor de la alternativa.
Prueba Chi-cuadrado
Ahora que has establecido tu hipótesis, es el momento de realizar un análisis estadístico. Con el ánimo de proporcionarte unos conocimientos básicos, he decidido ejecutar una sencilla prueba estadística denominada prueba de chi-cuadrado. Una prueba chi-cuadrado es una prueba estadística utilizada para determinar si existe una asociación significativa (o independencia) entre dos variables categóricas. Es especialmente útil cuando se trabaja con datos que pueden organizarse en una tabla de contingencia.
Esta es una gran opción para ejecutar en esta situación y muy accesible, incluso si eres nuevo en estadística. No tienes que tener ningún software especial ni saber ningún tipo de codificación para calcular esta prueba. Puedes hacerlo a mano, ejecutarlo en Excel o buscar una calculadora en Internet.
Para empezar, revisemos la tabla de contingencia y añadámosle totales. Como puedes ver en la Tabla 1-2, he añadido totales para cada columna, fila y una columna de total general.
| Correo electrónico original | Nuevo correo electrónico de marketing | Totales | |
|---|---|---|---|
| No conversiones | 727 | 117 | 844 |
| Conversiones | 23 | 8 | 31 |
| Totales | 750 | 125 | 875 |
Ahora tienes que calcular valores esperados(E) para cada una de las celdas de la tabla. La fórmula es muy fácil. Toma el total de la fila, multiplícalo por el total de la columna de cada celda y luego divídelo por el total general. Así, para la celda superior izquierda (correo electrónico original por no conversiones) tomarías 750 × 844 ÷ 875 = 723,43. Calcularé cada uno de los valores previstos en las celdas correspondientes de la Tabla 1-3.
| Correo electrónico original | Nuevo correo electrónico de marketing | Totales | |
|---|---|---|---|
| No conversiones | E11 (750 × 844) ÷ 875 = 723.43 | E12 (125 × 844) ÷ 875 = 120.57 | 844 |
| Conversiones | E21 (750 × 31) ÷ 875 = 26.57 | E22 (125 × 31) ÷ 875 = 4.43 | 31 |
| Totales | 750 | 125 | 875 |
Puedes ver que he añadido una sintaxis matemática para cada celda(E11, E12, E21 y E22). Esto se refiere al valor esperado para la celda en la fila x y la columna y. Así pues, E11 es el valor esperado en la fila 1/columna 1. E12 es el valor esperado en la fila 1/columna 2, y así sucesivamente. Seguiré utilizando expresiones matemáticas y sintaxis similares a ésta a lo largo del libro y te introduciré en la sintaxis matemática por el camino.
Con tus valores esperados calculados, tienes que terminar comparando esos valores con los valores observados. Este paso se expresa matemáticamente mediante la siguiente fórmula:
En pocas palabras, tienes que tomar el valor original menos el valor esperado que acabas de calcular, elevarlo al cuadrado y dividirlo por el valor esperado. Harás esto para cada celda y luego sumarás cada uno de los valores que obtengamos. Si miramos E11, tenemos el valor original de 727 menos el valor esperado de 723,43, que es igual a 3,57. Coge 3,57 y sácale el cuadrado, que es igual a 12,7449. Luego divídelo por el valor esperado. Así pues, 12,7449 ÷ 723,43 = 0,017617. Redondearé ese número a 0,018. Puedes seguirlo en la Tabla 1-4 para cada celda.
| Correo electrónico original | Nuevo correo electrónico de marketing | Totales | |
|---|---|---|---|
| No conversiones | (727 - 723.43)2 ÷ 723.43 = 0.018 | (117 - 120.57)2 ÷ 120.57 = 0.106 | 844 |
| Conversiones | (23 - 26.57)2 ÷ 26.57 = 0.48 | (8 - 4.43)2 ÷ 4.43 = 2.877 | 31 |
| Totales | 750 | 125 | 875 |
Ahora toma los valores que obtuviste en cada celda de la Tabla 1-4 y súmalos. Aquí tienes los valores que obtuvimos para cada celda:
E11 = 0.018
E12 = 0.106
E21 = 0.48
E22 = 2.877
X2= (0.018 + 0.106 + 0.48 + 2.877) = 3.481
Eso te da un valor observado X2de 3,481. La regla de decisión para una prueba ji-cuadrado es la siguiente: si el valor observado X2es mayor que el valor crítico X2, rechazas la hipótesis nula. Hasta ahora, he calculado el valor observado X2, pero necesito obtener el valor crítico X2. Recuerda que, para nuestra prueba de hipótesis, fijamos un nivel de significación de 0,05. Utilizando ese nivel de significación, puedes determinar el valor crítico de X2.
La mejor forma de encontrar el valor crítico es buscarlo en una tabla de distribución. Una tabla de distribución es un recurso que puedes encontrar en Internet y que consiste en una gran tabla de valores críticos precalculados para ti. Utilizando el nivel de significación de 0,05, encontré que el valor crítico de X2era 3,84.
Teniendo en cuenta que el valor observado frente al valor crítico 3,481 no es superior a 3,84, por tanto no rechazarías la hipótesis nula. En términos sencillos, esto significa que la prueba demostró que el nuevo correo electrónico de marketing no tuvo un aumento estadísticamente significativo de las conversiones. Puedes concluir que seguir adelante con esta nueva campaña de marketing por correo electrónico dará resultados similares a la original, por término medio.
Conclusiones extraídas del análisis estadístico
Elegí este ejemplo por dos razones: (1) se trata de un ejemplo común del mundo real que te proporciona una comprensión básica de la estadística y de cómo se utiliza, y (2) este ejemplo se acerca mucho a ser estadísticamente significativo. En estadística, una de las lecciones más importantes es comprender los datos y hacer algunas suposiciones.
En esta situación, puedo volver atrás y decir que los resultados no produjeron un aumento significativo de las conversiones. Sin embargo, los datos sugieren que hay una ligera mejora. Mi recomendación sería aplazar la contratación, volver a realizar la prueba el próximo trimestre y dividir el total de correos electrónicos enviados 50/50 frente a 75/25. Esto daría al equipo un mayor tamaño de muestra para volver a realizar el análisis. Después de todo, puedes suponer que, aunque la nueva campaña no dio resultados estadísticamente significativos que demostraran que aumentó las conversiones, los resultados sí sugirieron que el nuevo correo electrónico de marketing no perjudicó en modo alguno a las conversiones.
Por tanto, no siempre es tan blanco y negro como parece. A diferencia de las matemáticas tradicionales, cuando utilizas la estadística, tienes que ser capaz de pensar con originalidad y hacer nuevas recomendaciones después de un análisis.
Visualización de Datos y Estadística
Para terminar, existe una ventaja obvia de la visualización de datos cuando intentas encontrar una visión rápida en tus datos; en el ejemplo anterior, puedes ver el poder que puede tener el análisis estadístico a la hora de tomar decisiones. Sin embargo, al unirlos es donde realmente sacarás el máximo partido de cualquier herramienta o análisis analítico.
Quiero compartir un gran ejemplo para hacer ver la importancia de unir la visualización de datos con el análisis estadístico. En la Tabla 1-5, tengo cuatro resúmenes estadísticos de cuatro conjuntos de datos diferentes.
| Conjunto de datos 1 | Conjunto de datos 2 | Conjunto de datos 3 | Conjunto de datos 4 | |||||
|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | |
| Obs | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| Media | 9.00 | 7.50 | 9.00 | 7.50090 | 9.00 | 7.50 | 9.00 | 7.50 |
| SD | 3.16 | 1.94 | 3.16 | 1.94 | 3.16 | 1.94 | 3.16 | 1.94 |
| r | 0.82 | 0.82 | 0.82 | 0.82 | ||||
Aquí puedes ver algunos estadísticos, como la desviación típica, r, la media y el número de observaciones de cada conjunto de datos. Explicaré detalladamente cada uno de estos estadísticos en próximos capítulos; sin embargo, fíjate en que son los mismos en los cuatro conjuntos de datos. Si trazaras los conjuntos de datos y los visualizaras, como se muestra en la Figura 1-15, podrías ver claramente que cada conjunto de datos es muy diferente.
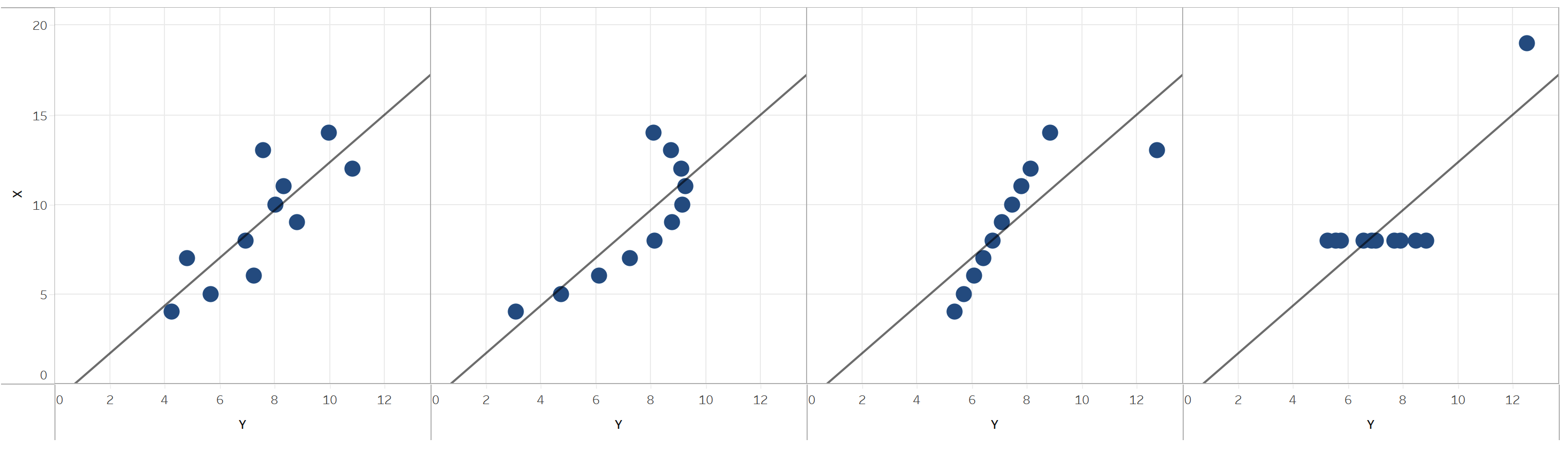
Figura 1-15. Representación visual del cuarteto de Anscombe
La Figura 1-15 es un ejemplo del cuarteto de Anscombe, y fue construido por el estadístico Francis Anscombe en 1973 para demostrar la importancia de visualizar tus datos antes y después de modelizarlos. Cuando construyes modelos estadísticos, necesitas visualizar los datos para comprender realmente cuál es la historia: si hay valores atípicos, correlación, normalización; la lista continúa. Por otra parte, la visualización de datos por sí sola deja muchas suposiciones y espacio para interpretaciones erróneas, por lo que necesitas respaldarla con estadísticas. El resto de este libro tratará precisamente de eso.
Resumen
En este capítulo he explicado qué es Tableau y he enumerado varios de sus productos clave. Luego he repasado algunos términos clave que utilizaré a lo largo del libro cuando te guíe por cada tutorial. Este conocimiento básico será clave en capítulos posteriores, especialmente si eres nuevo en Tableau.
A continuación, abordé algunas ideas y términos estadísticos fundamentales. Después, uní esos términos con un caso práctico. Para presentarte la idea de cómo se unen la estadística y la visualización de datos, te mostré el ejemplo del cuarteto de Anscombe.
En los capítulos siguientes, te mostraré cómo empezar a incorporar análisis estadísticos a tus visualizaciones de datos en Tableau. Aprenderás a visualizar la distribución de tus datos, detectar valores atípicos, predecir valores futuros, crear un análisis de conglomerados, utilizar la regresión para hacer predicciones y conectar con recursos externos para obtener modelos estadísticos más avanzados.
Si has llegado hasta aquí y todavía necesitas algo más de práctica básica, te recomiendo los siguientes libros para familiarizarte con Tableau Desktop y sus capacidades:
-
Tableau práctico por Ryan Sleeper (O'Reilly, 2018)
-
Libro de cocina de Tableau Desktop por Lorna Brown (O'Reilly, 2021)
-
Estrategias de Tableau por Ann Jackson y Luke Stanke (O'Reilly, 2021)
1 Véase el artículo del blog de David Kirkpatrick sobre la conversión, "Marketing 101: ¿Qué es la conversión?", MarketingSherpa, 15 de marzo de 2021.
Get Cuadro estadístico now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.