Computing for Numerical Methods Using Visual C++

Chapter 5. Systems of Linear Equations

• 5.1 Introduction

• 5.2 Existence of Solutions

• 5.3 Gaussian Elimination Techniques

• 5.4 LU Factorization Methods

• 5.5 Iterative Techniques

• 5.6 Visualizing the Solution: Code5

• 5.7 Summary

  • Numerical Exercises

  • Programming Challenges

INTRODUCTION

A linear system consists of a set of equations with some governing parameters or variables that control the system. The variables that make up the system can be stated in the form of differential equations or autonomous variables. The system works in a dependent manner where changes in one or more variables affect the performance of the whole system in general.

Definition 5.1. An equation in the following form with the unknowns x_i and constants a_i, for i = 1, 2, ..., n, is said to be a linear equation:

Equation 5.1. 

In this definition, each unknown x_i must have an index power of 1. Also, a linear equation cannot have a variable inside sine, cosine, tangent, exponent, logarithm, and other operators. It follows that any equation in the form other than Equation (5.1) is called a nonlinear equation.

The following equations are examples of linear equations:

Equation 5.2. 

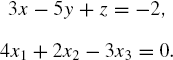
A system of linear equations consists of a set of linear equations and a set of unknowns. In general, a system of linear equations with m equations and n unknowns ...