C++程序设计：原理与实践（进阶篇）（原书第2版）

18.8　Polygon

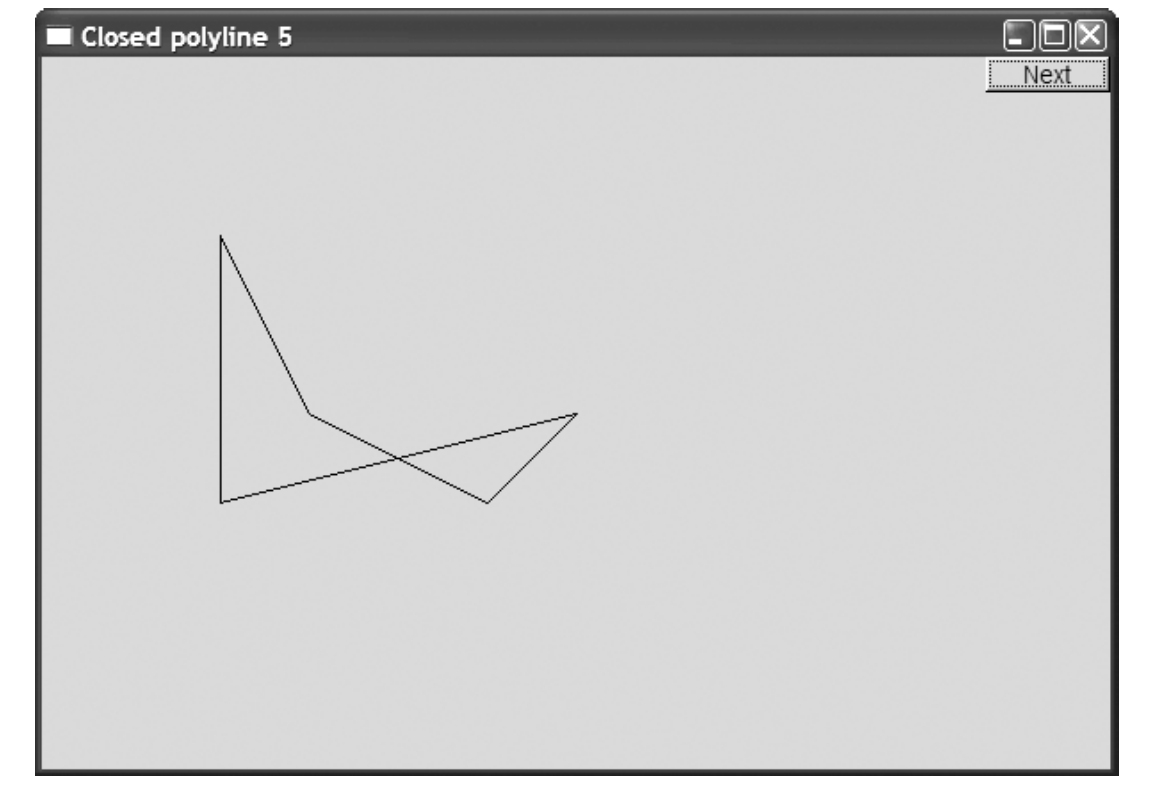
Polygon与Closed_polyline非常相似，唯一的区别是Polygon不允许出现交叉的线。例如：18.7节中的Closed_polyline是一个多边形，但如果再添加一个点：

运行结果为：

根据经典几何定义，这个Closed_polyline就不是多边形了。那么，如何定义Polygon才能正确利用与Closed_polyline之间的关系，又不违反几何规则？前文中有一个明显的暗示：Polygon是不存在交叉线的Closed_polygon。换句话说，我们就可以强调由点建立形状的过程，如果新添加的Point定义的线段不与Polygon任何现有的线相交时，这样的Closed_polyline就是Polygon。

由此可定义Polygon如下：

我们在这里继承了Closed_polyline中draw_lines（）函数的定义，这不但节省了工作量，还避免了重复代码。不幸的是，每次调用add（）时，我们都需要检查是否有线段交叉。这导致一个低效的（平方阶的）算法——定义一个N个点构成的Polygon时，需调用N（N-1）/2次intersect（）函数，因此算法的时间复杂度为N的平方阶。在实际应用中，我们假设Polygon类只用于顶点数比较少的多边形。例如，创建一个24个Point的Polygon需要调用intersect（）函数24×（24-1）/2==276次，这还是可以接受的，但如果创建2000个顶点构成的多边形则需要大约2000000次函数调用，这时可能需要寻找更优的算法，接口可能也需要相应修改。 ...