20.1 Fundamental Trigonometric Identities

  • Trigonometric Identities • Basic Identities • Proving Trigonometric Identities

From the definitions in Chapters 4 and 8, recall that sin θ = y  / r and csc θ = r / y (see Fig. 20.1). Because y / r = 1 / (r / y) ,  we see that sin θ = 1 / csc θ .  These definitions hold for any angle, which means that sin θ = 1 / csc θ is true for any angle. This type of relation, which is true for any value of the variable, is called an identity. Of course, values where division by zero would be indicated are excluded.

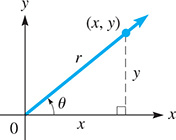
A ray of length r rises from (0, 0) and through (x, y) at angle theta to the x-axis. Dashed segment y falls from (x, y) and meets the x-axis at a right angle. From here back to the origin is x.

Fig. 20.1

In this section, we develop several important identities involving the trigonometric ...

Get Basic Technical Mathematics, 11th Edition now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial