Kapitel 1. Maschinelles Lernen
Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: translation-feedback@oreilly.com
Maschinelles Lernen erweitert die Grenzen des Möglichen, indem es Computern ermöglicht, Probleme zu lösen, die noch vor wenigen Jahren unlösbar waren. Von der Erkennung von Betrug und medizinischen Diagnosen bis hin zu Produktempfehlungen und Autos, die "sehen", was vor ihnen liegt - maschinelles Lernen beeinflusst unser Leben jeden Tag. Während du dies liest, nutzen Wissenschaftler/innen maschinelles Lernen, um die Geheimnisse des menschlichen Genoms zu entschlüsseln. Wenn wir eines Tages Krebs heilen, werden wir dem maschinellen Lernen dafür danken, dass es möglich wurde.
Maschinelles Lernen ist revolutionär, weil es eine Alternative zur algorithmischen Problemlösung bietet. Mit einem Rezept oder Algorithmus ist es nicht schwer, eine App zu schreiben, die ein Passwort verschlüsselt oder eine monatliche Hypothekenzahlung berechnet. Du programmierst den Algorithmus, gibst ihn ein und erhältst das Ergebnis zurück. Etwas ganz anderes ist es, einen Code zu schreiben, der bestimmt, ob auf einem Foto eine Katze oder ein Hund zu sehen ist. Du kannst versuchen, es algorithmisch zu machen, aber sobald du es hinbekommst, wirst du auf ein Katzen- oder Hundefoto stoßen, das den Algorithmus durchbricht.
Das maschinelle Lernen verfolgt einen anderen Ansatz, um Eingaben in Ausgaben zu verwandeln. Anstatt sich darauf zu verlassen, dass du einen Algorithmus implementierst, untersucht er einen Datensatz mit Eingaben und Ausgaben und lernt in einem Prozess, der als Training bezeichnet wird, wie er selbst Ausgaben erzeugt. Unter der Haube passen spezielle Algorithmen, die sogenannten Lernalgorithmen, mathematische Modelle an die Daten an und kodieren die Beziehung zwischen eingehenden und ausgehenden Daten. Einmal trainiert, kann ein Modell neue Eingaben akzeptieren und Ausgaben erzeugen, die mit denen der Trainingsdaten übereinstimmen.
Um mit maschinellem Lernen zwischen Katzen und Hunden zu unterscheiden, programmierst du keinen Katze-gegen-Hund-Algorithmus. Stattdessen trainierst du ein maschinelles Lernmodell mit Katzen- und Hundefotos. Der Erfolg hängt von dem verwendeten Lernalgorithmus sowie von der Qualität und Menge der Trainingsdaten ab.
Ein Teil der Ausbildung zum Ingenieur für maschinelles Lernen besteht darin, sich mit den verschiedenen Lernalgorithmen vertraut zu machen und ein Gespür dafür zu entwickeln, wann ein Algorithmus im Vergleich zu einem anderen eingesetzt werden sollte. Dieses Gespür entsteht durch Erfahrung und durch das Verständnis dafür, wie maschinelles Lernen mathematische Modelle auf Daten anpasst. Dieses Kapitel ist der erste Schritt auf dieser Reise. Es beginnt mit einem Überblick über maschinelles Lernen und die gebräuchlichsten Arten von maschinellen Lernmodellen und schließt mit der Vorstellung von zwei beliebten Lernalgorithmen und deren Anwendung zur Erstellung einfacher, aber voll funktionsfähiger Modelle.
Was ist maschinelles Lernen?
Auf einer existentiellen Ebene ist maschinelles Lernen (ML) ein Mittel, um Muster in Zahlen zu finden und diese Muster für Vorhersagen zu nutzen. ML ermöglicht es, ein Modell mit Reihen oder Sequenzen von 1en und 0en zu trainieren und aus den Daten zu lernen, sodass das Modell bei einer neuen Sequenz vorhersagen kann, wie das Ergebnis aussehen wird. Lernen ist der Prozess, durch den ML Muster findet, die zur Vorhersage zukünftiger Ergebnisse verwendet werden können.
Betrachte zum Beispiel die in Abbildung 1-1 dargestellte Tabelle mit 1en und 0en. Jede Zahl in der vierten Spalte basiert irgendwie auf den drei Zahlen, die ihr in der gleichen Zeile vorausgehen. Was ist die fehlende Zahl?
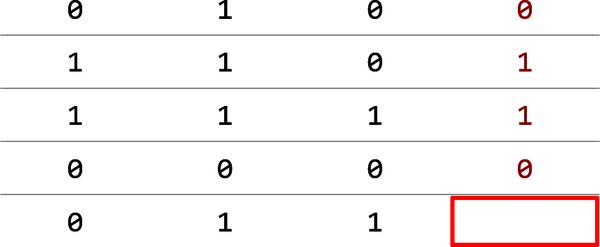
Abbildung 1-1. Einfacher Datensatz bestehend aus 0s und 1s
Eine mögliche Lösung ist, dass für eine bestimmte Zeile, wenn die ersten drei Spalten mehr 0en als 1en enthalten, die vierte eine 0 enthält. Wenn die ersten drei Spalten mehr 1en als 0en enthalten, ist die Antwort eine 1. Nach dieser Logik sollte das leere Feld eine 1 enthalten. Datenwissenschaftler bezeichnen die Spalte mit den Antworten (die rote Spalte in der Abbildung) als Label-Spalte. Die übrigen Spalten sind die Merkmalsspalten. Das Ziel eines Vorhersagemodells ist es, Muster in den Zeilen der Merkmalsspalten zu finden, die eine Vorhersage des Labels ermöglichen.
Wenn alle Datensätze so einfach wären, bräuchte man kein maschinelles Lernen. Aber in der Realität sind die Datensätze größer und komplexer. Was wäre, wenn der Datensatz Millionen von Zeilen und Tausende von Spalten enthielte, wie es beim maschinellen Lernen häufig der Fall ist? Und was wäre, wenn der Datensatz dem in Abbildung 1-2 ähneln würde?

Abbildung 1-2. Ein komplexerer Datensatz
Es ist schwierig für einen Menschen, diesen Datensatz zu untersuchen und eine Reihe von Regeln aufzustellen, um vorherzusagen, ob das rote Kästchen eine 0 oder eine 1 enthält. (Und nein, es ist nicht so einfach, wie 1en und 0en zu zählen.) Stell dir vor, wie viel schwieriger es wäre, wenn der Datensatz wirklich Millionen von Zeilen und Tausende von Spalten hätte.
Das ist es, worum es beim maschinellen Lernen geht: Muster in riesigen Datensätzen mit Zahlen zu finden. Dabei spielt es keine Rolle, ob es 100 Zeilen oder 1.000.000 Zeilen sind. In vielen Fällen ist mehr besser, denn 100 Zeilen bieten vielleicht nicht genug Stichproben, um Muster zu erkennen.
Es ist keine grobe Vereinfachung zu sagen, dass maschinelles Lernen Probleme löst, indem es Muster in Zahlenmengen mathematisch modelliert. Fast jedes Problem lässt sich auf eine Reihe von Zahlen reduzieren. Eine der häufigsten Anwendungen für maschinelles Lernen ist zum Beispiel die Stimmungsanalyse: Man betrachtet ein Textbeispiel wie eine Filmkritik oder einen Kommentar auf einer Website und ordnet ihm eine 0 für eine negative Stimmung zu (z. B. "Das Essen war fade und der Service schrecklich.") oder eine 1 für eine positive Stimmung ("Hervorragendes Essen und hervorragender Service. Ich kann es kaum erwarten, wiederzukommen!"). Manche Bewertungen können gemischt sein, wie z.B. "Der Burger war toll, aber die Pommes waren matschig", daher verwenden wir die Wahrscheinlichkeit, dass die Bewertung eine 1 ist, als Stimmungswert. Ein sehr negativer Kommentar könnte mit 0,1 bewertet werden, während ein sehr positiver Kommentar mit 0,9 bewertet werden könnte, d.h. es besteht eine 90%ige Chance, dass er eine positive Stimmung ausdrückt.
Sentiment-Analysatoren und andere Modelle, die mit Text arbeiten, werden häufig auf Datensätzen wie dem in Abbildung 1-3 trainiert, der eine Zeile für jede Textprobe und eine Spalte für jedes Wort im Textkorpus (alle Wörter im Datensatz) enthält. Ein typischer Datensatz wie dieser kann Millionen von Zeilen und 20.000 oder mehr Spalten enthalten. Jede Zeile enthält in der Label-Spalte eine 0 für negative Stimmung oder eine 1 für positive Stimmung. In jeder Zeile steht die Anzahl der Wörter - wie oft ein bestimmtes Wort in einer einzelnen Probe vorkommt. Der Datensatz ist spärlich, d.h. er besteht hauptsächlich aus 0en und gelegentlich aus einer Zahl ungleich Null. Aber maschinelles Lernen kümmert sich nicht um die Zusammensetzung der Zahlen. Wenn es Muster gibt, die ausgenutzt werden können, um festzustellen, ob die nächste Probe eine positive oder negative Stimmung ausdrückt, wird es sie finden. Spamfilter verwenden solche Datensätze mit 1en und 0en in der Label-Spalte, die Spam- und Nicht-Spam-Nachrichten kennzeichnen. Dadurch erreichen moderne Spamfilter einen erstaunlichen Grad an Genauigkeit. Außerdem werden diese Modelle mit der Zeit immer intelligenter, da sie mit immer mehr E-Mails trainiert werden.
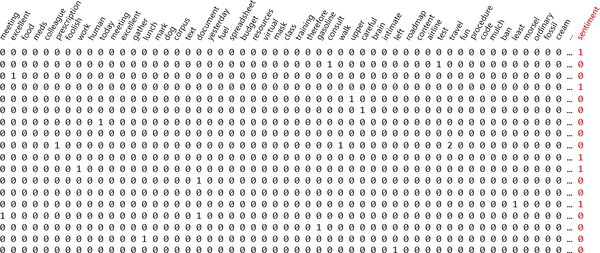
Abbildung 1-3. Datensatz für die Stimmungsanalyse
Die Sentiment-Analyse ist ein Beispiel für eine Textklassifizierungsaufgabe: Sie analysiert eine Textprobe und klassifiziert sie als positiv oder negativ. Maschinelles Lernen hat sich auch bei der Bildklassifizierung bewährt. Ein einfaches Beispiel für die Bildklassifizierung ist die Betrachtung von Katzen- und Hundefotos und die Einstufung jedes einzelnen als Katzenbild (0) oder Hundebild (1). In der realen Welt werden Bilder klassifiziert, um z. B. defekte Teile am Fließband zu kennzeichnen, Objekte im Blickfeld eines selbstfahrenden Autos zu identifizieren und Gesichter auf Fotos zu erkennen.
Klassifizierungsmodelle für Bilder werden mit Datensätzen wie in Abbildung 1-4 trainiert, in denen jede Zeile ein Bild und jede Spalte einen Pixelwert enthält. Ein Datensatz mit 1.000.000 Bildern, die 200 Pixel breit und 200 Pixel hoch sind, enthält 1.000.000 Zeilen und 40.000 Spalten. Das sind insgesamt 40 Milliarden Zahlen, oder 120.000.000.000, wenn es sich um Farbbilder und nicht um Graustufenbilder handelt. (Bei Farbbildern bestehen die Pixelwerte aus drei Zahlen und nicht aus einer.) Die Spalte "Label" enthält eine Zahl, die die Klasse oder Kategorie angibt, zu der das entsprechende Bild gehört - in diesem Fall die Person, deren Gesicht auf dem Bild zu sehen ist: 0 für Gerhard Schröder, 1 für George W. Bush, und so weiter.

Abbildung 1-4. Datensatz für die Bildklassifizierung
Diese Gesichtsbilder stammen aus einem berühmten öffentlichen Datensatz namens Labeled Faces in the Wild, kurz LFW. Er ist einer von unzähligen beschrifteten Datensätzen, die an verschiedenen Stellen für die Öffentlichkeit veröffentlicht werden. Maschinelles Lernen ist nicht schwer, wenn du mit beschrifteten Datensätzen arbeiten kannst - Datensätze, die andere (oft Studierende) in mühevoller Arbeit mit 1en und 0en beschriftet haben. In der realen Welt verbringen Ingenieure manchmal den Großteil ihrer Zeit mit der Erstellung dieser Datensätze. Eines der beliebtesten Repositories für öffentliche Datensätze ist Kaggle.com, das viele nützliche Datensätze zur Verfügung stellt und Wettbewerbe veranstaltet, bei denen angehende ML-Praktiker ihre Fähigkeiten testen können.
Maschinelles Lernen vs. Künstliche Intelligenz
Die Begriffe maschinelles Lernen und künstliche Intelligenz (KI) werden heute fast austauschbar verwendet, aber tatsächlich hat jeder Begriff eine spezifische Bedeutung, wie in Abbildung 1-5 dargestellt.
Technisch gesehen ist maschinelles Lernen ein Teilbereich der KI, der nicht nur Modelle des maschinellen Lernens umfasst, sondern auch andere Arten von Modellen wie Expertensysteme (Systeme, die Entscheidungen auf der Grundlage von selbst definierten Regeln treffen) und Systeme des verstärkenden Lernens, die Verhaltensweisen lernen, indem sie positive Ergebnisse belohnen und negative bestrafen. Ein Beispiel für ein System mit Verstärkungslernen ist AlphaGo, das erste Computerprogramm, das einen menschlichen Profi-Go-Spieler besiegt hat. Es trainiert mit bereits gespielten Partien und lernt selbstständig Strategien zum Gewinnen.
In der Praxis ist das, was die meisten Menschen heute als KI bezeichnen, in Wirklichkeit Deep Learning, eine Untergruppe des maschinellen Lernens. Deep Learning ist maschinelles Lernen, das mit neuronalen Netzwerken durchgeführt wird. (Es gibt Formen des Deep Learning, die keine neuronalen Netze verwenden - Deep-Boltzmann-Maschinen sind ein Beispiel dafür -, aber die überwiegende Mehrheit des Deep Learning verwendet heute neuronale Netze.) ML-Modelle können also in konventionelle Modelle, die Lernalgorithmen verwenden, um Muster in Daten zu modellieren, und in Deep-Learning-Modelle, die dazu neuronale Netze verwenden, unterteilt werden.
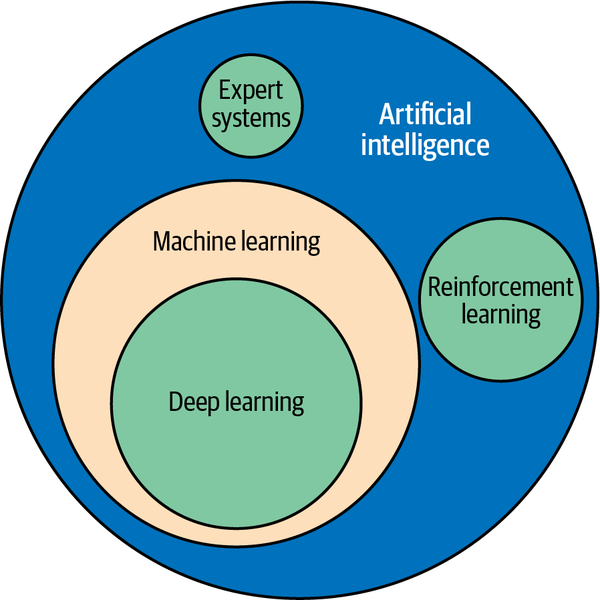
Abbildung 1-5. Beziehung zwischen maschinellem Lernen, Deep Learning und KI
Im Laufe der Zeit haben Datenwissenschaftler/innen spezielle Arten von neuronalen Netzen entwickelt, die sich für bestimmte Aufgaben eignen, z. B. für Aufgaben, die mit Computer Vision zu tun haben - z. B. das Herausfiltern von Informationen aus Bildern - oder für Aufgaben, die mit menschlichen Sprachen zu tun haben, z. B. das Übersetzen von Englisch ins Französische. Ab Kapitel 8 tauchen wir tief in die Welt der neuronalen Netze ein und du erfährst, wie Deep Learning das maschinelle Lernen auf ein neues Niveau gehoben hat.
Überwachtes vs. unüberwachtes Lernen
Die meisten ML-Modelle lassen sich in zwei große Kategorien einteilen: überwachte Lernmodelle und unüberwachte Lernmodelle. Der Zweck von überwachten Lernmodellen ist es, Vorhersagen zu treffen. Du trainierst sie mit gekennzeichneten Daten, damit sie zukünftige Eingaben annehmen und vorhersagen können, wie die Kennzeichnungen lauten werden. Die meisten ML-Modelle, die heute verwendet werden, sind überwachte Lernmodelle. Ein gutes Beispiel ist das Modell, mit dem die US-Post handgeschriebene Postleitzahlen in Ziffern umwandelt, die ein Computer erkennen kann, um die Post zu sortieren. Ein anderes Beispiel ist das Modell, das dein Kreditkartenunternehmen verwendet, um Einkäufe zu autorisieren .
Unüberwachte Lernmodelle hingegen benötigen keine markierten Daten. Ihr Zweck ist es, Einblicke in bestehende Daten zu geben oder Daten in Kategorien zu gruppieren und zukünftige Eingaben entsprechend zu kategorisieren. Ein klassisches Beispiel für unüberwachtes Lernen ist die Untersuchung von Datensätzen über die von deinem Unternehmen gekauften Produkte und die Kunden, die sie gekauft haben, um herauszufinden, welche Kunden am meisten an einem neuen Produkt interessiert sind, das du auf den Markt bringen willst.
Ein Spam-Filter ist ein überwachtes Lernmodell. Es benötigt beschriftete Daten. Ein Modell, das Kunden anhand ihres Einkommens, ihrer Kreditwürdigkeit und ihrer Kaufhistorie segmentiert, ist ein unbeaufsichtigtes Lernmodell, und die Daten, die es benötigt, müssen nicht beschriftet sein. Um den Unterschied zu verdeutlichen, wird in diesem Kapitel näher auf das überwachte und das unüberwachte Lernen eingegangen.
Unüberwachtes Lernen mit k-Means Clustering
Beim unüberwachten Lernen wird häufig eine Technik namens Clustering eingesetzt. Der Zweck des Clusterns ist es, Daten nach Ähnlichkeit zu gruppieren. Der bekannteste Clustering-Algorithmus ist das k-means Clustering, bei dem n Datenproben in m Cluster eingeteilt werden, wobei m eine von dir festgelegte Zahl ist.
Die Gruppierung erfolgt durch einen iterativen Prozess, bei dem ein Schwerpunkt für jedes Cluster berechnet wird und die Proben anhand ihrer Nähe zu den Clusterschwerpunkten den Clustern zugeordnet werden. Wenn der Abstand zwischen einer bestimmten Probe und dem Schwerpunkt von Cluster 1 2,0 und der Abstand zwischen derselben Probe und dem Mittelpunkt von Cluster 2 3,0 beträgt, wird die Probe Cluster 1 zugeordnet. In Abbildung 1-6 sind 200 Proben locker in drei Clustern angeordnet. Das Diagramm auf der linken Seite zeigt die rohen, nicht gruppierten Proben. Das Diagramm auf der rechten Seite zeigt die Clusterschwerpunkte (die roten Punkte) mit den nach Clustern gefärbten Proben.
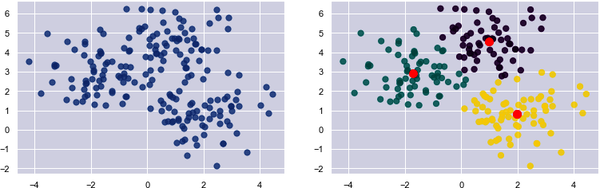
Abbildung 1-6. Mit k-means Clustering gruppierte Datenpunkte
Wie programmierst du ein unüberwachtes Lernmodell, das die k-means-Clustering-Funktion nutzt? Am einfachsten ist es, wenn du die weltweit beliebteste Bibliothek für maschinelles Lernen verwendest: Scikit-Learn. Sie ist kostenlos, quelloffen und in Python geschrieben. Die Dokumentation ist großartig, und wenn du eine Frage hast, findest du wahrscheinlich eine Antwort, wenn du sie googelst. Ich werde Scikit für die meisten Beispiele in der ersten Hälfte dieses Buches verwenden. Im Vorwort des Buches wird beschrieben, wie du Scikit installierst und deinen Computer so konfigurierst, dass meine Beispiele ausgeführt werden können (oder wie du einen Docker-Container dafür verwendest).
Um dich mit dem k-means Clustering vertraut zu machen, erstelle ein neues Jupyter-Notebook und füge die folgenden Anweisungen in die erste Zelle ein:
%matplotlibinlineimportmatplotlib.pyplotaspltimportseabornassnssns.set()
Führe in dieser Zelle aus und führe dann den folgenden Code in der nächsten Zelle aus, um eine halbzufällige Auswahl von x- und y-Koordinatenpaaren zu erzeugen. Dieser Code verwendet die Funktionmake_blobs von Scikit, um die Koordinatenpaare zu erzeugen, und die Funktionscatter von Matplotlib, um sie darzustellen:
fromsklearn.datasetsimportmake_blobspoints,cluster_indexes=make_blobs(n_samples=300,centers=4,cluster_std=0.8,random_state=0)x=points[:,0]y=points[:,1]plt.scatter(x,y,s=50,alpha=0.7)
Deine Ausgabe sollte mit meiner identisch sein, dank des random_state Parameters, der den Zufallszahlengenerator, der intern von make_blobs verwendet wird, seedet:
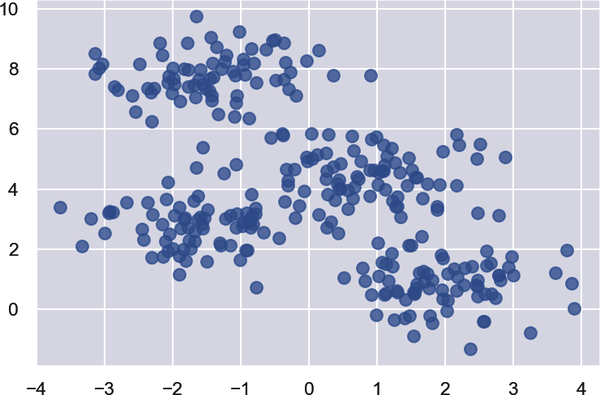
Als Nächstes, benutze das k-means Clustering, um die Koordinatenpaare in vier Gruppen zu unterteilen. Anschließend werden die Zentren der Cluster in rot dargestellt und die Datenpunkte nach Clustern farblich gekennzeichnet. Die KlasseKMeans von Scikit übernimmt die schwere Arbeit. Sobald sie an die Koordinatenpaare angepasst ist, kannst du die Positionen der Zentren unter KMeans' cluster_centers_ Attribut:
fromsklearn.clusterimportKMeanskmeans=KMeans(n_clusters=4,random_state=0)kmeans.fit(points)predicted_cluster_indexes=kmeans.predict(points)plt.scatter(x,y,c=predicted_cluster_indexes,s=50,alpha=0.7,cmap='viridis')centers=kmeans.cluster_centers_plt.scatter(centers[:,0],centers[:,1],c='red',s=100)
Hier ist das Ergebnis:

Versuche, n_clusters auf andere Werte wie 3 und 5 zu setzen, um zu sehen, wie die Punkte mit unterschiedlichen Clusterzahlen gruppiert werden. Das wirft die Frage auf: Woher weißt du, welche Anzahl von Clustern die richtige ist? Die Antwort ist nicht immer offensichtlich, wenn du dir eine Grafik ansiehst, und wenn die Daten mehr als drei Dimensionen haben, kannst du sie sowieso nicht grafisch darstellen.
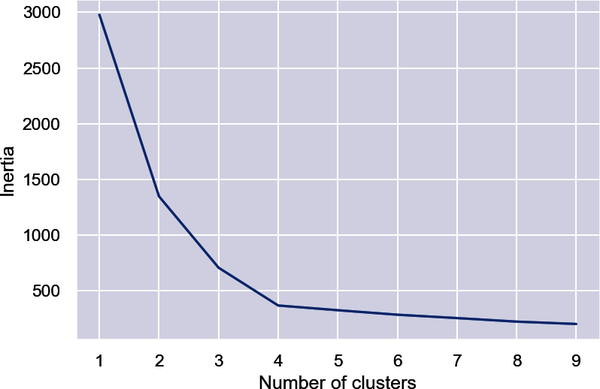
Eine Möglichkeit, die richtige Zahl zu ermitteln, ist die Ellbogenmethode, bei der die Inertien (die Summe der quadrierten Abstände der Datenpunkte zum nächsten Clusterzentrum) aus KMeans.inertia_ als Funktion der Clusteranzahl dargestellt werden. Zeichne die Inertien auf diese Weise auf und suche nach dem schärfsten Knick in der Kurve:
inertias=[]foriinrange(1,10):kmeans=KMeans(n_clusters=i,random_state=0)kmeans.fit(points)inertias.append(kmeans.inertia_)plt.plot(range(1,10),inertias)plt.xlabel('Number of clusters')plt.ylabel('Inertia')
In diesem Beispiel scheint es, dass 4 die richtige Anzahl von Clustern ist:
Im wirklichen Leben ist der Ellbogen vielleicht nicht so eindeutig. Das ist in Ordnung, denn wenn du die Daten auf verschiedene Arten gruppierst, erhältst du manchmal Erkenntnisse, die du sonst nicht erhalten würdest .
Anwendung von k-Means Clustering auf Kundendaten
Verwenden wir das k-means Clustering, um ein echtes Problem zu lösen: die Segmentierung von Kunden, um diejenigen zu identifizieren, die mit einer Werbeaktion angesprochen werden sollen, um ihre Kaufaktivität zu erhöhen. Als Datensatz verwendest du einen Beispiel-Datensatz zur Kundensegmentierung mit dem Namen customers.csv. Beginne mit, indem du in dem Ordner, in dem sich deine Notizbücher befinden, ein Unterverzeichnis mit dem Namen Data erstellst, customers.csv herunterlädst und in das Unterverzeichnis Data kopierst. Benutze dann den folgenden Code, um den Datensatz in ein Pandas DataFrame zu laden und die ersten fünf Zeilen anzuzeigen:
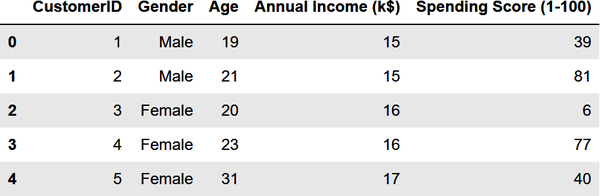
importpandasaspdcustomers=pd.read_csv('Data/customers.csv')customers.head()
Aus der Ausgabe erfährst du, dass der Datensatz fünf Spalten enthält, von denen zwei das Jahreseinkommen und den Ausgabenwert des Kunden beschreiben. Letzteres ist ein Wert zwischen 0 und 100. Je höher die Zahl, desto mehr hat der Kunde in der Vergangenheit bei deinem Unternehmen ausgegeben:
Verwende nun den folgenden Code, um die Jahreseinkommen und die Ausgabenwerte darzustellen:
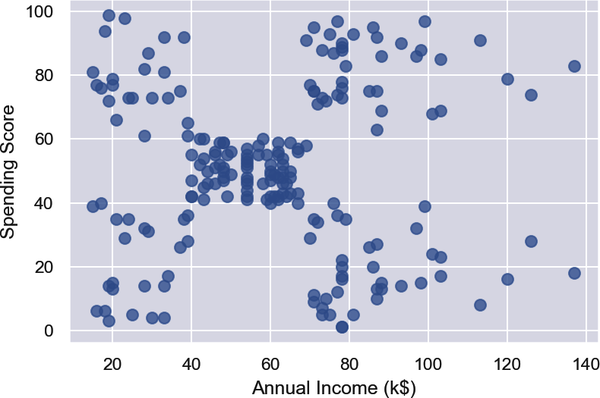
%matplotlibinlineimportmatplotlib.pyplotaspltimportseabornassnssns.set()points=customers.iloc[:,3:5].valuesx=points[:,0]y=points[:,1]plt.scatter(x,y,s=50,alpha=0.7)plt.xlabel('Annual Income (k$)')plt.ylabel('Spending Score')
Aus den Ergebnissen geht hervor, dass die Datenpunkte ungefähr in fünf Cluster fallen:
Verwende den folgenden Code, um die Kunden in fünf Cluster zu unterteilen und die Cluster hervorzuheben:
fromsklearn.clusterimportKMeanskmeans=KMeans(n_clusters=5,random_state=0)kmeans.fit(points)predicted_cluster_indexes=kmeans.predict(points)plt.scatter(x,y,c=predicted_cluster_indexes,s=50,alpha=0.7,cmap='viridis')plt.xlabel('Annual Income (k$)')plt.ylabel('Spending Score')centers=kmeans.cluster_centers_plt.scatter(centers[:,0],centers[:,1],c='red',s=100)
Hier ist das Ergebnis:
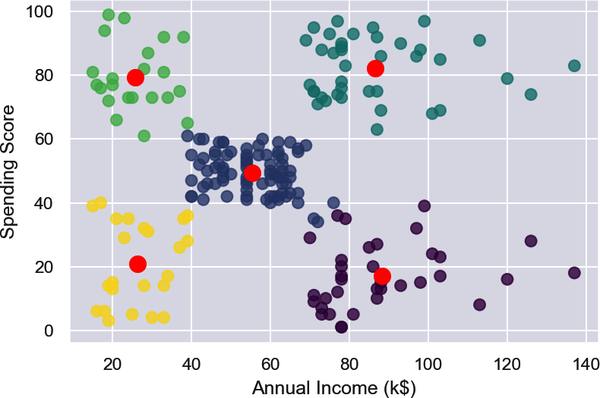
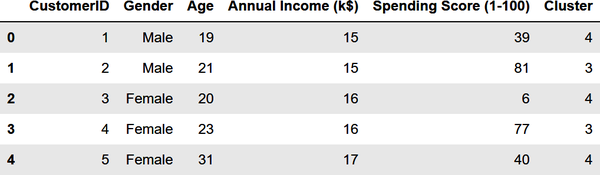
Die Kunden im unteren rechten Quadranten des Diagramms sind möglicherweise gut geeignet, um ihre Ausgaben mit einer Werbeaktion zu erhöhen. Warum? Weil sie ein hohes Einkommen, aber niedrige Ausgabenwerte haben. Verwende die folgenden Anweisungen, um eine Kopie von DataFrame zu erstellen und eine Spalte mit dem Namen Cluster hinzuzufügen, die Cluster-Indizes enthält:
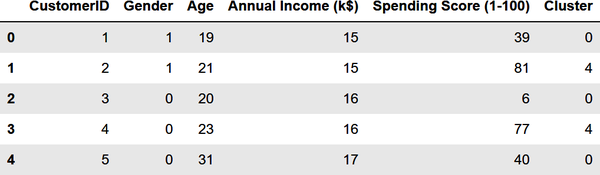
df=customers.copy()df['Cluster']=kmeans.predict(points)df.head()
Hier ist die Ausgabe:
Verwende nun den folgenden Code, um die IDs der Kunden auszugeben, die ein hohes Einkommen, aber eine niedrige Ausgabenquote haben:
importnumpyasnp# Get the cluster index for a customer with a high income and low spending scorecluster=kmeans.predict(np.array([[120,20]]))[0]# Filter the DataFrame to include only customers in that clusterclustered_df=df[df['Cluster']==cluster]# Show the customer IDsclustered_df['CustomerID'].values
Du kannst die resultierenden Kunden-IDs ganz einfach verwenden, um Namen und E-Mail-Adressen aus einer Kundendatenbank zu extrahieren:
array([125,129,131,135,137,139,141,145,147,149,151,153,155,157,159,161,163,165,167,169,171,173,175,177,179,181,183,185,187,189,191,193,195,197,199],dtype=int64)
Das Wichtigste dabei ist, dass du die Kunden mit Hilfe der Clusterbildung nach Jahreseinkommen und Ausgabenhöhe gruppiert hast. Sobald die Kunden auf diese Weise gruppiert sind, ist es ein Leichtes, die Kunden in den einzelnen Clustern aufzuzählen.
Kunden anhand von mehr als zwei Dimensionen segmentieren
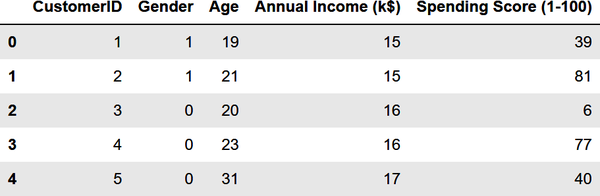
Das vorherige Beispiel war einfach, weil du nur zwei Variablen verwendet hast: Jahreseinkommen und Ausgabenwerte. Das hättest du auch ohne die Hilfe des maschinellen Lernens machen können. Aber jetzt wollen wir die Kunden noch einmal segmentieren, diesmal mit allem außer den Kunden-IDs. Beginne damit, die Zeichenfolgen "Male" und "Female" in der Spalte Gender durch 1en und 0en zu ersetzen, ein Prozess, der als Label Encoding bekannt ist. Dies ist notwendig, weil maschinelles Lernen nur mit numerischen Daten umgehen kann:
fromsklearn.preprocessingimportLabelEncoderdf=customers.copy()encoder=LabelEncoder()df['Gender']=encoder.fit_transform(df['Gender'])df.head()
Die Spalte Gender enthält jetzt 1en und 0en:
Extrahiere die Spalten Geschlecht, Alter, Jahreseinkommen und Ausgabenpunkte. Bestimme dann mit der Ellbogenmethode die optimale Anzahl von Clustern auf der Grundlage dieser Merkmale:
points=df.iloc[:,1:5].valuesinertias=[]foriinrange(1,10):kmeans=KMeans(n_clusters=i,random_state=0)kmeans.fit(points)inertias.append(kmeans.inertia_)plt.plot(range(1,10),inertias)plt.xlabel('Number of Clusters')plt.ylabel('Inertia')
Der Ellbogen ist dieses Mal weniger deutlich, aber 5 scheint eine vernünftige Zahl zu sein:
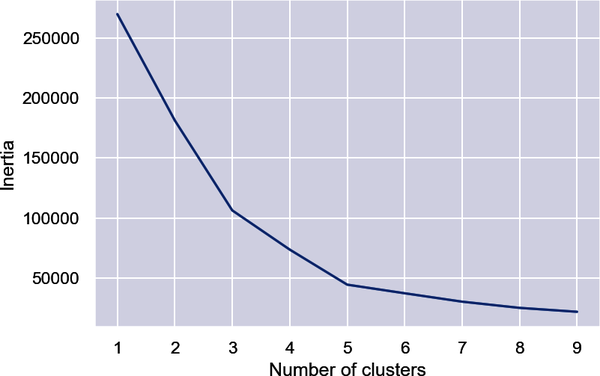
Unterteile die Kunden in fünf Cluster und füge eine Spalte namens Cluster hinzu, die den Index des Clusters (0-4) enthält, dem der Kunde zugeordnet wurde:
kmeans=KMeans(n_clusters=5,random_state=0)kmeans.fit(points)df['Cluster']=kmeans.predict(points)df.head()
Hier ist die Ausgabe:
Du hast für jeden Kunden eine Clusternummer, aber was bedeutet sie? Du kannst Geschlecht, Alter, Jahreseinkommen und Ausgabenniveau nicht in einem zweidimensionalen Diagramm darstellen, so wie du es im vorherigen Beispiel mit dem Jahreseinkommen und dem Ausgabenniveau getan hast. Aber du kannst den Mittelwert (Durchschnitt) dieser Werte für jedes Cluster anhand der Clusterschwerpunkte ermitteln. Erstelle eine neue DataFrame mit Spalten für das Durchschnittsalter, das Durchschnittseinkommen usw. und zeige die Ergebnisse dann in einer Tabelle:
results=pd.DataFrame(columns=['Cluster','Average Age','Average Income','Average Spending Index','Number of Females','Number of Males'])fori,centerinenumerate(kmeans.cluster_centers_):age=center[1]# Average age for current clusterincome=center[2]# Average income for current clusterspend=center[3]# Average spending score for current clustergdf=df[df['Cluster']==i]females=gdf[gdf['Gender']==0].shape[0]males=gdf[gdf['Gender']==1].shape[0]results.loc[i]=([i,age,income,spend,females,males])results.head()
Die Ausgabe sieht folgendermaßen aus:
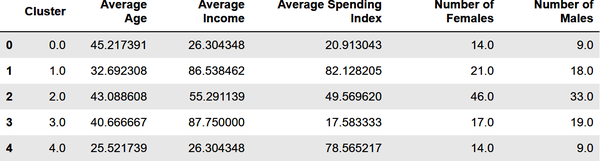
Wenn du auf dieser Grundlage Kunden mit hohem Einkommen, aber niedrigen Ausgaben für eine Werbeaktion ansprechen würdest, welche Kundengruppe (welches Cluster) würdest du wählen? Würde es einen Unterschied machen, ob du Männer oder Frauen ansprichst? Was wäre zum Beispiel, wenn du ein Treueprogramm für Kunden mit hohen Ausgaben entwickeln wolltest, dabei aber jüngere Kunden bevorzugen würdest, die vielleicht schon lange treue Kunden sind? Welche Gruppe würdest du dann ansprechen?
Eine der interessantesten Erkenntnisse, die die Clusterbildung zutage fördert, ist, dass einige der kaufkräftigsten Kunden junge Menschen (Durchschnittsalter = 25,5 Jahre) mit bescheidenem Einkommen sind. Die Wahrscheinlichkeit, dass diese Kunden weiblich sind, ist größer als die von Männern. All das sind nützliche Informationen für ein wachsendes Unternehmen, das die demografischen Gruppen, die es bedient, besser verstehen will .
Hinweis
k-means ist vielleicht der am häufigsten verwendete Clustering-Algorithmus, aber er ist nicht der einzige. Zu den anderen gehören das agglomerative Clustering, bei dem Datenpunkte hierarchisch geclustert werden, und DBSCAN, das für density-based spatial clustering of applications with noise steht. Bei DBSCAN muss die Anzahl der Cluster nicht im Voraus festgelegt werden. Es kann auch Punkte identifizieren, die außerhalb der von ihm identifizierten Cluster liegen, was nützlich ist, um Ausreißerzu erkennen - anomaleDatenpunkte, die nicht zum Rest passen. Scikit-Learn bietet Implementierungen für beide Algorithmen in seinen AgglomerativeClustering und DBSCAN Klassen.
Nutzen echte Unternehmen Clustering, um Erkenntnisse aus Kundendaten zu gewinnen? Das tun sie in der Tat. Während seines Studiums hat mein Sohn, der jetzt Datenanalyst bei Delta Air Lines ist, ein Praktikum bei einem Unternehmen für Haustierbedarf gemacht. Mit Hilfe von k-means clustering stellte er fest, dass der Hauptgrund dafür, dass Leads, die über die Website des Unternehmens eingehen, nicht in Verkäufe umgewandelt werden, die Zeitspanne zwischen dem Eingang des Leads und dem ersten Kontakt des Vertriebs mit dem Kunden ist. Daraufhin führte sein Arbeitgeber eine zusätzliche Automatisierung des Vertriebsworkflows ein, um sicherzustellen, dass die Leads schnell bearbeitet werden. Das ist unüberwachtes Lernen bei der Arbeit. Und es ist ein großartiges Beispiel dafür, wie ein Unternehmen maschinelles Lernen einsetzt, um seine Geschäftsprozesse zu verbessern.
Überwachtes Lernen
Unüberwacht Lernen ist ein wichtiger Zweig des maschinellen Lernens, aber wenn die meisten Menschen den Begriff maschinelles Lernen hören, denken sie an überwachtes Lernen. Modelle des überwachten Lernens machen Vorhersagen. Sie sagen zum Beispiel voraus, ob eine Kreditkartentransaktion betrügerisch ist oder ob ein Flug pünktlich ankommen wird. Auch sie werden mit gelabelten Daten trainiert.
Überwachtes Lernmodelle gibt es in zwei Varianten: Regressionsmodelle und Klassifizierungsmodelle. Der Zweck eines Regressionsmodells ist es, ein numerisches Ergebnis vorherzusagen, z. B. den Verkaufspreis eines Hauses oder das Alter einer Person auf einem Foto. Klassifizierungsmodelle hingegen sagen eine Klasse oder Kategorie aus einer begrenzten Menge von Klassen voraus, die in den Trainingsdaten definiert sind. Beispiele dafür sind, ob eine Kreditkartentransaktion rechtmäßig oder betrügerisch ist oder welche Zahl eine handgeschriebene Ziffer darstellt. Bei ersterem handelt es sich um ein binäres Klassifizierungsmodell, weil es nur zwei mögliche Ergebnisse gibt: Die Transaktion ist rechtmäßig oder sie ist es nicht. Letzteres ist ein Beispiel für eine Multiklassen-Klassifizierung. Da es im westarabischen Zahlensystem 10 Ziffern (0-9) gibt, gibt es 10 mögliche Klassen, für die eine handgeschriebene Ziffer stehen könnte.
Die beiden Arten von überwachten Lernmodellen sind in Abbildung 1-7 dargestellt. Auf der linken Seite geht es darum, ein x einzugeben und vorherzusagen, was y sein wird. Auf der rechten Seite geht es darum, ein x und ein y einzugeben und vorherzusagen, welcher Klasse der Punkt angehört: einem Dreieck oder einer Ellipse. In beiden Fällen besteht der Zweck der Anwendung von maschinellem Lernen darin, ein Modell für Vorhersagen zu erstellen. Anstatt dieses Modell selbst zu erstellen, trainierst du ein maschinelles Lernmodell mit markierten Daten und lässt es ein mathematisches Modell für dich entwickeln.
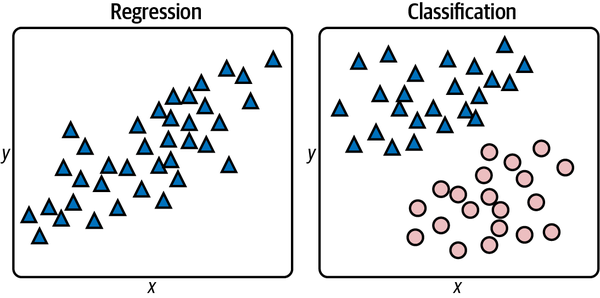
Abbildung 1-7. Regression versus Klassifizierung
Für diese Datensätze kannst du leicht mathematische Modelle erstellen, ohne auf maschinelles Lernen zurückgreifen zu müssen. Für ein Regressionsmodell könntest du eine Linie durch die Datenpunkte ziehen und die Gleichung dieser Linie verwenden, um ein y für ein x vorherzusagen(Abbildung 1-8). Bei einem Klassifizierungsmodell könntest du eine Linie ziehen, die Dreiecke und Ellipsen sauber voneinander trennt - was Datenwissenschaftler als Klassifizierungsgrenzebezeichnen - undvorhersagen, welcher Klasse ein neuer Punkt angehört, indem du feststellst, ob der Punkt über oder unter die Linie fällt. Ein Punkt knapp oberhalb der Linie wäre ein Dreieck, während ein Punkt knapp unterhalb der Linie als Ellipse klassifiziert würde.
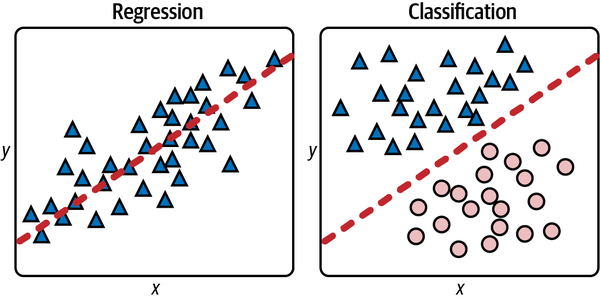
Abbildung 1-8. Regressionslinie und lineare Trennungsgrenze
In der realen Welt sind die Datensätze selten so geordnet. In der Regel sehen sie eher so aus wie in Abbildung 1-9, in der es keine einzige Linie gibt, die du ziehen kannst, um die x- und y-Werte auf der linken Seite zu korrelieren oder die Klassen auf der rechten Seite sauber zu trennen. Das Ziel ist es also, das bestmögliche Modell zu erstellen. Das bedeutet, dass du den Lernalgorithmus auswählen musst, der das genaueste Modell erzeugt.
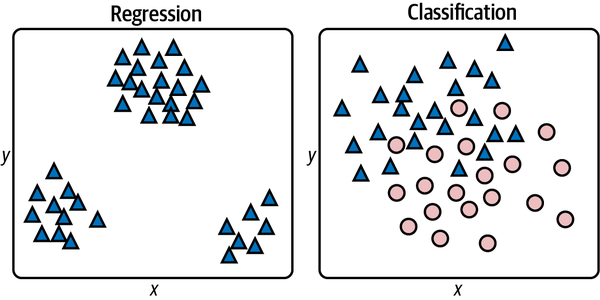
Abbildung 1-9. Datensätze aus der realen Welt
Es gibt viele Algorithmen des überwachten Lernens. Sie tragen Namen wie lineare Regression, Random Forests, Gradient Boosting Machines (GBMs) und Support Vector Machines (SVMs). Viele, aber nicht alle, können für Regression und Klassifizierung verwendet werden. Selbst erfahrene Datenwissenschaftler/innen experimentieren häufig, um herauszufinden, welcher Lernalgorithmus das genaueste Modell hervorbringt. Diese und andere Lernalgorithmen werden in den folgenden Kapiteln behandelt.
k-ächste Nachbarn
Eine der einfachsten Algorithmen des überwachten Lernens ist k-nearest neighbors. Dahinter steckt die Annahme, dass du bei einer Menge von Datenpunkten die Kennzeichnung eines neuen Punktes vorhersagen kannst, indem du die Punkte untersuchst, die ihm am nächsten liegen. Für ein einfaches Regressionsproblem, bei dem jeder Datenpunkt durch x- und y-Koordinaten charakterisiert ist, bedeutet dies, dass du bei einem x-Wert ein y vorhersagen kannst, indem du die n Punkte mit den nächstgelegenen x-Wertenfindest und den Durchschnitt ihrer y-Wertebildest. Bei einem Klassifizierungsproblem suchst du die n Punkte, die dem Punkt, dessen Klasse du vorhersagen willst, am nächsten liegen, und wählst die Klasse mit der höchsten Häufigkeit. Wenn n = 5 ist und zu den fünf nächsten Nachbarn drei Dreiecke und zwei Ellipsen gehören, dann ist die Antwort ein Dreieck, wie in Abbildung 1-10 dargestellt.

Abbildung 1-10. Klassifizierung mit k-nächsten Nachbarn
Hier ist ein Beispiel mit Regression. Angenommen, du hast 20 Datenpunkte, die beschreiben, wie viel Programmierer pro Jahr verdienen, abhängig von ihren Erfahrungsjahren. In Abbildung 1-11 sind die Erfahrungsjahre auf der x-Achse und das Jahreseinkommen auf der y-Achse aufgetragen. Dein Ziel ist es, vorherzusagen, was jemand mit 10 Jahren Erfahrung verdienen sollte. In diesem Beispiel ist x = 10, und du möchtest vorhersagen, wie hoch y sein sollte.
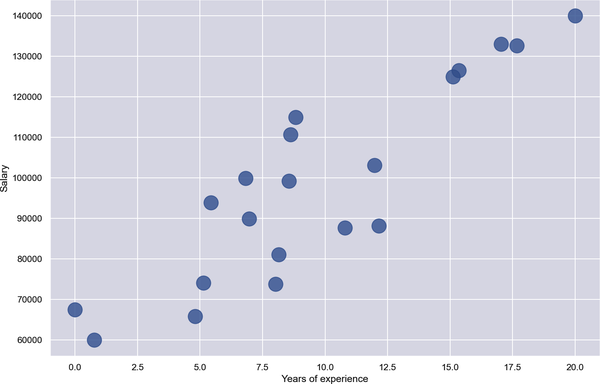
Abbildung 1-11. Gehälter von Programmierern in Dollar im Vergleich zu den Jahren der Erfahrung
Bei der Anwendung von k-nächste Nachbarn mit n = 10 werden die in Abbildung 1-12 orange markierten Punkte als die nächsten Nachbarn identifiziert - die 10 Punkte, deren x-Koordinaten x = 10 am nächsten sind . Der Durchschnitt der y-Koordinaten dieser Punkte beträgt 94.838. Daher sagt k-nearest neighbors mit n = 10 voraus, dass ein Programmierer mit 10 Jahren Erfahrung 94.838 $ verdienen wird, wie durch den roten Punkt angezeigt.
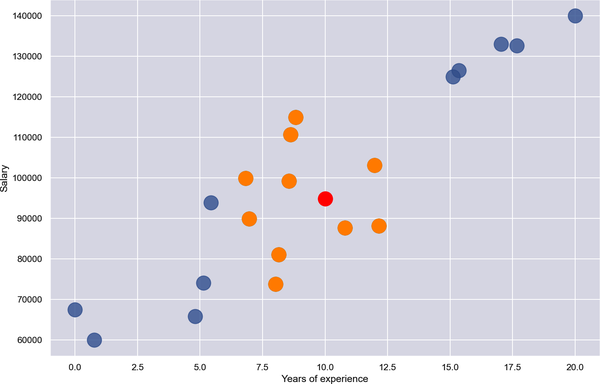
Abbildung 1-12. Regression mit k-ächsten Nachbarn und n = 10
Der Wert von n, den du bei k-ächsten Nachbarn verwendest, beeinflusst häufig das Ergebnis. Abbildung 1-13 zeigt die gleiche Lösung mit n = 5. Die Antwort fällt diesmal etwas anders aus, weil der Durchschnitt y für die fünf nächsten Nachbarn 98.713 beträgt.
In der Realität von ist die Sache etwas komplizierter, denn der Datensatz hat zwar nur eine Beschriftungsspalte, aber wahrscheinlich mehrere Merkmalsspalten - nichtnur x, sondern x1, x2, x3 und so weiter. Du kannst Abstände im n-dimensionalen Raum ganz einfach berechnen, aber es gibt verschiedene Möglichkeiten, Abstände zu messen, um die nächsten Nachbarn eines Punktes zu bestimmen, z. B. den euklidischen Abstand, den Manhattan-Abstand und den Minkowski-Abstand. Du kannst sogar Gewichte verwenden, damit nahe gelegene Punkte mehr zum Ergebnis beitragen als weit entfernte Punkte. Und anstatt die n nächsten Nachbarn zu finden, kannst du auch alle Nachbarn innerhalb eines bestimmten Radius auswählen, eine Technik, die als Radius-Nachbarn bekannt ist. Das Prinzip ist jedoch dasselbe, unabhängig von der Anzahl der Dimensionen im Datensatz, der Methode zur Abstandsmessung oder davon, ob du die n nächsten Nachbarn oder alle Nachbarn innerhalb eines bestimmten Radius auswählst: Finde Datenpunkte, die dem Zielpunkt ähnlich sind, und verwende sie, um den Zielpunkt zu regressieren oder zu klassifizieren.
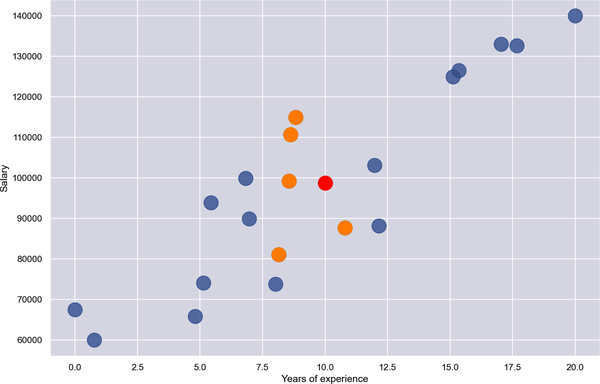
Abbildung 1-13. Regression mit k-ächsten Nachbarn und n = 5
K-Nächste Nachbarn zur Klassifizierung von Blumen verwenden
Scikit-Learn enthält Klassen namens KNeighborsRegressor und KNeighborsClassifier die dir helfen, Regressions- und Klassifizierungsmodelle mit dem Lernalgorithmus k-nearest neighbors zu trainieren. Außerdem enthält es Klassen mit den Namen RadiusNeighborsRegressor und RadiusNeighborsClassifier die einen Radius statt einer Anzahl von Nachbarn akzeptieren. Schauen wir uns ein Beispiel an, das KNeighborsClassifier verwendet, um Blumen anhand des berühmten Iris-Datensatzes zu klassifizieren. Dieser Datensatz enthält 150 Proben, die jeweils eine von drei Irisarten repräsentieren. Jede Zeile enthält vier Messwerte - Kelchblattlänge, Kelchblattbreite, Blütenblattlänge und Blütenblattbreite, alle in Zentimetern - sowie eine Bezeichnung: 0 für eine Setosa-Iris, 1 für eine Versicolor und 2 für eine Virginica. Abbildung 1-14 zeigt ein Beispiel für jede Art und verdeutlicht den Unterschied zwischen Petalen und Sepalen.

Abbildung 1-14. Iris-Datensatz (Mittleres Feld: "Blue Flag Flower Close-Up [Iris Versicolor]" von Danielle Langlois ist lizenziert unter CC BY-SA 2.5, https://creativecommons.org/licenses/by-sa/2.5/deed.en; ganz rechts: "Image of Iris Virginica Shrevei BLUE FLAG" von Frank Mayfield ist lizenziert unter CC BY-SA 2.0, https://creativecommons.org/licenses/by-sa/2.0/deed.en)
Um ein maschinelles Lernmodell zu trainieren, das anhand der Maße von Kelch- und Blütenblättern zwischen verschiedenen Irisarten unterscheidet, musst du zunächst den folgenden Code in einem Jupyter-Notebook ausführen, um den Datensatz zu laden, eine Spalte mit dem Klassennamen hinzuzufügen und die ersten fünf Zeilen anzuzeigen:
importpandasaspdfromsklearn.datasetsimportload_irisiris=load_iris()df=pd.DataFrame(iris.data,columns=iris.feature_names)df['class']=iris.targetdf['class name']=iris.target_names[iris['target']]df.head()
Der Iris-Datensatz ist einer von mehreren Beispieldatensätzen, die in Scikit enthalten sind. Deshalb kannst du ihn mit der Funktionload_iris von Scikit laden, anstatt ihn aus einer externen Datei zu lesen. Hier ist die Ausgabe des Codes:
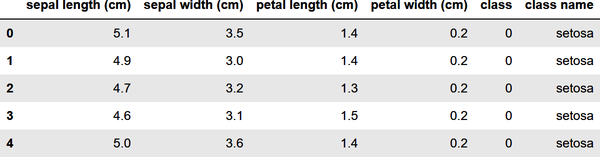
Bevor du ein maschinelles Lernmodell aus den Daten trainierst, musst du den Datensatz in zwei Datensätze aufteilen: einen zum Trainieren und einen zum Testen. Das ist wichtig, denn wenn du ein Modell nicht mit Daten testest, die es noch nie gesehen hat - also mit Daten, mit denen es nicht trainiert wurde -, weißt du nicht, wie genau es Vorhersagen machen kann.
Glücklicherweise macht es die Funktiontrain_test_split von Scikit einfach, einen Datensatz mit einem von dir festgelegten Bruchteil aufzuteilen. Verwende die folgenden Anweisungen, um einen 80/20-Split durchzuführen, bei dem 80 % der Zeilen für das Training und 20 % für die Tests reserviert sind:
fromsklearn.model_selectionimporttrain_test_splitx_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,test_size=0.2,random_state=0)
Jetzt enthalten x_train und y_train 120 Zeilen mit zufällig ausgewählten Messungen und Bezeichnungen, während x_test und y_test die restlichen 30 Zeilen enthalten. Obwohl eine 80/20-Aufteilung für kleine Datensätze wie diesen üblich ist, gibt es keine Regel, die besagt, dass du 80/20 aufteilen musst. Je mehr Daten du trainierst, desto genauer ist das Modell. (Das stimmt zwar nicht ganz, aber im Allgemeinen willst du immer so viele Trainingsdaten haben, wie du bekommen kannst.) Je mehr Daten du testest, desto sicherer kannst du die Genauigkeit des Modells einschätzen. Bei einem kleinen Datensatz ist 80/20 ein guter Ausgangspunkt.
Der nächste Schritt besteht darin, ein maschinelles Lernmodell zu trainieren. Dank Scikit sind dafür nur ein paar Codezeilen nötig:
fromsklearn.neighborsimportKNeighborsClassifiermodel=KNeighborsClassifier()model.fit(x_train,y_train)
In Scikit erstellst du ein Modell für maschinelles Lernen, indem du die Klasse instanziierst, die den von dir ausgewählten Lernalgorithmus kapselt - in diesem Fall KNeighborsClassifier. Dann rufst du fit auf, um das Modell zu trainieren, indem du es an die Trainingsdaten anpasst. Mit nur 120 Zeilen an Trainingsdaten geht das Training sehr schnell.
Der letzte Schritt von besteht darin, die 30 Zeilen der Testdaten aus dem ursprünglichen Datensatz zu verwenden, um die Genauigkeit des Modells zu messen. In Scikit wird dies durch den Aufruf der score Methode des Modells erreicht:
model.score(x_test,y_test)
In diesem Beispiel liefert score den Wert 0,966667, was bedeutet, dass das Modell in 97% der Fälle richtig lag, wenn es Vorhersagen mit den Merkmalen in x_test machte und die vorhergesagten Bezeichnungen mit den tatsächlichen Bezeichnungen in y_test verglich.
Natürlich besteht der Sinn und Zweck des Trainings eines Vorhersagemodells darin, mit ihm Vorhersagen zu treffen. In Scikit machst du eine Vorhersage, indem du die Methode predict des Modells aufrufst. Benutze die folgenden Anweisungen, um die Klasse vorherzusagen - 0 für setosa, 1 für versicolor und 2 für virginica - und die Art einer Iris zu bestimmen, deren Kelchblattlänge 5,6 cm, Kelchblattbreite 4,4 cm, Blütenblattlänge 1,2 cm und Blütenblattbreite 0,4 cm beträgt:
model.predict([[5.6,4.4,1.2,0.4]])
Die Methode predict kann mehrere Vorhersagen in einem einzigen Aufruf machen. Deshalb übergibst du ihr eine Liste von Listen und nicht nur eine Liste. Sie gibt eine Liste zurück, deren Länge der Anzahl der Listen entspricht, die du übergeben hast. Da du nur eine Liste an predict übergeben hast, ist der Rückgabewert eine Liste mit einem Wert. In diesem Beispiel ist die vorhergesagte Klasse 0, d.h. das Modell sagt voraus, dass eine Iris mit einer Kelchblattlänge von 5,6 cm, einer Kelchblattbreite von 4,4 cm, einer Blütenblattlänge von 1,2 cm und einer Blütenblattbreite von 0,4 cm höchstwahrscheinlich eine Setosa-Iris ist.
Wenn du eine KNeighborsClassifier erstellst, ohne die Anzahl der Nachbarn anzugeben, ist sie standardmäßig auf 5 eingestellt. Du kannst die Anzahl der Nachbarn auf diese Weise angeben:
model=KNeighborsClassifier(n_neighbors=10)
Versuche, das Modell erneut anzupassen (zu trainieren) und mit n_neighbors=10 zu bewerten. Erzielt das Modell dieselbe Punktzahl? Sagt predict immer noch Klasse 0 voraus? Du kannst auch mit anderen n_neighbors Werten experimentieren, um ein Gefühl für ihre Auswirkungen auf das Ergebnis zu bekommen.
Der Prozess, den hier anwendet - Daten laden, Daten aufteilen, einen Klassifikator oder Regressor erstellen, fit aufrufen, um ihn an die Trainingsdaten anzupassen, score aufrufen, um die Genauigkeit des Modells anhand von Testdaten zu bewerten, und schließlich predict aufrufen, um Vorhersagen zu treffen - ist ein Prozess, den du mit Scikit immer wieder anwenden wirst. In der realen Welt müssen die Daten häufig bereinigt werden, bevor sie für das Training und die Tests verwendet werden können. Du musst zum Beispiel Zeilen mit fehlenden Werten entfernen oder die Daten ableiten, um überflüssige Zeilen zu eliminieren. In diesem Beispiel waren die Daten bereits vollständig und gut strukturiert und mussten daher nicht weiter aufbereitet werden. .
Zusammenfassung
Maschinelles Lernen bietet Ingenieuren und Softwareentwicklern einen alternativen Ansatz zur Problemlösung. Anstatt herkömmliche Computeralgorithmen zu verwenden, um Eingaben in Ausgaben umzuwandeln, stützt sich maschinelles Lernen auf Lernalgorithmen, um mathematische Modelle aus Trainingsdaten zu erstellen. Diese Modelle werden dann verwendet, um zukünftige Eingaben in Ausgaben zu verwandeln .
Die meisten Modelle für maschinelles Lernen fallen in eine der beiden Kategorien. Unüberwachte Lernmodelle werden häufig zur Analyse von Datensätzen verwendet, indem sie Ähnlichkeiten und Unterschiede hervorheben. Sie benötigen keine markierten Daten. Überwachte Lernmodelle lernen von gekennzeichneten Daten, um Vorhersagen zu treffen - zum Beispiel, ob eine Kreditkartentransaktion rechtmäßig ist. Überwachtes Lernen kann zur Lösung von Regressions- oder Klassifizierungsproblemen eingesetzt werden. Regressionsmodelle sagen numerische Ergebnisse voraus, während Klassifizierungsmodelle Klassen (Kategorien) vorhersagen.
Dask-means Clustering ist ein beliebter unüberwachter Lernalgorithmus, während k-nearest neighbors ein einfacher, aber effektiver überwachter Lernalgorithmus ist. Viele, aber nicht alle, Algorithmen des überwachten Lernens können für Regression und Klassifizierung verwendet werden. Die Klasse KNeighborsRegressor von Scikit-Learn wendet zum Beispiel k-nearest neighbors auf Regressionsprobleme an, während KNeighborsClassifier denselben Algorithmus auf Klassifizierungsprobleme anwendet.
Pädagogen verwenden oft k-nearest neighbors, um das überwachte Lernen einzuführen, weil es leicht zu verstehen ist und in einer Vielzahl von Problembereichen recht gut funktioniert. Wenn du k-nearest neighbors beherrschst, ist der nächste Schritt auf dem Weg zum maschinellen Lernen das Kennenlernen anderer überwachter Lernalgorithmen. Das ist der Schwerpunkt von Kapitel 2, in dem verschiedene beliebte Lernalgorithmen im Zusammenhang mit der Regressionsmodellierung vorgestellt werden.
Get Angewandtes maschinelles Lernen und KI für Ingenieure now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

