Inverses and One-to-One Functions
Let’s consider the following two functions.
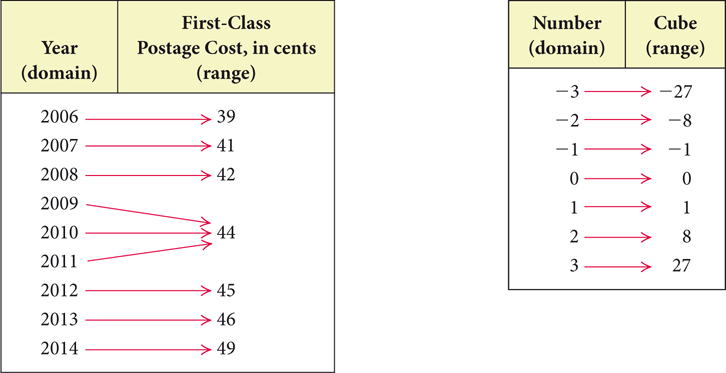
Source: U.S. Postal Service
Suppose we reverse the arrows. Are these inverse relations functions?
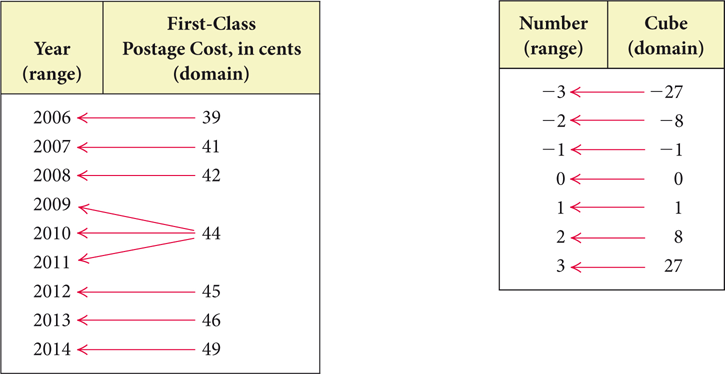
Source: U.S. Postal Service
We see that the inverse of the postage function is not a function. Like all functions, each input in the postage function has exactly one output. However, the output for 2009, 2010, and 2011 is 44. Thus in the inverse of the postage function, the input 44 has three outputs, 2009, 2010, and 2011. When two or more inputs of a function have the ...
Get Algebra and Trigonometry, 5th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

