17.1 Complex Numbers
INTRODUCTION
You have undoubtedly encountered complex numbers in your earlier courses in mathematics. When you first learned to solve a quadratic equation ax2 + bx + c = 0 by the quadratic formula, you saw that the roots of the equation are not real, that is, complex, whenever the discriminant b2 − 4ac is negative. So, for example, simple equations such as x2 + 5 = 0 and x2 + x + 1 = 0 have no real solutions. For example, the roots of the last equation are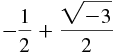 
and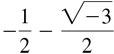 
. If it is assumed that , then the roots are written and .
Get Advanced Engineering Mathematics, 7th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
