Fluent Python: The Power of Special Methods
You’ve used Python for years. Do you really know it? Be brave and skin that Python. In this cut, Luciano Ramalho probes deep into special methods and the Data Model. Become fluent with idiomatic Python.
 Fluent Python - Luciano Ramalho (source: O'Reilly)
Fluent Python - Luciano Ramalho (source: O'Reilly)
Fluent Python: The Data Model
If you learned another object-oriented language before Python, you may have found it strange to call len(collection) instead of collection.len(). This apparent oddity is the tip of an iceberg that, when properly explored, is the key to everything we call Pythonic. The iceberg is called the Python data model, and it describes the API that you can use to make your own objects play well with the most idiomatic language features.
To create pleasant, intuitive, and expressive libraries and APIs, you need to leverage the Python data model, so that your objects behave consistently with the built-in objects in the language.
Special Methods
The data model defines a set of interfaces. Python is a dynamically typed language, so to implement an interface you just code methods with the expected names and signatures. You are not required to fully implement an interface if a partial implementation covers your use cases. The data model interfaces all use method names prefixed and suffixed with __ (two underscores), such as __add__ or __len__. These are known as special methods, magic methods or dunder methods (after double underscore).
Your code will rarely invoke special methods. Instead, you’ll implement special methods that the Python interpreter will call when handling syntax for:
- Iteration
- Collections
- Attribute access
- Operator overloading
- Function and method invocation
- Object creation and destruction
- String representation and formatting
- Managed contexts (i.e., with blocks)
To see the data model in action, we’ll implement a subset of the sequence interface, which describes the behavior of strings, lists, tuples, arrays, and many other Python types. Our second example will cover operator overloading.
A Pythonic Card Deck
To experiment with special methods, we’ll code a package to represent decks of playing cards. First, we’ll create a simple class to represent an individual card.
The Card Class
A card will be a record with two data attributes and no methods. Python has a factory to make such simple classes: collections.namedtuple.
import collections
Card = collections.namedtuple('Card', ['rank', 'suit'])
Note that the namedtuple factory takes two arguments: the name of the class to create and a sequence of attribute names.
The Card class can then be instantiated as usual:
beer_card = Card('7', 'diamonds')
beer_card
If we inspect the attributes of the Card class, we see lots of special methods. Among them, __repr__ is the one that produces the string representation we just saw.
dir(Card)
The __repr__ method is invoked implicitly by the console and debugger, or explicitly by the repr() built-in function.
The output of repr() for a Card instance is so explicit that you can clone a card by applying eval() to its repr():
my_card = eval(repr(beer_card)) my_card == beer_card
We are now ready to code the class to represent a deck of cards.
The FrenchDeck Class
I’ll call the class for a collection of cards FrenchDeck, since that is the formal name of the set of 52 cards with 4 suits, used not only in France, but in most of the Western world. Its code is short but it does a lot, as you’ll soon see.
class FrenchDeck:
ranks = [str(n) for n in range(2, 11)] + list('JQKA')
suits = 'spades diamonds clubs hearts'.split()
def __init__(self):
self._cards = [Card(rank, suit) for suit in self.suits
for rank in self.ranks]
def __len__(self):
return len(self._cards)
def __getitem__(self, position):
return self._cards[position]
The trickiest part is the use of a list comprehension in the initializer to build a list of cards by computing the Cartesian product of the lists of suits and ranks. The logic of that list comprehension is explained in Chapter 2 of Fluent Python, but right now we want to focus on the external behavior of the class, not its implementation, so please believe that self._cards holds a list of 52 Card instances.
deck = FrenchDeck() len(deck)
The len built-in function knows how to handle a FrenchDeck because we implemented the __len__ special method. This is consistent with how built-in collections work, and saves the user from memorizing arbitrary method names for common operations (“How to get the number of items? Is it .length(), .size() or what?”).
The __getitem__ special method supports the use of [] and provides a lot of functionality.
We can get any card by index, as usual. For example, first and last:
deck[0], deck[-1]
We can also use slice notation to retrieve a subset of the cards:
deck[:3]
Here’s how to use the the third parameter of a slice to get just the aces in the deck by starting at card index 12 and skipping 13 cards from that point onwards.
deck[12::13]
The in operator also works with our FrenchDeck instances. This behavior can be optimized by implementing a __contains__ method, but if you provide a __getitem__ method, Python is smart enough to scan the collection from item 0 to the end.
Card('Q', 'hearts') in deck
Card('Z', 'clubs') in deck
Iteration
Our card decks are also iterable. Implementing an __iter__ method to return a custom iterator is the optimal way to achieve this. But, as a fallback, Python knows how to iterate over any collection that implements __getitem__ and accepts integer indexes starting at 0:
for card in deck:
print(card)
By supporting iteration, we can leverage many functions in the standard library that work with iterables, like enumerate(), reversed(), as well as the constructor for list and several other collection types.
list(enumerate(reversed(deck), 1))
Another powerful function that works with iterables is sorted. It builds a sorted list from iterables that generate a series of comparable values.
sorted(deck)
We can define custom sorting criteria by implementing a function to produce a key from each item in the series, and passing it as the key= argument to sorted. Here is a function that implements the “spades high” ordering, where cards are sorted by rank, and within each rank, spades is the highest suit, followed by hearts, diamonds, and clubs:
def spades_high(card):
rank_value = FrenchDeck.ranks.index(card.rank)
return (rank_value, card.suit)
As written, spades_high produces the highest key value for the Ace of spades and the lowest for the 2 of clubs:
spades_high(Card('A', 'spades')), spades_high(Card('2', 'clubs'))
sorted(deck, key=spades_high)
Shuffling and Item Assignment
The standard library provides many functions that operate on sequences. For example, picking a random item is as simple as this:
import random random.choice(deck)
This is a live notebook, so each time you run the code above, the random choice will be computed again, producing different results.
How about shuffling? Let’s try it next.
try:
random.shuffle(deck)
except TypeError as e: # this error is expected!
print(repr(e))
else:
print('The deck was shuffled!')
The first time you run this notebook you should see the exception above: TypeError: 'FrenchDeck' object does not support item assignment. The problem is that random.shuffle works by rearranging the items in place, but it can only do deck[i] = card if the sequence implements the __setitem__ method.
Monkey Patching
We could redefine the whole FrenchDeck class here, but let’s do a monkey patch, just for fun. Monkey patching is changing classes or modules at run time. To enable shuffling, we can create a function that puts a card in a certain position of a deck:
def put(deck, index, card):
deck._cards[index] = card
Note how put is tricky: it assigns to the “private” attribute deck._cards. Monkey patches are naughty. They often touch the intimate parts of the target objects.
Now we can patch the FrenchDeck card to insert the put function as its __setitem__ method:
FrenchDeck.__setitem__ = put
Now we can shuffle the deck and get the first five cards to verify:
random.shuffle(deck) deck[:5]
Again, in a live notebook such as this, each time you run the cell above you should get a different result.
If you want to disable item assignment to experiment further, you can delete __setitem__ from the FrenchDeck class. Then random.shuffle will stop working. Uncomment and run the next cell to try this.
# del FrenchDeck.__setitem__ # random.shuffle(deck) # <-- this will break
Monkey patching has a bad reputation among Pythonistas. Monkey patches are often tightly bound to the implementation details of the patched code, so we apply them only as a last resort.
However, some important Python projects use this technique to great effect. For example, the gevent networking library, uses monkey patching extensively to make the Python standard library support highly concurrent network I/O.
Here, monkey patching was a didactic device to illustrate these ideas:
- Classes are objects too, so you can add attributes to them at run-time
- Methods are merely functions assigned to class attributes
- What makes a method “special” is naming. Python recognizes a fixed set of special method names, such as
__setitem__ - Many standard operations are implemented by special methods. For example, getting and setting items in sequences triggers the
__getitem__and__setitem__methods
Most of the special method names supported by Python are in the data model chapter of the Python Language Reference.
What We Saw So Far
The FrenchDeck example demonstrates how smart use of Python features lets us go very far with just a little coding.
FrenchDeck implicitly inherits from object. All its interesting behaviors are not inherited, but come from leveraging the data model and composition. The __len__ and __getitem__ methods delegate all the work to a list object, self._cards. Note that my code never calls special methods directly. They are called by the interpreter.
By implementing the special methods __len__ and __getitem__, our class behaves like a basic Python sequence, allowing it to benefit from core language features such as:
- The
len()built-in function - Item access
- Slicing
- Iteration
- Many functions that accept sequences or iterables (e.g.
list,enumerate,sorted,random.choice)
By adding __setitem__, the deck became mutable, thus supporting random.shuffle. When I first wrote this example years ago I actually did implement a FrenchDeck.shuffle method. But then I realized that I was already coding a sequence-like object, so I should just use the existing sequence shuffling function in the standard library.
The main point is this: if you follow the conventions of the data model, your users can take more advantage of the standard library. So your objects will be easier to use and more powerful at the same time.
The next example will show how special methods are used for operator overloading.
Overloading Operators for Vector Arithmetic
Programmers often think of a vector as a synonym for array, but let’s consider Euclidean vectors used in math and physics, like these:
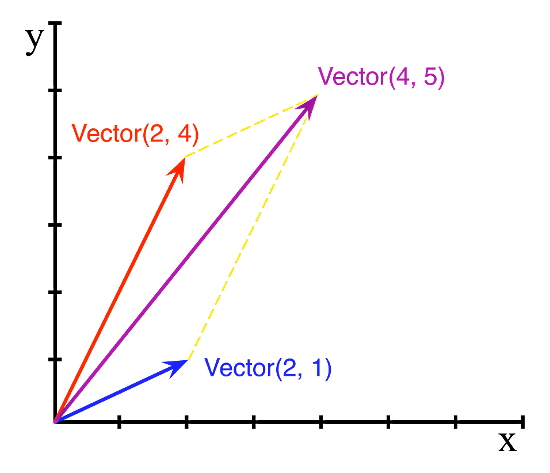
The picture above illustrates a vector addition. We’d like to represent those objects in code, like this:
v1 = Vector([2, 4]) v2 = Vector([2, 1]) v3 = v1 + v2 print(v3) # --> Vector([4, 5])
Let’s start with the basic methods every object should have: __init__ and __repr__.
Please note this is a didactic example only!
In practice, to do numerical computations with vectors and matrices, you should use NumPy and other packages from the SciPy collection.
Vector Take #1: Initialization and Inspection
Our first step enables building and inspecting instances of vector. We’ll use an array of doubles to store the arguments passed to the constructor:
from array import array
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
Like the standard Python console and debugger, iPython uses repr(v1) to render a v1 object, triggering a call to v1.__repr__():
v1 = Vector([2, 4, 6]) v1
The first line of the __repr__ method uses a generator expression to iterate over the array of floats to render each as a string, then joins them with commas. The second line builds a string with the name of the class (eg. 'Vector()') and the components string inside the parenthesis, emulating the syntax of a constructor call with a list argument.
Insight: why
reprand__repr__,lenand__len__?You may be wondering why we say that Python calls
reprbut we implement__repr__. With theFrenchDeckit was the same thing: we saw thatlen(deck)resulted in a call todeck.__len__().There is a practical reason: for built-in types, a call such as
len(obj)does not invokeobj.__len__(). If the type ofobjis a variable length built-in type coded in C, its memory representation has a struct namedPyVarObjectwith anob_sizefield. In that case,len(obj)just returns the value of theob_sizefield, avoiding an expensive dynamic attribute lookup and method call. Only ifobjis a user defined type, thenlen()will call the__len__()special method, as a fallback.A similar rationale explains why Java arrays have a
.lengthattribute, while most Java collections implement.length()or.size()methods. The difference is that Python strives for consistency; it optimizes the operation of the fundamental built-in types, but allows our own types to behave consistently by implementing the special methods defined in the data model.
Vector Take #2: Iteration
As mentioned, the recommended way to make an iterable object is to implement an __iter__ method that returns an iterator.
from array import array
import math
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
def __iter__(self): # <- - - - - - - - - - - new method
return iter(self._components)
Here I just call the iter() built-in on the _components array to get an iterator that will return each component of the vector. As a result, here are some things we can do with vector instances now:
v3 = Vector([10, 20, 30]) x, y, z = v3 # tuple unpacking x, y, z
list(v3), set(v3) # seed collection constructors
for label, value in zip('xyz', v3): # parallel iteration with zip
print(label, '=', value)
By the way, did you know that the zip built-in function has nothing to do with compressed files?
The Pythonic
zipThe
zipfunction is named after the zipper fastener. The fastener works by interlocking pairs of teeth taken from both zipper sides, a good visual analogy for whatzip(left, right)does: producing tuples of items to allow parallel iteration over two or more collections.
Understanding
zipis a small but important step to becoming a fluent Pythonista. Likeenumerateandreversed,zipis often used inforloops to support use cases that would require error-prone index manipulations in a language like C. Python’sforloop prevents many bugs by handling the index for you and producing the items you actually want. Most Python code I’ve seen that explicitly manipulated indexes inforloops could be written more readably and safely using one or more of these functions. In Python 3,zip,enumerate, andreversedreturn generators, so they are memory-efficient and fast.
Vector Take #3: map-reduce and abs
Now that Vector is iterable, we can easily compute its absolute value using the Euclidean norm. The formula is a generalization of the Pythagorean theorem:
We can code the sum inside the square root using the map-reduce functional programming pattern. In the map stage we compute the square of each vector component, and in the reduce stage we add them up.
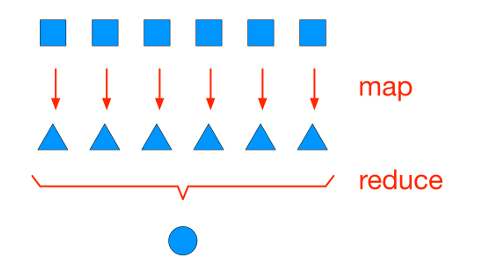
Here is one way, using map with lambda to compute the squares, then sum:
v = Vector([3, 4]) sum(map(lambda x: x*x, v))
That works. But the most idiomatic way in modern Python is using a generator expression instead of map and lambda:
sum(x*x for x in v)
Isn’t that elegant?
Computing the square root of that sum, we have our __abs__ method:
from array import array
import math
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
def __iter__(self):
return iter(self._components)
def __abs__(self): # <- - - - - - - - - - - new method
return math.sqrt(sum(x * x for x in self))
Now we can use the abs() built-in to compute the absolute value of a vector, just like we use it with other numeric types:
abs(5), abs(-5.0), abs(3+4j), abs(Vector([3,4]))
Vector Take #4: Scalar Multiplication
Scalar multiplication is the product of a vector and a real number. Given a vector v, the expression v*x builds a new vector with each component multiplied by x. Here’s how to do it using a generator expression:
v5 = Vector([1, 2, 3, 4, 5]) x = 11 Vector(x * y for y in v5)
To overload the * operator we start by implementing a __mul__ method, like this:
from array import array
import math
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
def __iter__(self):
return iter(self._components)
def __abs__(self):
return math.sqrt(sum(x * x for x in self))
def __mul__(self, y): # <- - - - - - - - - - - new method
return Vector(x * y for x in self)
We can now test it:
Vector([1, 2, 3, 4, 5]) * 11
All seems good, but there is a problem. Look what happens if we multiply a number by a vector:
try:
res = 11 * Vector([1, 2, 3, 4, 5])
except TypeError as e:
print(repr(e))
else:
print('OK! result:', res)
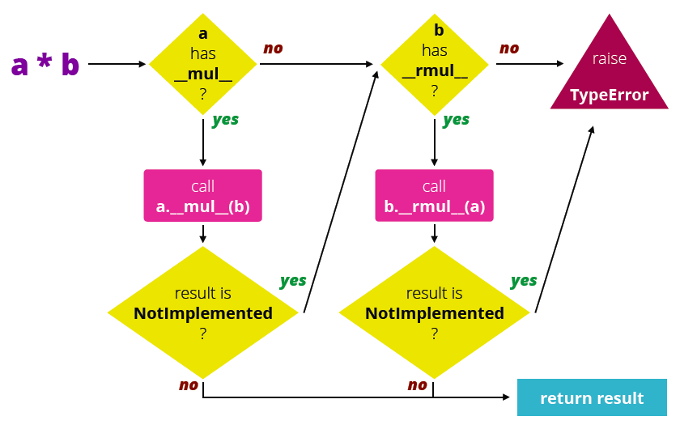
The problem is that the __mul__ method in the int class doesn’t know how to handle vectors. How could it? We just made up this Vector class. The solution to this problem is a pattern named double dispatch, which Python implements at the interpreter level using special operator method names. See the picture below.
Double Dispatch
To evaluate
a*b, Python checks ifa.__mul__(b)exists. If it doesn’t, or if it returns the special valueNotImplemented, then Python callsb.__rmul__(a). Note thatNotImplementedis not an exception, but a special value that operator overloading methods return to say “I can’t handle that operator.” Many operator overloading special methods have a sibling named with thatrprefix, like__rmul__,__radd__, etc. Therprefix stands for reversed.If the forward operator method is absent or returns
NotImplemented, then Python invokes the reversed operator, swapping the operands. Now if the reversed operator method is absent or returnsNotImplemented, the interpreter raises aTypeErrorexception stating that the operands are invalid.
Now we know what to do to fix that bug. Here’s the code of Vector with the __rmul__ method:
from array import array
import math
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
def __iter__(self):
return iter(self._components)
def __abs__(self):
return math.sqrt(sum(x * x for x in self))
def __mul__(self, y):
return Vector(x * y for x in self)
def __rmul__(self, y): # <- - - - - - - - - - - new method
return self * y
Let’s prove it works:
11 * Vector([1, 2, 3, 4, 5])
By design, scalar multiplication is a commutative operation between a vector and a scalar number.
However, as implemented, our __mul__ method raises confusing exceptions if the non-vector operand is unsuitable:
try:
res = Vector([10, 11, 12]) * 'spam'
except TypeError as e:
print(repr(e))
else:
print('OK! result:', res)
The problem with this exception is the message; it mentions a 'float' but the user code only shows a Vector and a str — the fact that vector stores components as floats is an implementation detail. What we see here is the exception raised by multiplying x * y where x is one of the components of the array and y is the string 'spam'. We need to handle this exception ourselves to provide better error reporting.
At first, it may seem reasonable to check the type of the y argument in __mul__ and raise an exception if we can’t handle that type. However, there are several scalar numeric types in the standard library, from plain int to Fraction, and external libraries like NumPy define even more numeric types.
When overloading operators we should not raise type exceptions most of the time. Instead, we return NotImplemented to let the double dispatch algorithm continue, giving the other operand a chance to perform the multiplication in its __rmul__ method — if it can.
Duck Typing FTW
The Pythonic approach here is to use duck typing; we avoid type checking and rely on implemented behavior. In this case, the y argument will multiply each floating point number in the _components array, so any y is good enough as long as it supports multiplication by a float. If that fails, we return NotImplemented. Here is the code to do that:
from array import array
import math
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
def __iter__(self):
return iter(self._components)
def __abs__(self):
return math.sqrt(sum(x * x for x in self))
def __mul__(self, y): # <- - - - - - - - - - - improved method
try:
return Vector(x * y for x in self)
except TypeError:
return NotImplemented
def __rmul__(self, y):
return self * y
Now we have behavior that is compatible with the double dispatch mechanism, and Python can raise a TypeError with a more sensible message:
try:
res = Vector([10, 11, 12]) * 'spam'
except TypeError as e:
print(repr(e))
else:
print('OK! result:', res)
Can you explain why the message mentions “sequence” first, even if the test expression was Vector([10, 11, 12]) * 'spam'? Following the double dispatch diagram may be helpful.
We had to handle a few issues to overload *, but now our implementation is smart enough to get a correct result from multiplying a fraction and a vector, thanks to the power of duck typing:
from fractions import Fraction Fraction(1, 3) * Vector([10, 20, 30])
Vector Take #5: Vector Addition
Now let’s tackle vector addition: that is an operation on two vectors which returns a new vector made from the pairwise addition of the components of the operands, like this:
v1 = Vector([10, 11, 12, 13]) v2 = Vector([32, 31, 30, 29]) v3 = v1 + v2 print(v3) # --> Vector([42, 42, 42, 42])
That parallel addition is a perfect task for the zip function, but there is a caveat, as soon as one of its iterable arguments is exhausted, zip silently stops producing tuples:
list(zip([1, 2, 3, 4], [10, 20]))
In our case, that behavior would ignore extra components from the longer vector operand. A more useful behavior would be to produce a vector as long as the longest operand by padding the shortest one with zeroes.
Fortunately the itertools module has the solution, the aptly named zip_longest generator function:
import itertools list(itertools.zip_longest([1, 2, 3, 4], [10, 20], fillvalue=0))
The final listing shows the __add__ method using zip_longest and basic error handling in line with the double dispatch pattern. I went ahead and implemented the __radd__ method as well:
from array import array
import math
import itertools
class Vector:
def __init__(self, components):
self._components = array('d', components)
def __repr__(self):
components_str = ', '.join(str(x) for x in self._components)
return '{}([{}])'.format(self.__class__.__name__, components_str)
def __iter__(self):
return iter(self._components)
def __abs__(self):
return math.sqrt(sum(x * x for x in self))
def __mul__(self, y):
try:
return Vector(x * y for x in self)
except TypeError:
return NotImplemented
def __rmul__(self, y):
return self * y
def __add__(self, other): # <- - - - - - - - - - - new method
try:
pairs = itertools.zip_longest(self, other, fillvalue=0)
return Vector(x + y for x, y in pairs)
except TypeError:
return NotImplemented
def __radd__(self, other): # <- - - - - - - - - - - new method
return self + other
The way I implemented the + operator you can add a vector with any iterable that produces numbers — the result will always be a vector:
Vector([1, 2, 3, 4]) + [100, 200, 300]
Python does not allow adding tuples and lists. But the meaning of vector addition is very different; we are not concatenating a whole structure to another, but we are reading individual components from the operands to create a new vector.
I am not certain that the behavior I implemented is desirable. But it’s an interesting demonstration of the power of duck typing.
Conclusion
These short examples demonstrate the power of the Python data model. We saw how:
- Basic language syntax like
o[i]anda + bhandle user-defined types via special methods - Implementing just
__len__and__getitem__is enough to get a usable sequence type, and then leverage many standard library functions such assorted,choiceandshuffle - Non-sequence types can provide an
__iter__method to become iterable, enabling the use of powerful built-ins likesumandzip, as well as memory efficient generator expressions and the many specialized generator functions from theitertoolsmodule - Infix operators like
+and*are supported by methods like__add__and__mul__, with reversed operator methods (e.g.__radd__) to allow flexible handling of mixed types through double dispatch
These are only some examples of special methods usage. Other functionality, such as properties, context managers, and class metaprogramming also rely on special methods defined in the Python data model.